迭代法求解线性方程组_李锐博恩的博客-CSDN博客_迭代法解线性方程组

MATLAB代码：基于MATLAB的三母线高斯赛德尔潮流分析计算 关键词：潮流计算 电力系统 高斯赛德尔迭代法 MATLAB 参考文献+自制详细实验文档 仿真平台：MATLAB 主要内容：潮流计算是判断电力系统是否稳定的重要方法，通过最初赋予的初始条件来进行计算系统的当前状态，分析结果对于电力系统的维护非常的重要。 本文通过介绍电力系统稳定运行和电力系统潮流分析的基本情况来拉开对潮流分析计算的帷幕

高斯-赛德尔迭代法的代码实现 function x=agui_GS(a,b)n=length(b);N=100;e=10^(-4);x0=zeros(n,1);x=x0;x0=x+2*e;k=0;a1=tril(a);a2=inv(a1);while norm(x0-x,inf)>e&k<Nk=k+1;x0=x;x=-a2*(a-a1)*x0+a2*b;format l

约德尔测试 题目描述 兰博和提莫闲聊之后，回归到了他们的正题，约德尔人的未来。 说起约德尔人的未来，黑默丁格曾经提出了一个约德尔测试，将约德尔人的历史的每个阶段都用一个字符表达出来。(包括可写字符,不包括空格。)。然后将这个字符串转化为一个01串。转化规则是如果这个字符如果是字母或者数字，这个字符变为1,其它变为0。然后将这个01串和黑默丁格观测星空得到的01串做比较，得到一个相似率。相似率

线性方程组的迭代解法 2024年1月1日 #analysis 文章目录 线性方程组的迭代解法基本迭代法Jacobi迭代高斯-赛德尔（GS）迭代SOR迭代 迭代的收敛性分析和误差估计下链 基本迭代法 Jacobi迭代 A = D − L − U A=D-L-U A=D−L−U D x ( k + 1 ) = ( L + U ) x ( k ) + b Dx^{

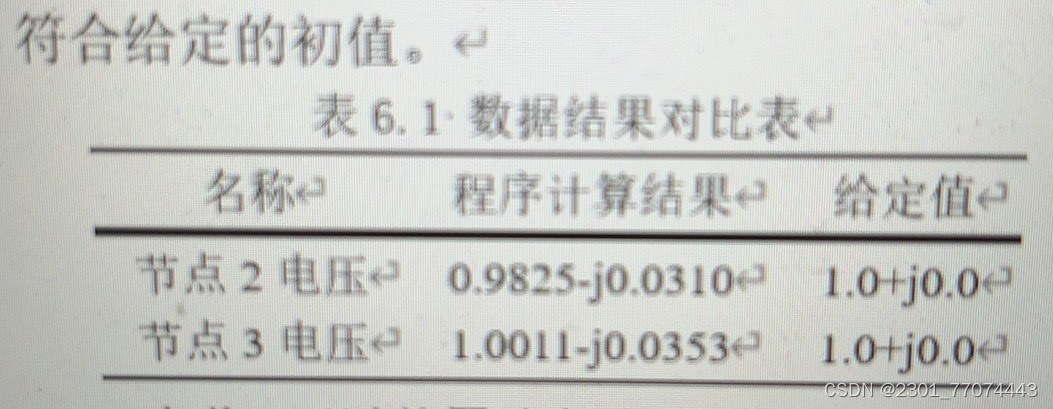
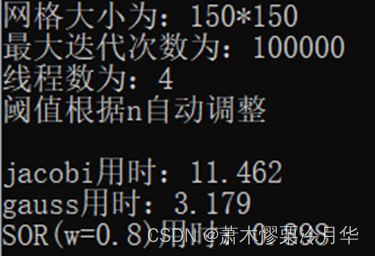
稳态导热，稳态导热是物体的温度不随时间而变化的导热过程。稳态热传导问题在这里被模拟为，对于一个n*n的网格，对其某个位置持续给定初始温度，求解最终的稳态导热状态，稳态热传导问题即求解最终的稳态温度。 温度网格示例如下： 正确解决温度热传导问题后得到的温度图像类似于下图所示： 问题拟定 对于n*n的网格，初始温度全部为0，给其上边与右边的中部位置持续给定大小为1的热度，

近日，创新电器品牌德尔玛（广东德尔玛科技股份有限公司，代码“301332”），正式登陆深圳证券交易所创业板，发行价格为14.81元/股。上市前，德尔玛已完成了5亿元A轮融资及3.3亿元A+轮融资，投资方包括中信产业基金、弘章资本、欧派家居等。 对于资本而言，德尔玛深耕的智能小家电领域极具爆发潜力。根据Euromonitor数据，国内小家电市场规模（不含净水类）从2016年的3363.7亿元增长至

算法流程 其实迭代法前面已经学习过啦，这里的迭代是在前面迭代的基础上的高阶形式——即解决线性方程组的问题。 下面简单介绍雅克比迭代的基本流程。 雅可比迭代 有一线性方程组， A x = b Ax=b Ax=b,其中： 我们可以将其化为以下形式： x i = B x j + f , ( i = 1 , 2 , 3...... n , j = 1 , 2 , 3 , ¬ i . . . .