逐次专题
逐次代入法求解非线性方程
//用逐次代入法求解非线性方程 #include <iostream> #include <math.h> #include <process.h> using namespace std; class successive { private: int iteration; double eps, error, f, x_new, x_old; public: successive(
TSP问题之二边逐次修正法
TSP问题之二边逐次修正法 算法步骤算法代码例题1(无向图)例题2(有向图) 算法步骤 算法代码 原算法只支持无向图,以下代码同时支持无向图和有向图。 import numpy as npdef ebzcxz(D, H):# 计算初始H圈权值W = 0for i, j in zip(H, H[1:] + [H[0]]):W += D[i, j]print('初始H圈为
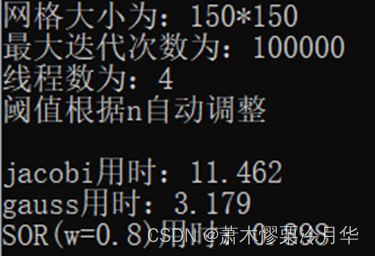
C++多线程下分别使用雅各比迭代法、高斯赛德尔迭代法、逐次超松弛迭代法解决稳态热传导问题,使用Python数据可视化
稳态导热,稳态导热是物体的温度不随时间而变化的导热过程。稳态热传导问题在这里被模拟为,对于一个n*n的网格,对其某个位置持续给定初始温度,求解最终的稳态导热状态,稳态热传导问题即求解最终的稳态温度。 温度网格示例如下: 正确解决温度热传导问题后得到的温度图像类似于下图所示: 问题拟定 对于n*n的网格,初始温度全部为0,给其上边与右边的中部位置持续给定大小为1的热度,
(13)幂模m与逐次平方法
逐次平方法 如何计算 5 100 000 000 000 000 ( m o d 12 830 603 ) 5^{100\ 000\ 000\ 000\ 000}(\mod 12\ 830\ 603) 5100 000 000 000 000(mod12 830 603) 呢?如果12830603是素数,你会设法使用费马小定理,即使不是素数,也可以利用欧拉公式。事实上, 12 8
逐次变分模态分解(Sequential Variational Mode Decomposition,SVMD)(附代码)
代码原理 逐次变分模态分解(Sequential Variational Mode Decomposition,SVMD)是一种用于信号处理和数据分析的方法。它可以将复杂的信号分解为一系列模态函数,每个模态函数代表了信号中的一个特定频率成分。SVMD的主要目标是提取信号中的不同频率成分,并将其重构为原始信号。 SVMD的基本原理是通过变分模态分解的方式将信号分解为多个模态函数。在每个迭代步骤中
Aitken(埃特金)逐次插值法 | 一次插值、二次插值、k次插值
Aitken(埃特金)逐次插值法 判断离散数据 ( x i , y i ) ( i = 0 , 1 , 2 , ⋯ , n ) (x_i,y_i)(i=0,1,2,\cdots,n) (xi,yi)(i=0,1,2,⋯,n)的插值精度,既可以采用事后误差估计的方法,也可以在插值点x的附近选取部分数据进行插值,然后再增加一些插值节点进行插值。若两次的插值结果之差小于规定的误差,则可认为插值精度
基于逐次凸近似(Successive Convex Approximation)的非凸二次规划问题求解---MATLAB程序
本文引用了上海财经大学崔雪婷老师最优化理论与方法课程,课程链接如下: 【最优化理论与方法-第十二讲-二次规划】 https://www.bilibili.com/video/BV1vQ4y1P77A/?p=4&share_source=copy_web&vd_source=ec4b99096a4967b6330aae8eaef5e99b 崔老师讲最优化讲的特别好!满分推荐! 逐次凸近似(Su