二阶差分题单

本文主要是介绍二阶差分题单，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原理

差分与前缀和互为逆运算，故将二阶差分数组进行两次前缀和操作得到结果。

下面我们用一个例子理解:

原差分数组

i	0	1	2	3	4	5	6	7	8	9
a[i]	1	0	0	1	0	0	0	0	0	0

一次前缀和操作后的数组

i	0	1	2	3	4	5	6	7	8	9
a[i]	1	1	1	2	2	2	2	2	2	2

两次前缀和操作后的数组

i	0	1	2	3	4	5	6	7	8	9
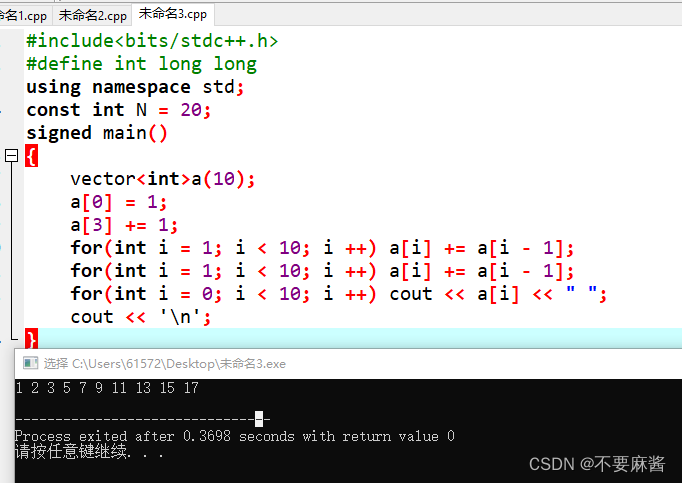
a[i]	1	2	3	5	7	9	11	13	15	17

                可以看到两次前缀和数组结果中，

                0 <= i <= 2序列①结果为 1 2 3，形成公差 d = 1 的等差数列

                3 <= i <= 9序列②结果为 5 7 9 11 13 15 17，形成公差 d = 2 的等差数列

                这是因为 原数组中 a[0] = 1, a[3] = 1。一次前缀和后序列①的每个数都变为了 1，

                序列②的每个数都变为了 2。再进行一次前缀和后序列①内相邻的两个数相差 1，

                序列②内相邻的两个数相差 2。

同理推广，二阶差分是一个公差叠加的过程，即对原数组的某个数操作就是改变以从当前数开头的序列的公差。

总结起来：

我们想要得到区间为 [l, r] ，公差为 d 等差序列 d, 2 * d, ... , d * (r - l)，

只需a[l] += d, a[r + 1] = -d，再进行两次前缀和。

想要得到区间为 [l, r] ，以 x 为首项，公差为 d 等差序列 x + d, x + 2 * d, ... , x + d * (r - l)。

那么可以做以下操作 ①a[l] += x, a[l + 1] += -x。②a[l] += d, a[r + 1] = -d。③两次前缀和

题目

 绝世武功（板子题）

#include <bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{int n, m, ans = 0; cin >> n >> m;vector<int>a(n + 1);for(int i = 1; i <= m; i ++){int  l, r, s, e; cin >> l >> r >> s >> e;int d = (e - s) / (r - l);a[l] += s;a[l + 1] += (d - s);a[r + 1] += (-e - d);a[r + 2] += e;}for(int i = 1; i <= n; i ++) a[i] += a[i - 1];for(int i = 1; i <= n; i ++) a[i] += a[i - 1];for(int i = 1; i <= n; i ++) ans += a[i];//, cout << a[i] << " ";// cout << '\n';cout << ans << '\n';return 0;
}

P8811 [蓝桥杯 2022 国 C] 六六大顺（高精度 + 二阶差分）

观察到111 x 111 = 12321，两个等差序列可以用二阶差分解决

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 25;signed main()
{	ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n; cin >> n;int mx = 2e7 + 10;vector<int>a(mx);for(int i = 1; i <= n; i ++){a[1] += 36;a[i + 1] -= 2 * 36;a[2 * i + 1] += 36;}for(int i = 1; i <= 2 * n + 1; i ++) a[i] += a[i - 1];for(int i = 1; i <= 2 * n + 1; i ++) a[i] += a[i - 1];int t = 0;int cnt = 0;for(int i = 1; i < mx; i ++){a[i + 1] += a[i] / 10;a[i] %= 10;if(a[i]) cnt = i;}for(int i = cnt; i >= 1; i --) cout << a[i];cout << '\n';
}

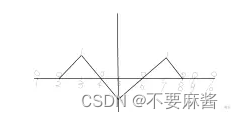
P5026 Lycanthropy（二阶差分）

等差数列变化图，直接上二阶差分

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 25; 
signed main()
{	ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n, m; cin >> n >> m;vector<int>a(2e6 + 10);int da = 40010;for(int i = 1; i <= n; i ++){int v, x; cin >> v >> x;a[x - 3 * v + 1 + da] += 1;a[x - 2 * v + 1 + da] += -2;a[x + 1 + da] += 2;a[x + 2 * v + 1 + da] += -2;a[x + 3 * v + 1 + da] += 1;}for(int i = 1; i <= 2e6; i ++) a[i] += a[i - 1];for(int i = 1; i <= 2e6; i ++) a[i] += a[i - 1];for(int i = 1; i <= m; i ++) cout << a[i + da] << " ";cout << '\n';
}

这篇关于二阶差分题单的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---