本文主要是介绍second order system analysis 自动控制原理 二阶系统的matlab仿真分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
二阶系统的matlab仿真分析
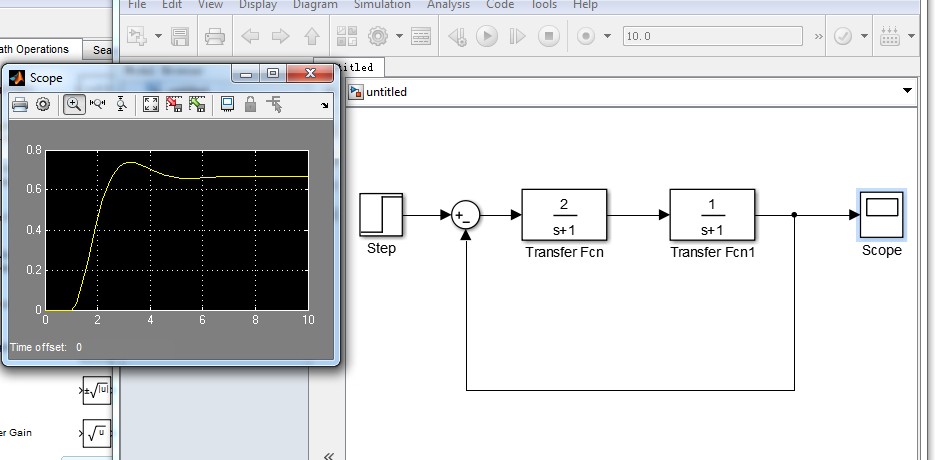
二阶系统的matlab仿真分析如上图。
根据二阶函数对阶跃函数的响应函数,我们对参数epsilon进行分析讨论
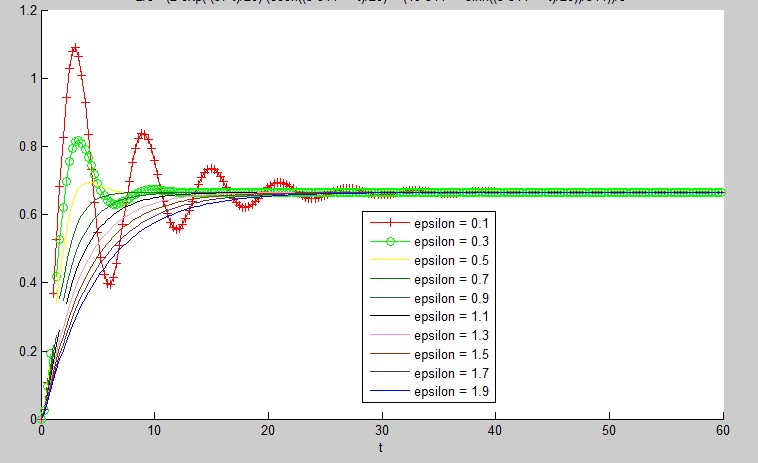
由于临界阻尼和无阻尼的情况在现实生活中比较难出现,二阶方程的根几乎不可能恰好,实部为0,或者两个实部相同且虚部为0. 于是,并为对以上两种较特殊的情况进行讨论。
选择欠阻尼和过阻尼两种情况进行分析讨论。
可以看出,当epsilon比较小的时候,响应时间短,且伴随有明显的超调。
随着epsilon的增大,超调明显降低,epsilon在0.7(恰巧工程上的最佳阻尼系数是0.7!)之后就没有超调了。随着epsilon的增大响应时间变得越来越长。
Wn = (1/T);
二阶方程的根
实部:X = -epsilon_0*Wn
虚部:Y = j*(Wn ).*sqrt(1-(epsilon_0).^2)
下图是上面十条曲线对应的根分布
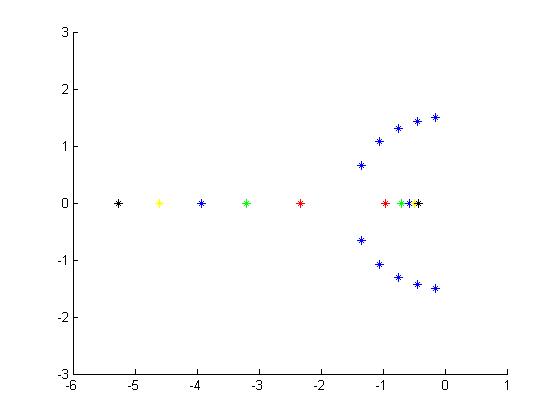
可以看出图中所有的点均位于Y轴左侧,说明最终响应都将收敛
虚部为0的点很好的对应了过阻尼状态(同样颜色的是一对实根),图中关于X轴对称的点,系统处于欠阻尼状态
下图是上升时间和阻尼系数epsilon之间的关系(欠阻尼状态下)
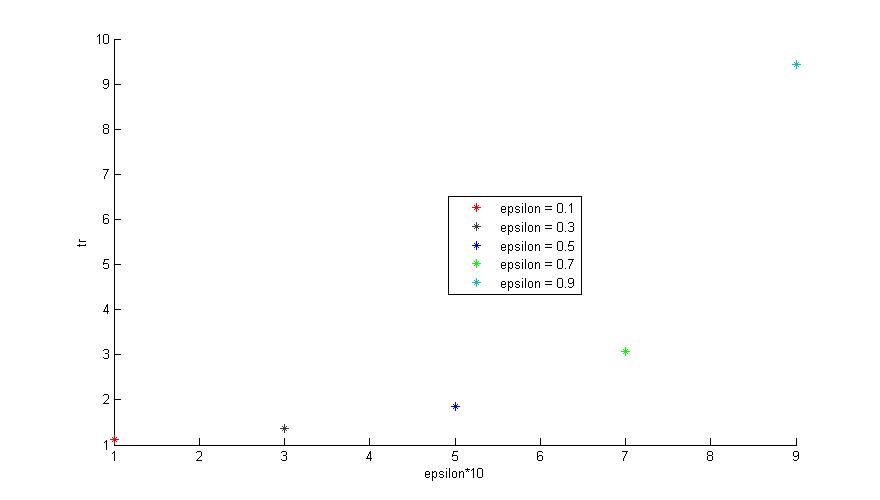
可以看出,随着阻尼系数的增大,上升时间变长!
matlab和本文相关代码:
%%*************************************************************
% code writer: EOF
% code date:2014.03.18
% e-mail: jasonleaster@gmail.com
% code purpose :
% I just want to share with someone who is interesting
% in adaptive control. This code is to help people to understand
% second order system.
%%**************************************************************
clear all
clc
syms s f t m;
K01 = 1;
K02 = 1;
K0 = (K01*K02)./(1+K01*K02);
hold on;
figure(1);
T0 = 1;
for epsilon_0 = 0.1:0.2:2T = T0./(1+K0);
% epsilon_0 = 0.5*(1/(K01*K02*T0));epsilon = epsilon_0./(1+K0);K = K0/(1+K0);f = (K./((T.^2).*(s.^2)+2*epsilon_0.*T.*s+K0)).*(1./s);m = ilaplace(f);ezplot(m,[0,120]);axis([0 60 0 1.2]);
end
legend('0.1','0.3','0.5','0.7','0.9','1.1','1.3','1.5','1.7','1.9');
hold off;
figure(2);
hold on;
for epsilon_0 = 0.1:0.2:2if epsilon_0 <1plot(-epsilon_0.*(1./T),(1./T).*sqrt(1-(epsilon_0).^2),'*');plot(-epsilon_0.*(1./T),-(1./T).*sqrt(1-(epsilon_0).^2),'*');elseif abs(epsilon_0-1.1) < 0.1 plot(-epsilon_0.*(1./T)+(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','r');plot(-epsilon_0.*(1./T)-(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','r');elseif abs(epsilon_0-1.3) < 0.1 plot(-epsilon_0.*(1./T)+(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','g');plot(-epsilon_0.*(1./T)-(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','g');elseif abs(epsilon_0-1.5) < 0.1 plot(-epsilon_0.*(1./T)+(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','b');plot(-epsilon_0.*(1./T)-(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','b');elseif abs(epsilon_0-1.7) < 0.1 plot(-epsilon_0.*(1./T)+(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','y');plot(-epsilon_0.*(1./T)-(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','y');elseif abs(epsilon_0-1.9) < 0.1 plot(-epsilon_0.*(1./T)+(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','k');plot(-epsilon_0.*(1./T)-(1./T).*sqrt((epsilon_0).^2-1),0,'*','Color','k');end
end
axis([-6 1 -3 3]);
hold off;
figure(3);
hold on;
Wn = (1./T);
for epsilon_0 = 0.1:0.2:2 Wd = Wn.*(1-(epsilon_0).^2);if epsilon_0 < 1belta = acos(epsilon_0);tr = (pi-belta)./Wd;plot(epsilon_0*10,tr,'*');end
end
legend('epsilon = 0.1','epsilon = 0.3','epsilon = 0.5','epsilon = 0.7','epsilon = 0.9');这篇关于second order system analysis 自动控制原理 二阶系统的matlab仿真分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






