nim专题

hdu 3032 Nim or not Nim? 博弈

题目大意： Alice和Bob轮流取N堆石子，每堆S[i]个，Alice先，每一次可以从任意一堆中拿走任意个石子，也可以将一堆石子分为两个小堆。先拿完者获胜。(1 ≤ N ≤ 10^6, 1 ≤ S[i] ≤ 2^31 - 1) 做到这道题目我想到了以前的一道题目和尼姆博弈尼姆博弈--------->>>>点击打开链接(以前的题目）可以看到S[i]的值可能非常大，如果计算每一堆

HDU 1730 Northcott Game NIM游戏

其实水题一道，你只需要把矩阵分成每一行一个游戏，每一行只要他们紧邻着那么黑色的必输，然后进行nim异或就行了。。但是我因为没加abs错了4遍。。。 Description Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？游戏规则是这样的：　　如图所示，游戏在一个n行

HDU 1849 Rabbit and Grass NIM游戏

Description 大学时光是浪漫的，女生是浪漫的，圣诞更是浪漫的，但是Rabbit和Grass这两个大学女生在今年的圣诞节却表现得一点都不浪漫：不去逛商场，不去逛公园，不去和AC男约会，两个人竟然猫在寝食下棋…… 说是下棋，其实只是一个简单的小游戏而已，游戏的规则是这样的： 1、棋盘包含1*n个方格，方格从左到右分别编号为0，1，2，…，n-1； 2、m个棋子放在棋盘

博弈论详解 1（基本理论定义和 Nim 游戏）

公平博弈游戏一般是两个玩家，轮流操作。是否能够必胜只和当前局面相关，不与现在是轮到哪个玩家相关（说白了就是不分黑白棋子，格点也不分黑白，都一样）。固定了开始状态后，可能的局面数是有限的。游戏一定会在有限步内结束怎么才能赢？必胜局面与必败局面我们定义当前的局面对于先手（指的是要对当前局面进行操作的人，下面对先手的定义也相同）是必胜的为 N N N 局面，必败为 P P P 局面。

博弈论（Nim 游戏）

公平组合游戏ICG 若—个游戏满足: 由两名玩家交替行动;在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关;不能行动的玩家判负; 则称该游戏为一个公平组合游戏。 NIM博弈属于公平组合游戏，但城建的棋类游戏，比如围棋，就不是公平组合游戏。因为围棋交战双方分别只能落黑子和白子，胜负判定也比较复杂，不满足条件 2 2 2 和条件 3 3 3。可以看出，公平组合游戏不存在平局，而且

poj2975 Nim

Nim博弈,问有多少种胜利的方法, 因为答案最多只有n，令ans=a1^a2^...^an,如果需要构造出异或值为0的数，而且由于只能操作一堆石子，所以对于某堆石子ai,现在对于ans^ai，就是除了ai以外其他的石子的异或值，如果ans^ai< ai，那么对于ai的话，是可以减小到ans^ai的值。将结果统计。 Source CodeProblem: 2975 User: 455

POJ 2975 Nim（尼姆博弈的变形）

题目大意有 n(1≤n≤1000) 堆石子，每堆石子数量为 1 到 1,000,000,000 之间的一个整数。两人玩游戏。每回合，游戏者必须从某堆中取走至少一个石子，取走最后一个石子的人获胜。问先手第一步有多少种走法使得他/她获胜解题思路 Nim 游戏的简单变形说明：下面的 '^' 符号表示 “异或” 的意思先求出所有的石子数量的 Nim 和，设为 sum。对于

POJ 2975 Nim题解

【题意】：给定一种Nim状态（相当于含N堆石头），求能有几种方法能通过调整某一堆石头的状态（只准取出），使新的Nim状态为必败态。（或者说求出所给的Nim游戏状态有多少种方法能够赢）【分析】： Nim游戏是什么，参见百度百科：百度百科_Nim 在证明Nim游戏的SG函数的“根据这个判断被判为N-position的局面一定可以移动到某个P-position”命题时，有这么一段证明：对于某

BNU17047-nim博弈

题目：题目链接题意：题目意思很明确。就是现在有N个数字，每次一个人上去，可以把一个数字换成它的一个因子替换。直到有一个人使得所有的数字的乘积为1的时候，这个人就赢了。分析：因为我们知道：对于任意一个数字A，我们都可以把这个数字写成A=p1^q1 * p2^q2 * ……* pn^qn (pi是质数)、所以我们每次的操作就相当于任选一个数字。然后从中拿走若干素数。这样的话

Nim游戏博弈

Nim游戏的概述：还记得这个游戏吗？给出n列珍珠，两人轮流取珍珠，每次在某一列中取至少1颗珍珠，但不能在两列中取。最后拿光珍珠的人输。后来，在一份资料上看到，这种游戏称为“拈（Nim）”。据说，它源自中国，经由被贩卖到美洲的奴工们外传。辛苦的工人们，在工作闲暇之余，用石头玩游戏以排遣寂寞。后来流传到高级人士，则用便士（Pennies），在酒吧柜台上玩。最有名的玩法，是把十二枚便士放成3、

Jack and Jim are playing an interesting stone game. At the beginning of the game there are N pile(s) of stones. Each pile has Pi (i = 1..N, 1 ≤ Pi ≤ 2 ∗ 10^9) stones. They take turns to take away some

Misere Nim （LightOJ - 1253，最后取石子输的 Nim 博弈）

一.题目链接： LightOJ-1253 二.题目大意：规则和 Nim 博弈相似，只不过规定最后一名取石子的人输. 三.分析：当所有石子堆均为 1 时，只需看 n 的奇偶性. 当 n 为奇数时，先手必输. 否则，后手必输. 在其余状态中，与 Nim 博弈一样因为只是两名玩家的选择策略产生了变化使自己拿最后一个 -> 使别人拿最后一个四.代码实现： #inclu

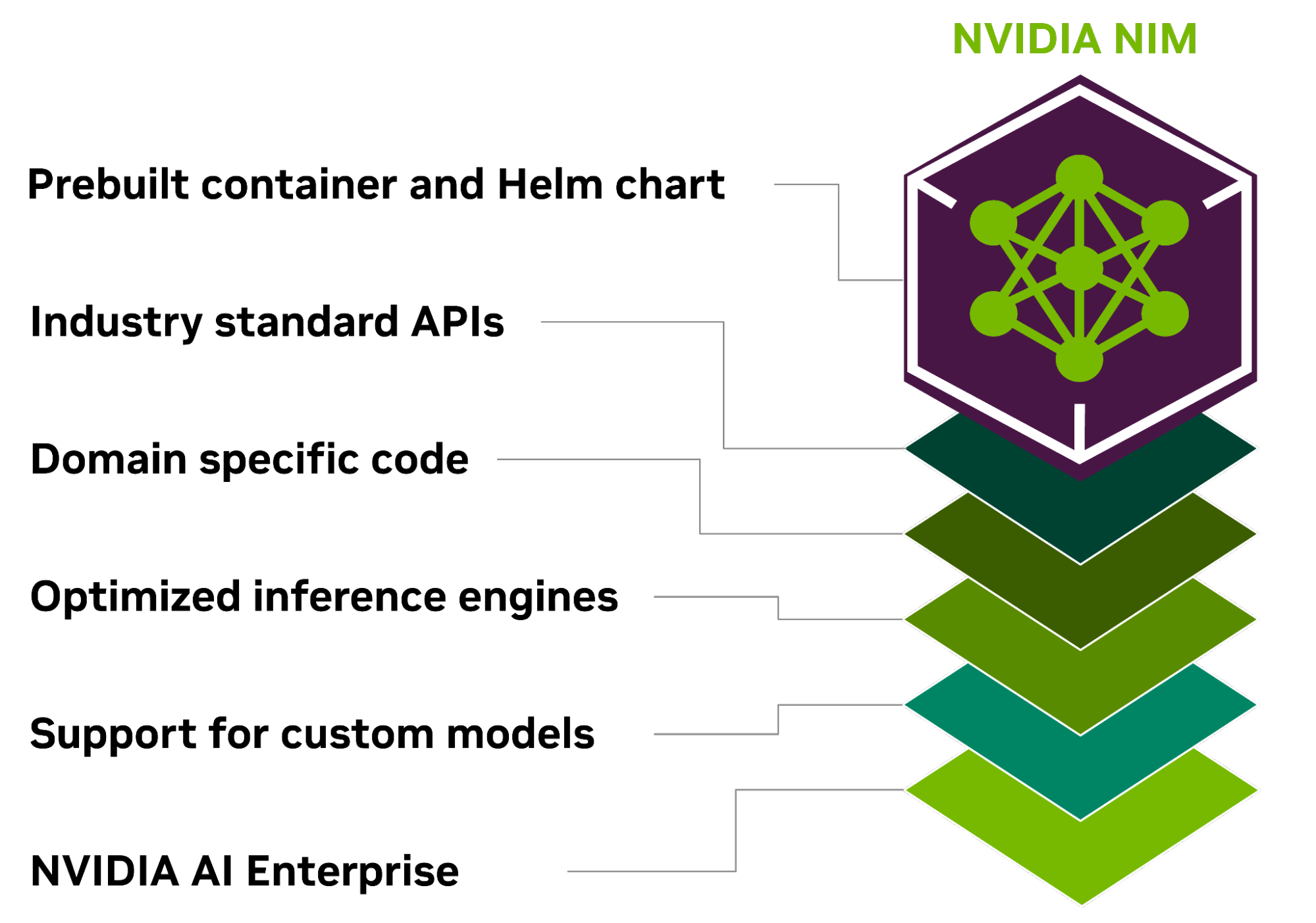
NVIDIA NIM 提供优化的推理微服务以大规模部署 AI 模型

NVIDIA NIM 提供优化的推理微服务以大规模部署 AI 模型生成式人工智能的采用率显着上升。在 2022 年 OpenAI ChatGPT 推出的推动下，这项新技术在几个月内就积累了超过 1 亿用户，并推动了几乎所有行业的开发活动激增。到 2023 年，开发人员开始使用来自 Meta、Mistral、Stability 等的 API 和开源社区模型进行 POC。进入 202

Nim游戏(转载)

Nim游戏(转载)Nim游戏是博弈论中最经典的模型（之一？），它又有着十分简单的规则和无比优美的结论Nim游戏是组合游戏(Combinatorial Games)的一种，准确来说，属于“Impartial Combinatorial Games”（以下简称ICG）。满足以下条件的游戏是ICG（可能不太严谨）：1、有两名选手；2、两名选手交替对游戏进行移动(move)，每次一步，选手可以在（一般而

编程之美 1.12 nim(2)

参考：http://tieba.baidu.com/p/613078798?pn=1 有若干堆石头，A，B分布依次取，一次只能选择一堆，从这堆中选择大于0的石头，问：1，如果最后取光石头的人获胜，A在什么情况下获胜？2，如果最后取光石头的人失败，A在什么情况下获胜？ 1. 在规则1下，先手获胜的情况，在规则2下先手同样获胜 2. 规则1和规则2的取法不一样。设当石头出现

1.11 nim

http://icyxiangzi.blog.163.com/blog/static/1697789052010102710296503/ 问题分析：没人每次可以拿一块，或相邻的两块。拿光者胜。必胜策略：若有奇数个，则取中间一个。以后跟着对手取，保持两边的对称性。若有偶数个，则取中间两个。扩展问题一：最后拿光者败。分析：设共有x个。 x=1，败。 x=2，胜。

#线性基，博弈论#洛谷 4301 JZOJ 3200 BZOJ 3105 新Nim游戏

题目 Nim游戏进阶，第一轮可以拿走若干堆的石子，之后与Nim游戏相同问先手是否必胜，是的话输出第一轮拿走的最小值，不是输出-1 分析那么 N i m Nim Nim游戏先手必胜当且仅当A1 xor A2 xor…xor An不等于0，那么就要让把等于0的情况去掉，那么可以用到线性基，当无法插入也就说明异或和为0，所以累计答案，但是题目又说取最小值，那么从大到小排序，让大的早点被取掉

POJ 2960 S-Nim

http://poj.org/problem?id=2960 这个题算是比较简单的博弈了，跟那个只能取fibonacci数博弈一样求没堆石子的sg值，然后看异或之后是否为0，为0是必败态，否则为必胜态 #include <iostream>#include <cstdio>#include <cstring>#include <algorithm>using namespac

LeetCode 0292.Nim 游戏：脑筋急转弯

【LetMeFly】292.Nim 游戏：脑筋急转弯力扣题目链接：https://leetcode.cn/problems/nim-game/ 你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合，你作为先手。每一回合，轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石

算法每日一题： Nim游戏 | 找规律

哈哈，大家好，我是星恒，今天的每日一题真开心，连做了3天牢，终于ak了一道，太不容易了这道题其实就是找规律，刚开始我还以为是动归，但是列举了不少例子之后，发现有自己直接的规律，ok，直接通过期待大家和我有一样的体验哈！让我们来看一看吧！题目：leetcode 292你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合， **你作为先手 **。每一回合

LeetCode--代码详解 292.Nim游戏

292.Nim游戏题目你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合，你作为先手。每一回合，轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢，返回 true；否则，返回 false 。示例 1：输入：n = 4

【LeetCode: 292. Nim 游戏+ 博弈问题】

leetcode 292. Nim 游戏【数学】

原题链接：292. Nim 游戏题目描述：你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合，你作为先手。每一回合，轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢，返回 true；否则，返回 false 。输入输出描

【Leetcode】292. Nim 游戏

文章目录题目思路代码结果题目题目链接你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合，你作为先手。每一回合，轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢，返回 true；否则，返回 false。

B组20-T2-博弈论-NIM游戏

NIM游戏： N堆物体，每堆A[i]个，二人轮流取，可取每堆里任意个（不可不取），取走最后一个的人赢，求先手状态。题解：取奇数堆 xor,得0则先手必输，反之必赢。附题：4178：游戏

每日一题力扣292 Nim游戏

292. Nim 游戏题目描述：你和你的朋友，两个人一起玩 Nim 游戏：桌子上有一堆石头。你们轮流进行自己的回合，你作为先手。每一回合，轮到的人拿掉 1 - 3 块石头。拿掉最后一块石头的人就是获胜者。假设你们每一步都是最优解。请编写一个函数，来判断你是否可以在给定石头数量为 n 的情况下赢得游戏。如果可以赢，返回 true；否则，返回 false 。示例 1：输入：