mean专题

mean shift图像分割（一）

mean shift均值偏移算法，可以用于图像分割（类聚）或者视频跟踪。在图像分割上是寻找一副图像的特征空间中的概率密度极值点，以极值点为类聚来平滑分隔。概率密度主要用非参数概率密度估计方法，其中核密度估计较为常用。密度极值点的寻找用密度梯度方法进行迭代寻找。 meanshift可分割需要建立在图像特征空间可分的基础上，也就是需要找到一个合适的特征空间，图像映射到这个空间上后，目标和背景可以

NumPy（五）：数组统计【平均值：mean()、最大值：max()、最小值：min()、标准差：std()、方差：var()、中位数：median()】【axis=0：按列运算；axis=0：按列】

统计运算 np.max()np.min()np.median()np.mean()np.std()np.var()np.argmax(axis=) — 最大元素对应的下标np.argmin(axis=) — 最小元素对应的下标 NumPy提供了一个N维数组类型ndarray，它描述了相同类型的“items”的集合。（NumPy provides an N-dimensional array

Pandas-高级处理（四）：分组与聚合【分组：groupby、聚合统计：max/min/mean...、分组转换：transform、一般化Groupby方法：apply】【抛开聚合只谈分组没意义】

df.groupby(by=None, axis=0, level=None, as_index=True, sort=True, group_keys=True, squeeze=False, **kwargs) 分组统计 - groupby功能 ① 根据某些条件将数据拆分成组 ② 对每个组独立应用函数 ③ 将结果合并到一个数据结构中应用groupby和聚合函数实现数据的分组与聚合

What does `return x ? : 1` mean in C language? [duplicate] stackoverflow

#include <stdio.h>int f(int x){return x?:1;}int main(){printf("f %d\n", f(0));printf("f %d\n", f(1));return 0;} And got the following output f 1f 1 And when I change it to int f(int x){r

torch.mean

mean()函数的参数：dim=0,按行求平均值，返回的形状是（1，列数）；dim=1,按列求平均值，返回的形状是（行数，1）,默认不设置dim的时候，返回的是所有元素的平均值。 x=torch.arange(12).view(4,3)'''注意：在这里使用的时候转一下类型，否则会报RuntimeError: Can only calculate the mean of floating t

sft是mean-seeking rl是mode-seeking

原文链接 KL散度是D(P||Q)，P和Q谁在前谁在后是有讲究的，P在前，就从P采样。 D K L ( P ∣ ∣ Q ) = E x − p ( x ) ( l o g ( P ( x ) / Q ( x ) ) ) D_{KL}(P||Q)=E_{x-p(x)}(log(P(x)/Q(x))) DKL(P∣∣Q)=Ex−p(x)(log(P(x)/Q(x)))想象一下，如果某个x的Q=

数学基础 -- 均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理

均方误差（Mean Squared Error, MSE）与交叉熵（Cross-Entropy）的数学原理 1. 均方误差（Mean Squared Error, MSE）均方误差主要用于回归问题，度量预测值与实际值之间的平均平方差。其数学公式为： MSE = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{n} \sum_{i

深度学习-k-mean实现聚类

对模拟函数生成的随机数据，分为三个族群。 1.生成数据设定样本数量、特征数、族群数，以及簇内标准差之后，通过make_blobs生成随机数据。 scikit-learn库中的make_blobs函数来生成模拟数据集的，用于创建多类单标签数据集，通常用于聚类算法的实验或测试。 make_blobs函数，将返回的两个值分别赋值给变量x和y。x通常是一个二维数组，其中包含了生成的样本点（每个样

【Python系列】探索 NumPy 中的 mean 函数：计算平均值的利器

💝💝💝欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。推荐:kwan 的首页,持续学习,不断总结,共同进步,活到老学到老导航檀越剑指大厂系列:全面总结 java 核心技术,jvm,并发编程 redis,kafka,Spring,微服务等常用开发工具系列:常用的开发工具,IDEA,M

Caffe学习：使用pycaffe生成mean_file.py文件

利用build/tools/compute_image_mean产生mean.binaryproto文件后，利用如下代码产生mean.npy文件，给pycaffe调用： #!/usr/bin/env pythonMEAN_BIN = 'mean.binaryproto'MEAN_NPY = 'mean.npy'from caffe.proto import caffe_pb2from caf

Caffe学习：build/tools/compute_image_mean

caffe/build/tools/compute_image_mean用于计算训练图片均值，在利用模型进行分类时需要用到编写命令，实现图片格式转化： #!bin/sh# 工具目录TOOLS_ROOT=caffe/build/tools# train_db是db文件夹目录，mean.binaryproto是生成的均值文件名$TOOLS_ROOT/compute_image_mean

【Pandas驯化-03】Pandas中常用统计函数mean、count、std、info使用

【Pandas驯化-03】Pandas中常用统计函数mean、count、std、info使用本次修炼方法请往下查看 🌈 欢迎莅临我的个人主页 👈这里是我工作、学习、实践 IT领域、真诚分享踩坑集合，智慧小天地！ 🎇 相关内容文档获取微信公众号 🎇 相关内容视频讲解 B站 🎓 博主简介：AI算法驯化师，混迹多个大厂搜索、推荐、广告、数据分析、数据挖掘岗位个人申请专利

npm WARN build `npm build` called with no arguments. Did you mean to `npm run-script build`

跑npm build结果如下： npm WARN build `npm build` called with no arguments. Did you mean to `npm run-script build` 把指令改成 npm run build 即可

【NumPy】关于numpy.mean()函数，看这一篇文章就够了

🧑 博主简介：阿里巴巴嵌入式技术专家，深耕嵌入式+人工智能领域，具备多年的嵌入式硬件产品研发管理经验。 📒 博客介绍：分享嵌入式开发领域的相关知识、经验、思考和感悟，欢迎关注。提供嵌入式方向的学习指导、简历面试辅导、技术架构设计优化、开发外包等服务，有需要可加文末联系方式联系。 💬 博主粉丝群介绍：① 群内高中生、本科生、研究生、博士生遍布，可互相学习，交流困惑。② 热榜t

deepstream std mean 对应的计算方法

pytorch中经典值mean=[0.485, 0.456, 0.406]，std = [0.229, 0.224, 0.225] 在deepstream中的计算方法 deepstream 对应计算公式：y = net scale factor*(x-mean) ，deepstream中mean也叫作offset deepstream中mean(offset)计算方法为： np.array(

【NumPy】之常见运算（min、max、mean、sum、exp、sqrt、sort、乘法、点积、对象拼接/切分）

____tz_zs 之前把 numpy 资料写在了同一篇博客里，发现非常难以查阅，于是按功能切分开来。 https://blog.csdn.net/tz_zs/article/details/73929778 https://blog.csdn.net/tz_zs/article/details/80773612 https://blog.csdn.net/tz_zs/article/det

13,12_基本运算,add/minus/multiply/divide,矩阵相乘mm,matmul,pow/sqrt/rsqrt,exp/log近似值,统计属性,mean,sum,min,max

1.12.基本运算 1.12.1.add/minus/multiply/divide 1.12.2.矩阵相乘mm,matmul 1.12.3.pow/sqrt/rsqrt 1.12.4.exp/log 1.12.5.近似值floor、ceil、trunc、frac、round 1.12.6.现幅max、min、median、clamp 1.13.统计属性 1.13.1.norm 1.13.2.me

8、InfluxDB常用函数(一)聚合函数，count()函数，DISTINCT()函数，MEAN()函数，MEDIAN()函数，SPREAD()函数，SUM()函数

8.InfluxDB学习之InfluxDB常用函数(一)聚合函数 8.1.count()函数 8.2.DISTINCT()函数 8.3.MEAN()函数 8.4.MEDIAN()函数 8.5.SPREAD()函数 8.6.SUM()函数 8.InfluxDB学习之InfluxDB常用函数(一)聚合函数 8.1.count()函数返回一个（field）字段中的非空值的数量。语法： SEL

[论文笔记]Root Mean Square Layer Normalization

引言今天带来论文Root Mean Square Layer Normalization的笔记，论文题目是均方根层归一化。本篇工作提出了RMSNorm，认为可以省略重新居中步骤。简介层归一化对Transformer等模型非常重要，它可以帮助稳定训练并提升模型收敛性，因为它能够处理输入和权重矩阵的重新居中(re-centering)和重新缩放(re-scaling)。然而，Layer

torch.mean()的使用方法

对一个三维数组的每一维度进行操作 1，dim=0 a = torch.Tensor([0, 1, 2, 3, 4, 5,6,7]).view(2, 2, 2) print(a) mean = torch.mean(a, 0) print(mean, mean.shape) 输出结果： tensor([[[0., 1.], [2., 3.]],

Google Earth Engine中的mean()与median()：何时使用哪一种？

引言：在使用Google Earth Engine（GEE）进行数据分析和影像处理时，我们经常会遇到需要对影像进行聚合的情况。而在GEE中，mean()和median()是两个常用的聚合函数。但是，什么时候使用mean()，什么时候使用median()呢？这篇文章将为您详细解答。 mean()与median()的定义：在GEE中，mean()函数通过计算所有匹配波段堆栈中每个像素的所

理解Mean-Variance Portfolio Theory In MPT

Markowitz Mean-Variance Portfolio Theory An investment instrument that can be bought and sold is often called an asset. Suppose we purchase an asset for x 0 x_0 x0 dollars on one date and then late

混合使用Objective-C，C++和Objective-C++ 以及错误Unknown type name ‘class‘； did you mean ‘Class‘?

有时我们需要在OC的程序中使用已有的C++类，这时，我们可以把OC类的.m文件后缀改为.mm，就可以在里面使用C++类了。但是二者直接混用会出现一些问题以致编译无法通过，这时可以简单的通过把target中的compile source as改为oc++就可以通过编译。这是一个简单的做法，但两个世界确实很不一样，如此这样的深度混合有时会变地很棘手。但是如果使用默认compile类型就在引入C++

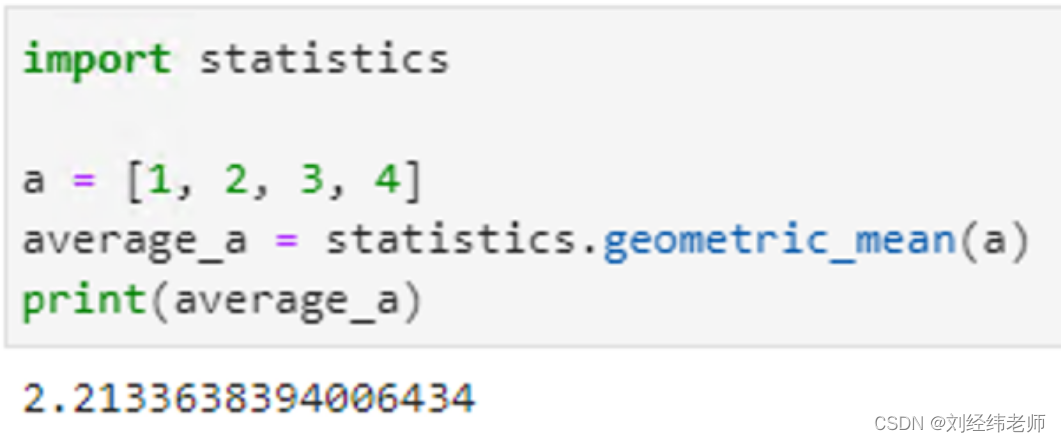
计算数据集的几何平均数geometric_mean

【小白从小学Python、C、Java】【计算机等考+500强证书+考研】【Python-数据分析】计算数据集的几何平均数 geometric_mean [太阳]选择题 geometric_mean的作用是？ import statistics a = [1, 2, 3, 4] average_a = statistics.geometric_mean(a) print(average_

Windows Socket 编程， WIN32_LEAN_AND_MEAN 的用法

一、基本Socket 调用原文地址：Getting Started with Winsock 注意关于windows.h 与 winsock2.h 一起使用时的问题： The Winsock2.h header file internally includes core elements from theWindows.h header file, so there is not usua

在pytorch模型中如何获得BatchNorm2d层的各个mean和var（平均值和方差）

这个内容是将随便做了一个网络结构，然后简单的训练几次，生成模型，并且存储起来，主要是为了学习获得pytorch中的BatchNorm2d层的各个特征图的平均值和方差。代码如下： import torchimport torch.nn as nnimport torch.nn.functional as Ffrom torchvision import datasets,transforms