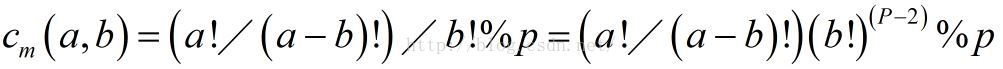lucas专题

CPC23三 K.（Lucas定理）

K.喵喵的神·数 Time Limit: 1 Sec Memory Limit: 128 MB Description 喵喵对组合数比较感兴趣，并且对计算组合数非常在行。同时为了追求有后宫的素质的生活，喵喵每天都要研究质数。我们先来复习一下什么叫做组合数。对于正整数P、T 然后我们再来复习一下什么叫质数。质数就是素数，如果说正整数N的约数只有1和它本身，N

OpenCV学习笔记（七）Lucas-…

原文地址：OpenCV学习笔记（七）Lucas-Kanade光流跟踪点的选择作者：ziguangzeng 在上一节提到了Lucas-Kanade光流跟踪算法，是一种准确，成熟，比较容易实现的物体跟踪算法，对画面中固定点会进行准确快速的跟踪。但是在视频中如何对移动物体进行跟踪以及跟踪点的选择，则是另一个需要解决的问题。下面我们来详细了解一下。首先，在视频中移动的物体与静止的物体

hdu5226 Tom and matrix 公式，Lucas

题意：给定x1,y1,x2,y2,求和C(i,j)，(x1<=i<=x2,y1<=j<=y2)，结果%p。分析：因为\sum_{i=a}^{b}C_{i}^{k}=C_{b+1}^{k+1}-C_{a}^{k+1}∑i=abCik=Cb+1k+1−Cak+1 所以求同一列的数的和可以变成求两个组合数的差。由于p可能很小，当除数为p的倍数时就为0了，直接乘逆元会出

【OpenCV】中使用 Lucas-Kanade 光流进行对象跟踪和路径映射

文章目录一、说明二、什么是Lucas-Kanade 方法三、Lucas-Kanade 原理四、代码实现4.1 第 1 步：用户在第一帧绘制一个矩形4.2 第 2 步：从图像中提取关键点4.3 第 3 步：跟踪每一帧的关键点一、说明本文针对基于光流法的目标追踪进行叙述，首先介绍Lucas-Kanade 方法的引进，以及基本推导，然后演示如何实现光流法的运动跟踪。并以Open

ZOJ 3557 How Many Sets II lucas 定理

插空法大组合数取余 #include <cstdio>#include <cstring>using namespace std;typedef long long LL;//求整数x和y，使得ax+by=d, 且|x|+|y|最小。其中d=gcd(a,b) void gcd(LL a, LL b, LL& d, LL& x, LL& y){if(!b){d = a;x = 1;

HDU 3037 Saving Beans 大组合数 lucas定理

直接lucas降到10w以内搞组合数 #include <cstdio>#include <cstring>typedef __int64 LL;LL f[110010];LL pow(LL a, LL b, LL c){LL ans = 1;while(b){if(b&1)ans = (ans*a) % c;b >>= 1;a = (a*a) % c;}return ans;}

HDU 5446 Unknown Treasure Lucas定理+中国剩余定理

数学本来就弱，现在大半年不练，果断简单题都不会了。。。先用lucas求出x mod 每一个素数结果，然后再用中国剩余定理解出x，不过要自己写乘法，防溢出。。。 #include <cstdio>#include <cstring>using namespace std;typedef __int64 LL;LL a[12], mm[12];LL mul(LL a, LL b, LL c

FZU 2020 组合 Lucas的应用

题意：给出组合数C(n,m), 表示从n个元素中选出m个元素的方案数。例如C(5,2) = 10, C(4,2) = 6.可是当n,m比较大的时候，C(n,m)很大！于是xiaobo希望你输出 C(n,m) mod p的值! Lucas的证明：点击打开链接 #include <iostream>#include <cstdio>#include <cstring>using namesp

计算机视觉——OpenCV实现Lucas-Kanade 光流

1.光流光流法是计算机视觉中用于估计图像序列中物体运动的关键技术。它类似于观察夜空中的彗星，通过其在天空中的运动轨迹来追踪它的路径。在图像处理中，光流帮助我们理解像素点如何在连续的帧之间移动。 1.1 稀疏光流法稀疏光流法关注于图像中的关键点（通常是角点或显著的特征点），并计算这些点在连续帧中的运动。Lucas-Kanade算法是这种方法的一个经典例子，它通过比较特征点在连续两帧中的灰度

Vision_MATH_Lucas定理及扩展

///定义： /* Lucas定理：（1）求解C(n,m)%p, n和m是非负整数，p是质数. （2）结论1. Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p); （3）结论2. 把n写成p进制a[n]a[n-1]a[n-2]...a[0]，把m写成p进制b[n]b[n-1]b[n-2].

Lucas模板（hdu-3037）

Lucas定理解决的问题是组合数取模。数学上来说，就是求：C(n，m)%p 这里n,m可能很大，比如达到10^15，而p在10^9以内。显然运用常规的阶乘方法无法直接求解，所以引入Lucas定理。如果素数P可以先确定，则可以O(P)预处理，每次计算时间复杂度为 O(logPlogN)。不预处理的时间复杂度，O(PlogN)。模板代码：（以hdu-3037为例） #pragma commen

OpenCV pyramid lk(Lucas Kanade)光流算法自己的一些注释

参考如下：代码注释的一个参考文章 https://blog.csdn.net/findgeneralgirl/article/details/107919541 原理参考文章 https://blog.csdn.net/qq_41368247/article/details/82562165 https://blog.csdn.net/sgfmby1994/article/details

c(n,m) mod p 1 Lucas 定理

普通的组合数C(n,m)在数据较小的情况下可以先用杨辉三角存储组合值，取模的话再%p即可。但是如果n,m很大，组合的结果自然很多，pascal自然不能完成任务，这样的取模问题可以使用数论里的Lucas定理来解决。数论Lucas定理是用来求 c(n,m) mod p的值,p是素数（从n取m组合，模上p）。描述为: Lucas(n,m,p)=Cm(n%p,m%p)* Lucas(n/p,m/p,p

BZOJ 1951 古代猪文（Lucas 中国剩余定理）

1951: [Sdoi2010]古代猪文 Time Limit: 1 Sec Memory Limit: 64 MB Description “在那山的那边海的那边有一群小肥猪。他们活泼又聪明，他们调皮又灵敏。他们自由自在生活在那绿色的大草坪，他们善良勇敢相互都关心……” ——选自猪王国民歌很久很久以前，在山的那边海的那边的某片风水宝地曾经存在过一个猪王国。猪王国地理位置偏僻，实施的是适应

【BZOJ 1951】 [Sdoi2010]古代猪文|数论|中国剩余定理|Lucas

搞清楚费马小定理的适用条件 #include <cmath>#include <cstdio>#include <iostream>#include <algorithm>using namespace std;#define LL long longconst int MO = 999911659;const int MO1= 999911658; int t[5]={0

BZOJ 2142 礼物拓展Lucas 解题报告

Description 一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物，当然他也会送出许多礼物。不同的人物在小E 心目中的重要性不同，在小E心中分量越重的人，收到的礼物会越多。小E从商店中购买了n件礼物，打算送给m个人，其中送给第i个人礼物数量为wi。请你帮忙计算出送礼物的方案数（两个方案被认为是不同的，当且仅当存在某个人在这两种方案中收到的礼物不同）。由于方案数可能会很

#数论，组合，容斥原理，lucas定理，乘法逆元#洛谷 CF451E Devu and Flowers

题目 n n n种颜色，每种颜色有 a i a_i ai枝花，现挑出 m m m朵，使没有颜色完全相同的方案分析可以发现，这道题是求多重集的组合数，根据容斥原理也就是 C k + r − 1 k − 1 − ∑ i = 1 k C k + r − n i − 2 k − 1 + ∑ 1 ≤ i < j ≤ k C k + r − n i − n j − 3 k − 1 −

[BZOJ 1951][Sdoi2010]古代猪文：Lucas定理|中国剩余定理|费马小定理|扩展欧几里得

点击这里查看原题一道综合了各种数论的神题。其实不难，主要是需要组合在一起运用。 1.费马小定理：求G^P时使用，因为G^(mod-1)%mod=1，所以需要P%=mod-1 2.Lucas定理&中国剩余定理：计算组合数取模时使用，但是本题中mod-1不为素数，因此需要结合中国剩余定理使用（即扩展Lucas定理） 3.扩展欧几里得：中国剩余定理要求逆元 /*User:SmallLan

[BZOJ 4403]序列统计：Lucas定理

点击这里查看原题统计长度在1到N之间，元素大小都在L到R之间的单调不降序列的数量。设M=R−L+1 长度为i，元素大小在1…M之间的单调不降序列的数量有C ( M−1 , i+M−1 ) 个，于是长度在1~N之间的数量有C ( M , N+M ) -1 个。点击这里查看公式推导 /*User:SmallLanguage:C++Problem No.:BZOJ 4403*/

「SDOI2010」古代猪文 - Lucas定理+CRT

题目描述 Luogu2480 题意简述：给定 n , G n,G n,G，求 G ∑ d ∣ n C n d mod 999911659 G^{\sum\limits_{d|n}C_n^d}\text{mod}\ 999911659 Gd∣n∑Cndmod 999911659 分析若 G mod 999911659 = 0 G\ \text{mod}\ 999911659=0

HDU3944 DP?(大组合数取模：lucas定理)

题意：有一个杨辉三角，现在从顶点到第n行第k列，只能向下或向右下，问最短路径和模p的值。要点：如果n>2*m，此时一直往斜左上走到边界，再一直向上，这样最短，权值总和为C（n+1,m）+（n-m)；如果n<=2*m，就先向上到边界，再斜左上到顶点，这样总和为C(n+1,m+1)+m。这里n和m很大，所以必须要用lucas定理，需要注意的是Lucas定理处理的p的范围大致为10^5数

基于光流法的车辆检测计数算法matlab仿真,对比Horn-Schunck光流和Lucas-Kanade光流

目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 Horn-Schunck光流法 4.2 Lucas-Kanade光流法 5.算法完整程序工程 1.算法运行效果图预览 HS光流 LK光流 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...................

bzoj4176 Lucas 的数论

======∑i=1n∑j=1nf(ij)∑i=1n∑j=1n∑d=1n2[dgcd(i,d)|j]∑i=1n∑d=1n2⌊n∗gcd(i,d)d⌋∑d=1n∑i=1⌊nd⌋∑j=1⌊n2d⌋⌊nj⌋e(gcd(i,j))∑d=1n∑i=1⌊nd⌋∑j=1n⌊nj⌋∑x|gcd(i,j)μ(x)∑x=1nμ(x)∑d=1n⌊ndx⌋∑j=1⌊nx⌋⌊njx⌋∑x=1nμ(x)(∑j=1⌊n

FZU 8月有奖月赛A Daxia Wzc's problem (Lucas)

Problem A Daxia & Wzc's problem Accept: 42 Submit: 228Time Limit: 1000 mSec Memory Limit : 32768 KB Problem Description Daxia在2016年5月期间去瑞士度蜜月,顺便拜访了Wzc,Wzc给他出了一个问题： Wzc给Daxia等差数列A(0),告诉

系数（牛客）lucas

实际就是求C(2*n,k)%3 代码： //#pragma GCC optimize("Ofast")//#pragma GCC target("avx,avx2,fma")//#pragma GCC optimization ("unroll-loops")#include <bits/stdc++.h>#define pb push_back#define ll long l