计算机视觉——OpenCV实现Lucas-Kanade 光流

2024-05-11 18:44
文章标签 实现 opencv 计算机 视觉 光流 lucas kanade

本文主要是介绍计算机视觉——OpenCV实现Lucas-Kanade 光流，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.光流

光流法是计算机视觉中用于估计图像序列中物体运动的关键技术。它类似于观察夜空中的彗星，通过其在天空中的运动轨迹来追踪它的路径。在图像处理中，光流帮助我们理解像素点如何在连续的帧之间移动。

1.1 稀疏光流法

稀疏光流法关注于图像中的关键点（通常是角点或显著的特征点），并计算这些点在连续帧中的运动。Lucas-Kanade算法是这种方法的一个经典例子，它通过比较特征点在连续两帧中的灰度值变化来估计这些点的运动。Lucas-Kanade方法适用于跟踪图像序列中的局部运动，尤其是当特征点清晰且显著时。

1.2 稠密光流法

与稀疏光流法不同，稠密光流法计算图像中每个像素的运动，生成一个速度场，其中每个像素都有一个对应的运动向量。Horn-Schunck算法是稠密光流法的一个代表，它通过平滑约束来优化光流场，假设图像亮度在物体运动的方向上变化不大。

1.3 Lucas-Kanade光流

在Lucas-Kanade光流中，图像的灰度值被视为位置和时间的函数。对于一个固定空间点，尽管其在世界坐标系中的位置是固定的，但在图像平面上的像素坐标会随着相机的运动会发生变化。Lucas-Kanade算法通过最小化重投影误差来估计这些像素坐标的变化，即：

I ( x , y , t ) = I ( x + Δ x , y + Δ y , t + Δ t ) I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t) I(x,y,t)=I(x+Δx,y+Δy,t+Δt)

其中， I ( x , y , t ) I(x, y, t) I(x,y,t)是在时间 t t t的图像中的灰度值， ( d x , d y ) (dx, dy) (dx,dy)是像素在图像平面上的位移，而 d t dt dt是时间间隔。通过建立一个关于位移 ( d x , d y ) (dx, dy) (dx,dy)的方程组，Lucas-Kanade算法可以估计出特征点的运动。

2. 光流基本假设推导过程

2.1. 光流法的基本假设：
光流法的基本假设是同一个空间点的像素灰度值，在各个图像中的是固定不变的。公式描述为：
I ( x , y , t ) = I ( x + Δ x , y + Δ y , t + Δ t ) I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t) I(x,y,t)=I(x+Δx,y+Δy,t+Δt)

2.2. 泰勒展开：
对上式右侧进行泰勒展开，得到：
I ( x + Δ x , y + Δ y , t + Δ t ) ≈ I ( x , y , t ) + ∂ I ∂ x Δ x + ∂ I ∂ y Δ y + ∂ I ∂ t Δ t I(x + \Delta x, y + \Delta y, t + \Delta t) \approx I(x, y, t) + \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t I(x+Δx,y+Δy,t+Δt)≈I(x,y,t)+∂x∂I​Δx+∂y∂I​Δy+∂t∂I​Δt

2.3. 光流约束方程：
因为假设了灰度不变，即 I ( x , y , t ) I(x, y, t) I(x,y,t)不随 Δ x , Δ y , Δ t \Delta x, \Delta y, \Delta t Δx,Δy,Δt变化，因此有：
∂ I ∂ x Δ x + ∂ I ∂ y Δ y + ∂ I ∂ t Δ t = 0 \frac{\partial I}{\partial x}\Delta x + \frac{\partial I}{\partial y}\Delta y + \frac{\partial I}{\partial t}\Delta t = 0 ∂x∂I​Δx+∂y∂I​Δy+∂t∂I​Δt=0

2.4. 速度和梯度：
将像素在 x 轴上的速度记为 u u u，在 y 轴上的速度记为 v v v，上述方程可以写为：
∂ I ∂ x u Δ t + ∂ I ∂ y v Δ t = − ∂ I ∂ t \frac{\partial I}{\partial x}u\Delta t + \frac{\partial I}{\partial y}v\Delta t = -\frac{\partial I}{\partial t} ∂x∂I​uΔt+∂y∂I​vΔt=−∂t∂I​

2.5. 矩阵形式：
写成矩阵形式有：
[ I x I y ] [ u v ] = − I t \begin{bmatrix} I_x & I_y \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = -I_t [Ix​​Iy​​][uv​]=−It​

2.6. 超定线性方程组：
在 Lucas-Kanade 光流中，引入了新的假设作为约束，即某一个窗口内的像素具有相同的运动。考虑一个大小为 w × h w \times h w×h 的窗口，其包含 k k k个像素。因为假设该窗口内像素具有相同的运动，因此可以得到 k k k个方程：
[ I x 1 I y 1 I x 2 I y 2 ⋮ ⋮ I x k I y k ] [ u v ] = − [ I t 1 I t 2 ⋮ I t k ] \begin{bmatrix} I_x^1 & I_y^1 \\ I_x^2 & I_y^2 \\ \vdots & \vdots \\ I_x^k & I_y^k \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} = -\begin{bmatrix} I_t^1 \\ I_t^2 \\ \vdots \\ I_t^k \end{bmatrix} ​Ix1​Ix2​⋮Ixk​​Iy1​Iy2​⋮Iyk​​ ​[uv​]=− ​It1​It2​⋮Itk​​ ​

记 A = [ I x 1 I y 1 ⋮ I x k I y k ] A = \begin{bmatrix} I_x^1 & I_y^1 \\ \vdots \\ I_x^k & I_y^k \end{bmatrix} A= ​Ix1​⋮Ixk​​Iy1​Iyk​​ ​ 和 b = [ I t 1 ⋮ I t k ] b = \begin{bmatrix} I_t^1 \\ \vdots \\ I_t^k \end{bmatrix} b= ​It1​⋮Itk​​ ​，则方程组可以写为：
A [ u v ] = b A\begin{bmatrix} u \\ v \end{bmatrix} = b A[uv​]=b

2.7. 最小二乘解：
该方程是关于 u u u 和 v v v 的超定线性方程组，可以使用最小二乘法求解：
[ u v ] ∗ = − ( A T A ) − 1 A T b \begin{bmatrix} u \\ v \end{bmatrix}^* = -(A^TA)^{-1}A^Tb [uv​]∗=−(ATA)−1ATb

值得注意的是，上述公式中的 I x , I y , I t I_x, I_y,I_t Ix​,Iy​,It​ 分别表示图像在该点的 x 方向梯度、y 方向梯度和时间方向的梯度。 Δ x , Δ y \Delta x,\Delta y Δx,Δy是像素点在图像平面上的位移，而 Δ t \Delta t Δt 是时间间隔。 u u u和 v v v是像素点在 x 和 y 方向上的速度。

3.OpenCV中calcOpticalFlowPyrLK函数

OpenCV中calcOpticalFlowPyrLK方法使用迭代Lucas-Kanade算法计算稀疏特征点的光流，用来做特征点跟踪，该方法使用了金字塔，因此具有一定的尺度不变性。
函数原型：

void cv::calcOpticalFlowPyrLK(	InputArray 	        prevImg,InputArray 	        nextImg,InputArray 	        prevPts,InputOutputArray 	nextPts,OutputArray 	    status,OutputArray 	    err,Size 	            winSize = Size(21, 21),int 	            maxLevel = 3,TermCriteria 	    criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01),int 	            flags = 0,double          	minEigThreshold = 1e-4 
);
  • prevImg:上一帧图像
  • nextImg:下一帧图像
  • prevPts:上一帧图像中关键点
  • nextPts:根据光流计算的上一帧关键点在当前帧中的位置
  • status:关键点的跟踪状态，vector,1表示OK,0表示LOST
  • err:每个特征点的跟踪误差vector<float>有len(status)==len(nextPts)==len(prePts)==len(err)
  • winSize:在每层金字塔中，LK算法中用来求解计算像素运动而假设具有相同运动的窗口大小。
  • maxLevel:金字塔的层数，层数多，尺度不变性能更好，运算时间更久
  • criteria:迭代搜索算法的终止条件,默认值表示在指定的最大迭代次数criteria.maxCount(30)之后或当搜索窗口移动小于criteria.epsilon(0.01)时终止迭代
  • flags:设置误差或者初始值参数,可选下面两个值：

    • OPTFLOW_USE_INITIAL_FLOW设置使用nextPts中的值作为迭代的初始值，如果不设置为OPTFLOW_USE_INITIAL_FLOW,初始状态就使用prevPts中的值，直接从prevPts复制到nextPts,OpenCV源码中对OPTFLOW_USE_INITIAL_FLOW的使用方式为:

      if( flags & OPTFLOW_USE_INITIAL_FLOW )nextPt = nextPts[ptidx]*(float)(1./(1 << level));
elsenextPt = prevPt;
      • OPTFLOW_LK_GET_MIN_EIGENVALS,flags设置为这个值时使用光流运动方程2x2的正规矩阵，也即空间梯度矩阵的最小特征值作为误差项。如果不设置成OPTFLOW_LK_GET_MIN_EIGENVALS,将原始点和移动点周围像素的距离除以窗口中的像素作为误差项。
  • minEigThreshold:迭代LK算法会计算光流运动方程2x2的正规矩阵，也即空间梯度矩阵的最小特征值，然后再除以运动不变窗口中的像素总数作为一个误差评价标准，当其小于minEigThreshold时，说明这个点已经追踪不到了，会将其从追踪特征点中移除，避免其对应相素运动的计算，可提升性能。

calcOpticalFlowPyrLK通常和goodFeatureToTrack方法一起使用，先使用GFTTDetector提取特征点的位置，再使用calcOpticalFlowPyrLK追踪其在连续视频流中的位置，避免了特征描述子的计算和特征点的匹配，可以极大的提升追踪的性能。

c++实现：

#include <memory> 
#include <vector>
#include <cstdlib>#include <opencv2/features2d.hpp>
#include <opencv2/opencv.hpp>// 定义一个名为TestOpticalFlowLK的类，用于处理光流跟踪
class TestOpticalFlowLK {public:// 使用std::shared_ptr来定义智能指针，便于管理类的实例typedef std::shared_ptr<TestOpticalFlowLK> Ptr;// 构造函数TestOpticalFlowLK();// 默认的析构函数// track函数用于处理特征点的跟踪void track(std::vector<cv::String> &filenames) const;private:// 使用cv::Ptr来定义一个智能指针，指向GFTTDetector对象cv::Ptr<cv::GFTTDetector> gftt_ptr_;
};// 实现TestOpticalFlowLK类的构造函数
TestOpticalFlowLK::TestOpticalFlowLK()
{// 初始化GFTTDetector对象，用于特征点检测gftt_ptr_ = cv::GFTTDetector::create(500, 0.2, 50);
}// 实现track函数，用于处理特征点的跟踪
void TestOpticalFlowLK::track(std::vector<cv::String> &filenames) const
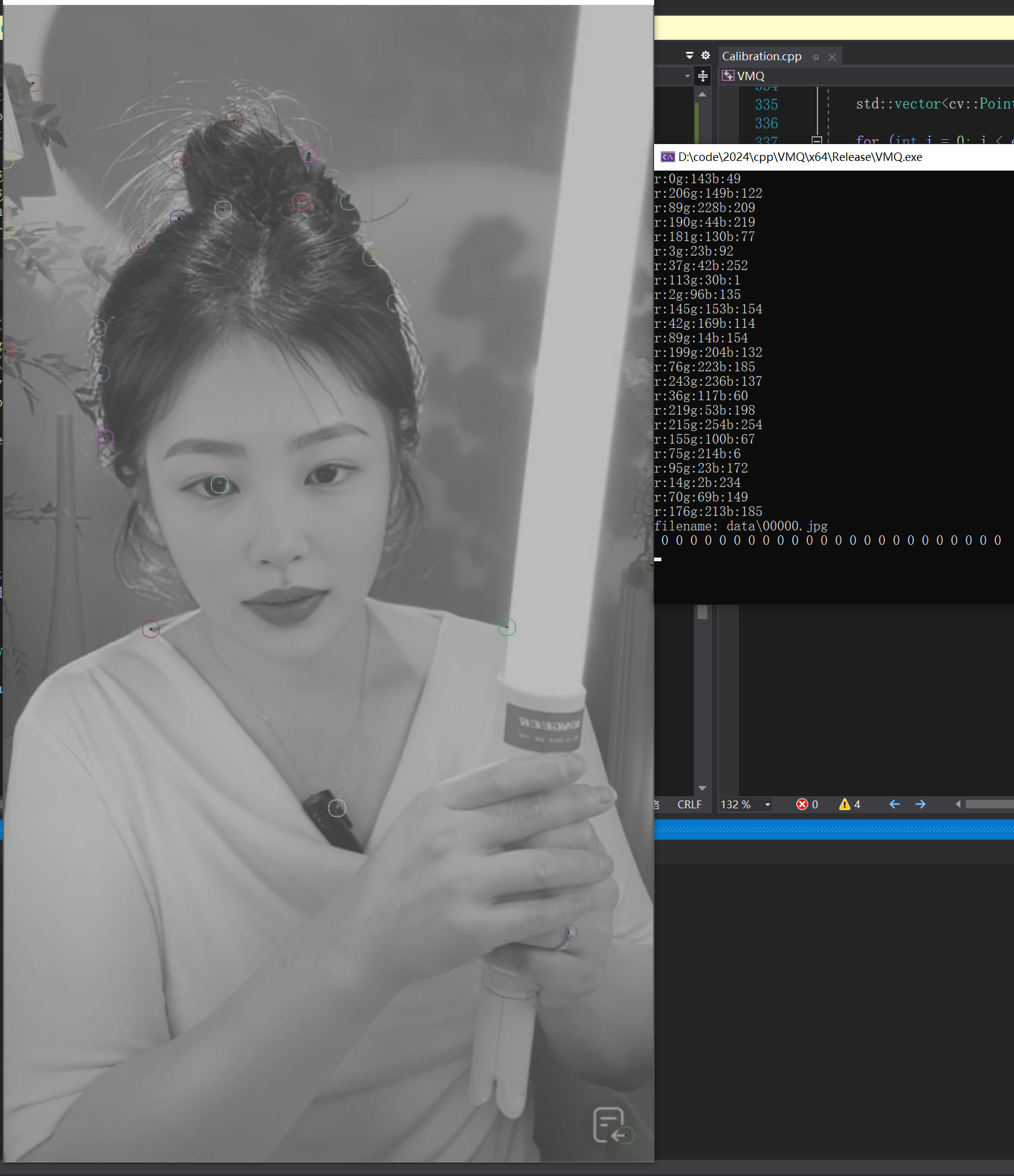
{// 确保filenames至少有一个元素assert(filenames.size() > 1);// 存储检测到的特征点std::vector<cv::KeyPoint> kps1;// 存储上一帧和当前帧中特征点的位置std::vector<cv::Point2f> pts1, pts2;// 存储绘制特征点时使用的颜色std::vector<cv::Scalar> colors;// 读取第一帧图像，并初始化last_imgcv::Mat last_img = cv::imread(filenames[0], 0), cur_img;// 创建一个掩码，用于绘制特征点cv::Mat mask(last_img.size(), CV_8UC1, 255);// 使用GFTTDetector检测第一帧图像中的特征点gftt_ptr_->detect(last_img, kps1, mask);// 遍历所有检测到的特征点for(auto &kp : kps1) {// 为每个特征点生成一个随机颜色int r = (int)(255. * rand() / (RAND_MAX + 1.f));int g = (int)(255. * rand() / (RAND_MAX + 1.f));int b = (int)(255. * rand() / (RAND_MAX + 1.f));// 输出随机颜色的值std::cout << "r:" << r << "g:" << g << "b:" << b << std::endl;// 将颜色添加到colors数组中colors.emplace_back(r, g, b);// 将特征点的位置添加到pts1和pts2数组中pts1.push_back(kp.pt);pts2.push_back(kp.pt);}// 存储特征点的跟踪状态std::vector<uchar> status;// 存储每个特征点的跟踪误差std::vector<float> err;// 将掩码转换为BGR格式，以便绘制cv::cvtColor(mask, mask, cv::COLOR_GRAY2BGR);// 创建一个Mat对象，用于存储绘制特征点后的图像cv::Mat frame;// 遍历所有提供的图像文件名for (auto &filename : filenames){// 输出当前处理的文件名std::cout << "filename: " << filename << std::endl;// 读取当前帧图像cur_img = cv::imread(filename, 0);// 使用calcOpticalFlowPyrLK计算特征点的光流cv::calcOpticalFlowPyrLK(last_img,cur_img,pts1,pts2,status,err,cv::Size(13, 13),3,cv::TermCriteria(cv::TermCriteria::COUNT + cv::TermCriteria::EPS, 30, 0.01),cv::OPTFLOW_USE_INITIAL_FLOW);// 将当前帧图像转换为BGR格式cv::cvtColor(cur_img, cur_img, cv::COLOR_GRAY2BGR);int cnt = 0; // 用于计数成功跟踪的特征点数量// 遍历所有特征点for(size_t i = 0; i < status.size(); i++) {// 输出当前特征点的跟踪误差std::cout << " " << err[i];// 如果特征点未成功跟踪，则跳过if(!status[i]) continue;// 如果特征点的移动距离超过80像素，则跳过if(abs((pts1[i].x - pts2[i].x)) > 80 || abs((pts1[i].y - pts2[i].y)) > 80) continue;// 在掩码上绘制特征点之间的连线cv::line(mask, pts1[i], pts2[i], colors[i], 2);// 在当前帧图像上绘制特征点cv::circle(cur_img, pts2[i], 10, colors[i], 1);// 更新pts1中的坐标为pts2中的坐标pts1[i].x = pts2[i].x;pts1[i].y = pts2[i].y;// 增加成功跟踪的特征点计数cnt += 1;}// 输出每帧成功跟踪的特征点数量std::cout << std::endl;// 将掩码和当前帧图像混合，以便同时显示原始图像和特征点cv::addWeighted(mask, 0.5, cur_img, 0.5, -65, frame);// 显示混合后的图像cv::imshow("frame", frame);// 等待用户按键，0表示无限等待cv::waitKey(0);// 更新last_img为当前帧图像cv::cvtColor(cur_img, cur_img, cv::COLOR_BGR2GRAY);last_img = cur_img;// 保存混合后的图像到文件cv::imwrite("frame.png", frame);}
}

在这里插入图片描述

Python 代码：

import cv2
import numpy as np
import randomclass TestOpticalFlowLK:def __init__(self):# 初始化GFTTDetector对象，用于特征点检测self.gftt_ptr_ = cv2.GFTTDetector_create(500, 0.2, 50)def track(self, filenames):assert len(filenames) > 1, "At least one filename is required"last_img = cv2.imread(filenames[0], 0)kps1 = self.gftt_ptr_.detect(last_img)pts1 = np.array([kp.pt for kp in kps1], dtype='float32')pts2 = np.zeros((len(pts1), 2), dtype='float32')colors = [((random.randint(0, 255), random.randint(0, 255), random.randint(0, 255)) for _ in range(len(kps1)))]status = np.zeros((len(pts1),), dtype='uint8')err = np.zeros((len(pts1),), dtype='float32')for filename in filenames[1:]:print("Processing file:", filename)cur_img = cv2.imread(filename, 0)pts2, status, err = cv2.calcOpticalFlowPyrLK(last_img, cur_img, pts1, pts2, None, winSize=(13, 13), maxLevel=3,criteria=(cv2.TERM_CRITERIA_COUNT | cv2.TERM_CRITERIA_EPS, 30, 0.01),flags=cv2.OPTFLOW_USE_INITIAL_FLOW)img = cv2.cvtColor(cur_img, cv2.COLOR_GRAY2BGR)for i, (pt1, pt2, stat) in enumerate(zip(pts1, pts2, status)):if stat:# 确保坐标是一维数组pt1 = pt1.reshape(-1)pt2 = pt2.reshape(-1)cv2.line(img, (int(pt1[0]), int(pt1[1])), (int(pt2[0]), int(pt2[1])), (255), 2)cv2.circle(img, (int(pt2[0]), int(pt2[1])), 10, (127), 1)pts1 = pts2.copy()last_img = cur_imgcv2.imshow("frame", img)cv2.waitKey(0)cv2.destroyAllWindows()if __name__ == "__main__":# 假设我们有一个包含图像文件路径的列表filenames = ['data/00001.jpg', 'data/00001.jpg', 'data/00002.jpg','data/00003.jpg']  # 以此类推flow_tracker = TestOpticalFlowLK()flow_tracker.track(filenames)

这篇关于计算机视觉——OpenCV实现Lucas-Kanade 光流的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/980346。

相关文章

python使用watchdog实现文件资源监控

python使用watchdog实现文件资源监控

《python使用watchdog实现文件资源监控》watchdog支持跨平台文件资源监控,可以检测指定文件夹下文件及文件夹变动,下面我们来看看Python如何使用watchdog实现文件资源监控吧... python文件监控库watchdogs简介随着Python在各种应用领域中的广泛使用，其生态环境也
阅读更多...
el-select下拉选择缓存的实现

el-select下拉选择缓存的实现

《el-select下拉选择缓存的实现》本文主要介绍了在使用el-select实现下拉选择缓存时遇到的问题及解决方案,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的... 目录项目场景：问题描述解决方案：项目场景：从左侧列表中选取字段填入右侧下拉多选框，用户可以对右侧
阅读更多...
Python pyinstaller实现图形化打包工具

Python pyinstaller实现图形化打包工具

《Pythonpyinstaller实现图形化打包工具》：本文主要介绍一个使用PythonPYQT5制作的关于pyinstaller打包工具,代替传统的cmd黑窗口模式打包页面,实现更快捷方便的... 目录1.简介2.运行效果3.相关源码1.简介一个使用python PYQT5制作的关于pyinstall
阅读更多...
使用Python实现大文件切片上传及断点续传的方法

使用Python实现大文件切片上传及断点续传的方法

《使用Python实现大文件切片上传及断点续传的方法》本文介绍了使用Python实现大文件切片上传及断点续传的方法,包括功能模块划分（获取上传文件接口状态、临时文件夹状态信息、切片上传、切片合并）、整... 目录概要整体架构流程技术细节获取上传文件状态接口获取临时文件夹状态信息接口切片上传功能文件合并功能小
阅读更多...
python实现自动登录12306自动抢票功能

python实现自动登录12306自动抢票功能

《python实现自动登录12306自动抢票功能》随着互联网技术的发展,越来越多的人选择通过网络平台购票,特别是在中国,12306作为官方火车票预订平台,承担了巨大的访问量,对于热门线路或者节假日出行... 目录一、遇到的问题？二、改进三、进阶–展望总结一、遇到的问题？1.url-正确的表头：就是首先ur
阅读更多...
C#实现文件读写到SQLite数据库

C#实现文件读写到SQLite数据库

《C#实现文件读写到SQLite数据库》这篇文章主要为大家详细介绍了使用C#将文件读写到SQLite数据库的几种方法,文中的示例代码讲解详细,感兴趣的小伙伴可以参考一下... 目录1. 使用 BLOB 存储文件2. 存储文件路径3. 分块存储文件《文件读写到SQLite数据库China编程的方法》博客中，介绍了文
阅读更多...
Redis主从复制实现原理分析

Redis主从复制实现原理分析

《Redis主从复制实现原理分析》Redis主从复制通过Sync和CommandPropagate阶段实现数据同步,2.8版本后引入Psync指令,根据复制偏移量进行全量或部分同步,优化了数据传输效率... 目录Redis主DodMIK从复制实现原理实现原理Psync: 2.8版本后总结Redis主从复制实
阅读更多...
JAVA利用顺序表实现“杨辉三角”的思路及代码示例

JAVA利用顺序表实现“杨辉三角”的思路及代码示例

《JAVA利用顺序表实现“杨辉三角”的思路及代码示例》杨辉三角形是中国古代数学的杰出研究成果之一,是我国北宋数学家贾宪于1050年首先发现并使用的,：本文主要介绍JAVA利用顺序表实现杨辉三角的思... 目录一：“杨辉三角”题目链接二：题解代码：三：题解思路：总结一：“杨辉三角”题目链接题目链接：点击这里
阅读更多...
基于Python实现PDF动画翻页效果的阅读器

基于Python实现PDF动画翻页效果的阅读器

《基于Python实现PDF动画翻页效果的阅读器》在这篇博客中,我们将深入分析一个基于wxPython实现的PDF阅读器程序,该程序支持加载PDF文件并显示页面内容,同时支持页面切换动画效果,文中有详... 目录全部代码代码结构初始化 UI 界面加载 PDF 文件显示 PDF 页面页面切换动画运行效果总结主
阅读更多...
SpringBoot实现基于URL和IP的访问频率限制

SpringBoot实现基于URL和IP的访问频率限制

《SpringBoot实现基于URL和IP的访问频率限制》在现代Web应用中,接口被恶意刷新或暴力请求是一种常见的攻击手段,为了保护系统资源,需要对接口的访问频率进行限制,下面我们就来看看如何使用... 目录1. 引言2. 项目依赖3. 配置 Redis4. 创建拦截器5. 注册拦截器6. 创建控制器8.
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2