lu专题
33、matlab矩阵分解汇总:LU矩阵分解、Cholesky分解和QR分解
1、LU矩阵分解 语法 语法1:[L,U] = lu(A) 将满矩阵或稀疏矩阵 A 分解为一个上三角矩阵 U 和一个经过置换的下三角矩阵 L,使得 A = L*U。 语法2:[L,U,P] = lu(A) 还返回一个置换矩阵 P,并满足 A = P'*L*U。 语法3:[L,U,P] = lu(A,outputForm) 以 outputForm 指定的格式返回 P。 1)矩阵的 LU 分解
lu用户体验_关闭按钮
【项目背景】 网盟用户体验太差,需要改进。从机制策略上,将用户体验作为广告主ROI、流量主收益外的第三种考量因素,纳入投放管理。 本功能主要两个作用:1-终端上保护用户体验,对最后露出的劣质创意/敏感词捞回;2-收集用户反馈,数据应用到机制,如创意控制、推词控制、样式改善等 【测试过程】 以下是新的测试结果,前期反馈的问题:(1)原生图片排行榜:个别尺寸浏览器展示不一致;(2)刷出公益广
lu值班:拉rb分流
在jenkins中查找lu-as,搜到最新的build,如图: 并在群里进行公布,并且附件上此次功能对应的卡片: 单击see more -> 最新的分支 -> 点击promotion status -> approve :这是build过程。 需要十几分钟左右会build成功。 接着是系统级测试:群里发消息,构建成功,求conf merge。 ->点击生成的build->pr
解线性方程组——直接解法:LU分解、PLU分解(类似列主元消去法) | 北太天元
L: lower triangular 下三角 U: upper triangular 上三角 LU 分解,顾名思义,为 把一个 矩阵 分成 一个下三角矩阵 乘上一个上三角矩阵的形式。 Example 为什么可以这样 几个基本的初等行变换,可以自己验算一下,等式的左边与右边是相等的 用上面这几个等式,重新看一下 第一个例子, 对A进行了三次行变换,得到上三角矩阵U, 两边同时左乘初等
【矩阵论】13——矩阵分解——LU/LDV分解
本系列文章由Titus_1996 原创,转载请注明出处。 文章链接:https://blog.csdn.net/Titus_1996/article/details/84377831 本系列文章使用的教材为《矩阵论》(第二版),杨明,刘先忠编,华中科技大学出版社。 LD分解 所谓LD分解就是方阵A与单位阵组成的增广矩阵进行行变换(相当于左乘一个矩阵P),那么P就变成了下三角,PA就
矩阵计算-线性系统和 LU 分解
一、三角系统 …… 二、高斯消元法 …… 三、LU分解--直接三角分解法 求解线性方程Ax=b: 参考视频:【数值分析】矩阵LU三角分解| 速成讲解 考试宝典_哔哩哔哩_bilibili 令A=L·U,其中L是单位下三角矩阵(对角线上元素都是1),U是上三角矩阵。 无论矩阵A是多少,都有唯一的单位下三角矩阵L和上三角矩阵U,使得A可以分解为L·U。 由矩阵乘法可
要想富,先有LU,超能鹿战队LU开盘涨幅240%
最近数字货币市场疲态初现,比特币迟迟突破不了1万美金。然而在餐饮这样一个细分领域,却出现了一道亮丽的风景线。 6月17日,LU正式登录EAT.FAN,上线累计涨幅257%。支撑起LU价格上涨的,是其背后千亿规模的瘦身饮食市场、庞大的社区用户群以及“区块链+瘦身饮食”的创新玩法。 “要想富,先有LU”。鹿粉社区通过LU经济模型设计,打造了一个完整的商业闭环。让用户通过“吃”这一轻松的方式获取收益
杜利特尔分解(LU分解)的JAVA代码
杜利特尔分解(LU分解)的JAVA代码 数学基础:设A为n阶方阵,满足其各阶主子式: det (Subscript[A, p]) != 0 A=LU 其代码如下: public static double[][] LUDecomposition(double a[][],String X)//X代表返回矩阵的种类,若为U,返回u矩阵;若为l,返回l矩阵。若为其他,返回a; {i
ASUS华硕ROG幻15冰刃4新锐_GX502LWS_GU502LWS,LXS,LW,LU,LI,LV工厂模式原厂Win10系统包下载 带Recovery恢复
华硕幻15笔记本冰刃4电脑原装出厂Windows10系统工厂包,恢复出厂开箱状态oem预装系统 适用型号:GU502LU、GU502LI、GU502LV、GU502LW、GU502LWS 链接:https://pan.baidu.com/s/1Egg7bm7Um_D1qrzvRtGoCA?pwd=o8m4 提取码:o8m4 带有ASUS RECOVERY恢复功能、自带所有驱动、系统属性专
线性代数笔记10——矩阵的LU分解
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。LU分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。 什么是LU分解 如果有一个矩阵A,将A表示成下三角矩阵L和上三角矩阵U的乘积,称为A的LU分解。 更进一步,我们希望下三角矩阵的对角元素
大名鼎鼎的LU分解——Matlab解线性方程组(3)
目录 前言 一、伟大的LU分解法 1.前向消去的步骤 2.LU分解有啥用? 二、多出的一步 1.为什么要选主元? 2.为什么会这样捏? 总结 前言 前文已经完成了铺垫,这里我们开始进行矩阵的LU分解。第一节我们看到了,因为求逆矩阵会导致运算时间增长、运算量增大,所以在一般求解线性方程组时,常用高斯消元的方法。将高斯消元法凝练、规范化,给出矩阵的LU分解法
CTF-PWN-堆-【chunk extend/overlapping-2】(hack.lu ctf 2015 bookstore)
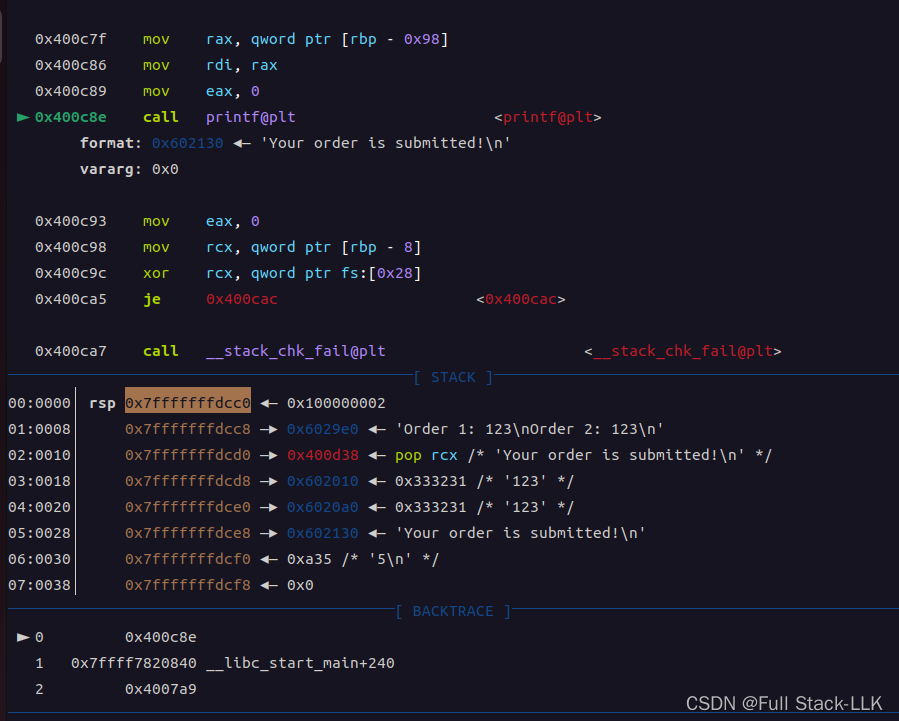
文章目录 hack.lu ctf 2015 bookstore检查IDA源码main函数edit_notedelete_notesubmit .fini_array段劫持(回到main函数的方法)思路python格式化字符串简化思路: exp 佛系getshell 常规getshell hack.lu ctf 2015 bookstore 检查 got表可写,没有地
线性代数 --- 为什么LU分解中L矩阵的行列式一定等于正负1?
以下是关于下三角矩阵L的行列式一定等于+-1的一些说明 笔者的一些话(写在最前面): 这是一篇小文,是我写的关于求解矩阵行列式的一篇文章中的一部分。之所以把这一段专门提溜出来,是因为这一段相对于原文是可以完全独立的,也是因为我自认为这是原文中很精彩的一段论证。为了便于我自己后续翻阅和查找,也是为了给我CSDN文章里面凑数,这才有了这篇文章。 证明:
线性代数 --- 为什么LU分解中的下三角矩阵L的主对角线上都是1?
为什么LU分解中的下三角矩阵L的主对角线上都是1? 一方面,对于LU分解而言,下三角阵L是对高斯消元过程的记录,是高斯消元的逆过程,是多个消元矩阵E的逆矩阵的乘积(形如下图中的下三角矩阵),即: 另一方面,根据矩阵的乘法原则两个矩阵A和B的乘积C中的元素,来自于矩阵A中第i行元素与矩阵B中第j列元素的乘积。 例如,在本例中矩阵C中的
【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解) A x = b , A = L U Ax=b \,\,,\,\, A=LU Ax=b,A=LU { L y = b U x = y \begin{cases} Ly=b \\ Ux=y \end{cases} {Ly=bUx=y 矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A
线性代数-Python-05:矩阵的逆+LU分解
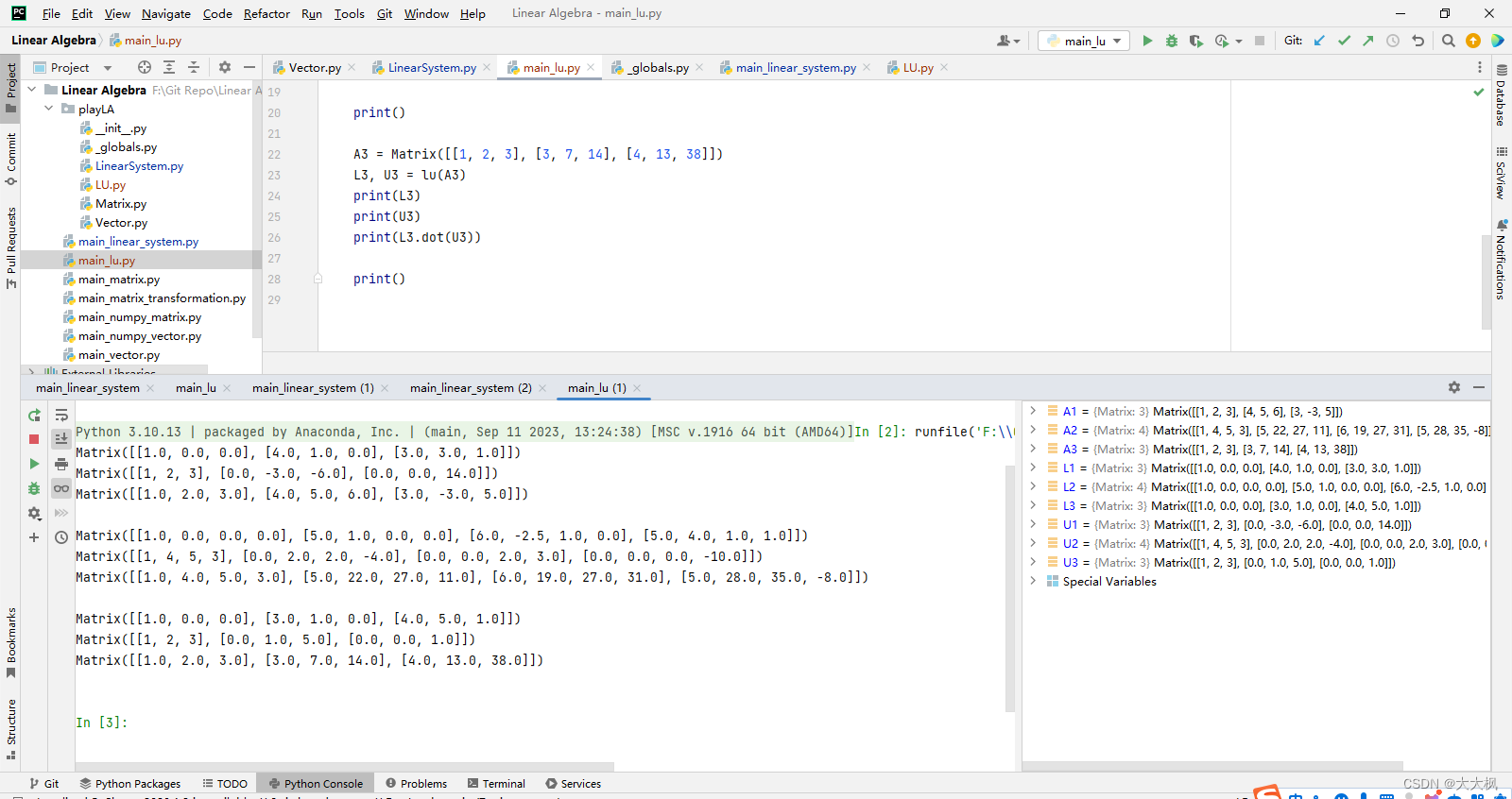
文章目录 1 矩阵的逆1.1 求解矩阵的逆 2 初等矩阵2.1 初等矩阵和可逆性 3 矩阵的LU分解3.1 LU分解的实现 1 矩阵的逆 1.1 求解矩阵的逆 def inv(A):if A.row_num() != A.col_num():return Nonen = A.row_num()"""矩阵A+单位矩阵"""ls = LinearSystem(A, Matr
线性代数-Python-05:矩阵的逆+LU分解
文章目录 1 矩阵的逆1.1 求解矩阵的逆 2 初等矩阵2.1 初等矩阵和可逆性 3 矩阵的LU分解3.1 LU分解的实现 1 矩阵的逆 1.1 求解矩阵的逆 def inv(A):if A.row_num() != A.col_num():return Nonen = A.row_num()"""矩阵A+单位矩阵"""ls = LinearSystem(A, Matr
uncle-lu的种草日记 赛氪
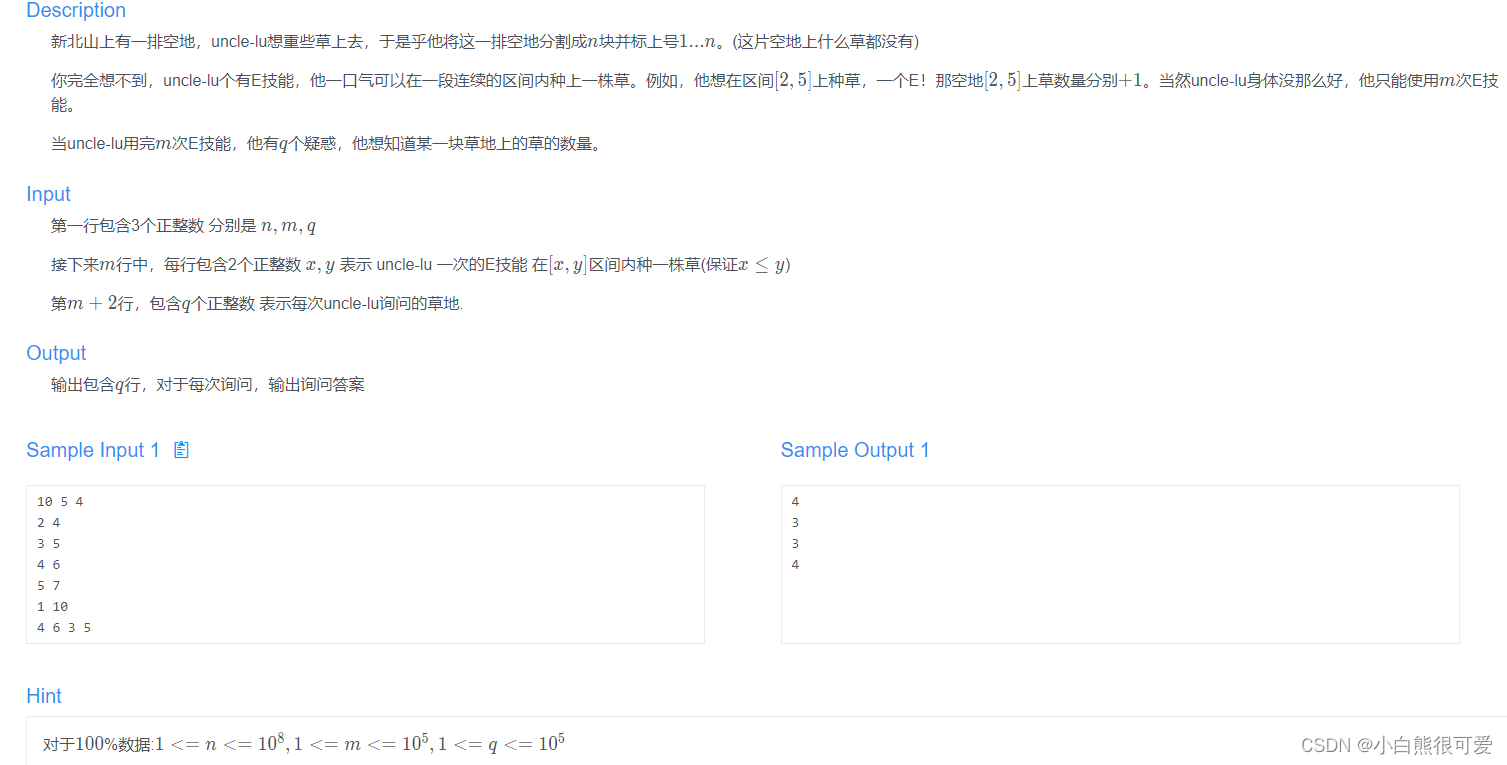
1.5.7 uncle-lu的种草日记 Description 新北山上有一排空地,uncle-lu想重些草上去,于是乎他将这一排空地分割成nn块并标上号1...n1...n。(这片空地上什么草都没有) 你完全想不到,uncle-lu个有E技能,他一口气可以在一段连续的区间内种上一株草。例如,他想在区间[2,5][2,5]上种草,一个E!那空地[2,5][2,5]上草数量分别+
04 MIT线性代数-矩阵的LU分解 Factorization into A=LU
目的: 从矩阵的角度理解高斯消元法, 完成LU分解得到A=LU 1.矩阵乘积的逆矩阵 Inverse of a product 2.矩阵乘积的转置 Transpose of a product 3.转置矩阵的逆矩阵 Inverse of a transpose 4.矩阵的LU分解 U为上三角阵(Upper triangular matrix), L为下三角阵(Lo
矩陣分析-線性系統-3 LU分解
http://www.cnblogs.com/pegasus/archive/2011/11/21/2257258.html 1. LU分解 LU分解在本質上是高斯消元法的一種表達形式。實質上是將A通過初等行變換變成一個上三角矩陣,其變換矩陣就是一個單位下三角矩陣。這正是所謂的杜爾裡特算法(Doolittle algorithm):從下至上地對矩陣A做初等行變換,將對角線左下方的元素
数值分析实验报告 Lab5 LU分解算法
数值分析实验报告 Lab5 LU分解算法 #include<stdio.h>#include<iostream>#include<math.h>#define MAX_SIZE 100 /* 矩阵最大维数 */#define ZERO 0.000000001 /* 当一个正数小于ZERO就认为该数是0 */using namespace std;/*LU方法计算 Ax=b*/bool