【矩阵论】13——矩阵分解——LU/LDV分解

本文主要是介绍【矩阵论】13——矩阵分解——LU/LDV分解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本系列文章由Titus_1996 原创，转载请注明出处。  

文章链接：https://blog.csdn.net/Titus_1996/article/details/84377831

本系列文章使用的教材为《矩阵论》（第二版），杨明，刘先忠编，华中科技大学出版社。

---

LD分解

所谓LD分解就是方阵A与单位阵组成的增广矩阵进行行变换（相当于左乘一个矩阵P）,那么P就变成了下三角，PA就变成了上三角。具体过程如下：

这就是线代中的我们求逆矩阵用过的方式，只不过求逆的时候变成的形式为

如此我们可以得到：

，令=，=。所以

---

LDV分解

LDV分解就是在LU分解的基础上，将U的对角线上全部化为1，这个D就是U的对角线上的元素组成的对角阵。

---

用LDV分解求解方程组.

设有方程组AX=b.

则上式可写为

                            

记得

又记得

 

所以我们把求解AX=b转化为了求

1. ,这里求出了，是下三角矩阵，很容易求。得出的带入下式继续求

2. ，这里求出了，是对角阵，也是很容易求得，得出的带入下式求

3. ，最后被求出来了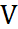，是上三角矩阵，很容易求出。

这篇关于【矩阵论】13——矩阵分解——LU/LDV分解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---