04 MIT线性代数-矩阵的LU分解 Factorization into A=LU

本文主要是介绍04 MIT线性代数-矩阵的LU分解 Factorization into A=LU，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目的: 从矩阵的角度理解高斯消元法, 完成LU分解得到A=LU

1.矩阵乘积的逆矩阵 Inverse of a product

2.矩阵乘积的转置 Transpose of a product

3.转置矩阵的逆矩阵 Inverse of a transpose

4.矩阵的LU分解

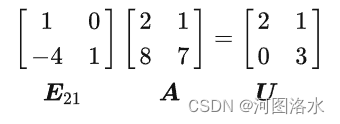
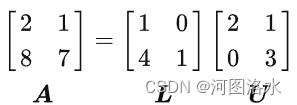
U为上三角阵(Upper triangular matrix), L为下三角阵(Lower triangular matrix), 通过分解得到对角阵D（diagonal matrix）

4.1 三阶矩阵不需要换行进行消元的情况则有: (no row exchanges)

设定一组消元矩阵，其中E31为单位阵I，其它两个消元矩阵如下:

row3-5newrow2=row3-5(row2-2row1)=row3-5row2+10 row1

E(left of A) EA=U

4.2 inverses (reverse order)

右侧操作则不会有这种情况发生，运算顺序会发生变化

E(left of U) A=LU

if no row exchanges, multipliers go directly into L  没有多余的交叉项出现是LU分解要优于EA=U这种形式的原因之一

5. How many operations on n×n matrix A? 消元法所需运算量

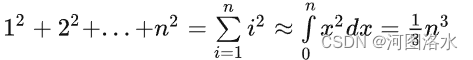
6. 置换矩阵Permutation Matrix

如果主元的位置出现了0，就需要进行“行交换”。我们可以通过左乘一个置换矩阵（Permutation Matrix）实现“行交换”的操作. 置换矩阵每一行或者每一列只有一个元素是1，其它都是0

为了实现33矩阵的第一行与第二行的交换, 有6个置换矩阵

nxn矩阵存在着n!个置换矩阵

置换矩阵的逆矩阵

某阶的置换矩阵集合而言，置换矩阵的两两乘积仍在这个集合中，置换矩阵的逆矩阵也在此集合中。置换矩阵的逆矩阵即为它的转置 

这篇关于04 MIT线性代数-矩阵的LU分解 Factorization into A=LU的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---