本文主要是介绍矩陣分析-線性系統-3 LU分解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. LU分解
LU分解在本質上是高斯消元法的一種表達形式。實質上是將A通過
下面以具體例子來說明。若AX=b是一個非奇異系統,
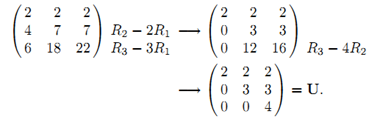
第3類行變換可以通過左乘相應的初等矩陣![]() 實現,
實現,
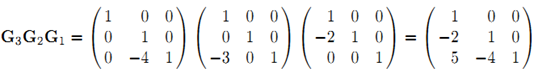 =L (2)
=L (2)
從而有![]() ,即
,即![]() 。因此A=LU,
。因此A=LU,
注意
1)U是高斯消元的結果,且對角線上是主元
2)L對角線上是1,對角線下面的元素
恰恰是在式1中用於消去(
i,j )位置上元素的乘子。
2. LDU分解
LU分解存在不對稱,因為L矩陣的主對角線元素為1,
 = DU
= DU
這就是LDU分解,其中L和U是單位三角陣(主對角線都為1),
下圖說明了Walsh matrix的LDU分解

3. LDLT分解
當A是對稱陣時,LDU分解為A=LDLT 。例子如下
對稱陣 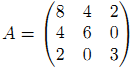 , LU分解為
, LU分解為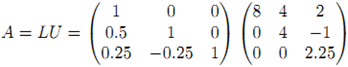 , LDLT 分解為
, LDLT 分解為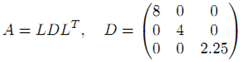 。
。
進一步,由於對角陣D的元素為正,可有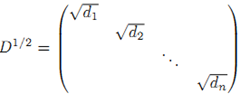 ,從而得到
,從而得到![]() ,
,
这篇关于矩陣分析-線性系統-3 LU分解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





