lcm专题

[置顶]LCM性质 + 组合数 - HDU 5407 CRB and Candies

CRB and Candies Problem's Link Mean: 给定一个数n，求LCM(C(n,0),C(n,1),C(n,2)...C(n,n))的值,(n<=1e6). analyse: 很有趣的一道数论题！看了下网上别人的做法，什么Kummer定理我还真没听说过，仔细研究一下那个鬼定理真是涨姿势了! 然而这题我并不是用Kummer那货搞的(w

Codeforces Round #328 (Div. 2)C. The Big Race（数学gcd lcm）

题目连接题意：比赛时，居然理解错题意= =，以为两个人的速度是一样的，然后有个人的只会有一步是w米，另一个人只有一步是b米。。。。就是一个人每一步是w，一个人每一步是b，终点后是深渊，然后长度是在1–t随机选择一个d作为赛道长度，问不能区分二人胜负的可能。思路：就是求d%w==d%b = = #include<bits/stdc++.h>using namespace std;

[ARC050C] LCM 111 题解

一句话题解：转化两个大数的 gcd ⁡ \gcd gcd ，再用迭代的思想求答案。 [ARC050C] LCM 111 题解题目题意给你 a a a , b b b , m m m ,其中 1 ≤ A , B ≤ 1 0 18 , 2 ≤ M ≤ 1 0 9 1\le A,B\le 10^{18},2\le M\le 10^9 1≤A,B≤1018,2≤M≤109 ，让

hdu 4497 GCD and LCM（排列组合）

题目：hdu 4497 GCD and LCM 题目大意：给出三个数的最大公约数，和最小公倍数，问这三个数的排列组合关系。解题思路：最小公倍数/最大公约数 == 三个数不同部分的乘积。这样来考虑的话，三个数都要有最大公约数的部分，其余的部分就是由LCM / GCD 里面的因子构成。这里面的因子可能会有 2 2 3 这样的情况，不同的因子之间是不会相互干扰的，但是相同的会出现问

UVA10791 - Minimum Sum LCM（分解质因子）

UVA10791 - Minimum Sum LCM（分解质因子）题目链接题目大意：给你一个N，x，y，z..(多个数)的最小公倍数是N，希望这些数的和是最小的，输出这个值（因子数至少是2）。解题思路：将N质因子分解，这样每个数其实就是每个因子的次数方，这样和一定是最小的，因为不会有可以约掉的数。1的时候要注意一下。还要需要用long long，因为当N =2147483

GCD LCM

GCD(最大公约数) 欧几里得算法(辗转相除法) 原理 if(a%b==0) GCD=b else GCD=b%(a%b) 设 a ≥ b a\ge b a≥b：若 a m o d b = = 0 a\mod b==0 amodb==0，则 g c d ( a , b ) = = b gcd(a,b)==b gcd(a,b)==b(整除性质)；若 a m o d b ! = 0 a

排数=lcm{Ai,Ai表示循环节长度},sum(Ai)=n根据lcm的定义，分解质因数拆掉Ai=p1^x1*p2^x2*...*pk^xklcm=∏(pi^max{xi})所以我们只看max{xi}即可，即忽略掉≤max{xi}的其它因子。所以问题等价于：sum(pi^xi)≤n的方案数。然后随便dp即可设d(i,j) 表示前i个质数和为j的方案，有d(i,j)=d(i−1,j)+sum(d(i

uva 11388 GCD LCM（数学：水题）

给定两个数的最大公约数和最小公倍数，问是否存在两个数a b满足条件若存在输出a最小的情况，否则输出-1 因为最小公倍数恒为最大公约数的倍数。。。所以只要满足这个条件就可以了代码如下： #include <cstdio>#include <iostream>#include <algorithm>#define LL long longusing namespace std;

ZOJ 2836 Number Puzzle 容斥、lcm

这题和HDU 1796差不多。 code： #include <cstring>#include <iostream>#include <cstdlib>#include <cstdio>#include <vector>#include <algorithm>using namespace std;typedef long long LL;const int MAXN =

HDU 1796 How many integers can you find 容斥、lcm

题意：输入n和m个数。问你小于n中，有几个数能够被m个数中的任意一个整除的。思路：容斥+lcm（最小公倍数）设m数组中结果为｛a1，a2，a3，……，am｝; 1.加上n/a1，n/a2，n/a3……的个数。 2.减去n/lcm(a1,a2)，n/lcm(a1*a3)，……，n/lcm(a2*a3)，n/lcm(a2*a4),……； 3.加上三个集合的，然后减去四个集合的，加

LCM — Least Common Multiple 最小公倍数

因为任何一个数都可以表示为若干个质数幂的乘积。比如75 = 3*5*5，即 2^0 * 3^1 * 5^2 * 7^0 ... 那么对于两个数来说，gcd就是他们取每个质数的较小幂的乘积，lcm则相反。显然，这些幂加起来就是他们乘积。 gcd(a,b) * lcm(a,b) = a*b OI Wiki: 板子： int gcd(int a, int b){if (a

hdu 4497 GCD and LCM(组合数学)

题目链接：hdu 4497 GCD and LCM 题目大意：给出三个数的最大公约数和最小公倍数，问说有多少种三个数满足。解题思路：首先用k=l/g，剩下的数即为三个中还需要存在的因子的乘积。然后将k分解成质因子；以6 72为例，k = 72/6=12，k分解成质因子为2，2，3，不同因子间肯定是互相不影响的，只要计算出每种因子的放法，相乘即为总数。现在考虑2这个因子，总

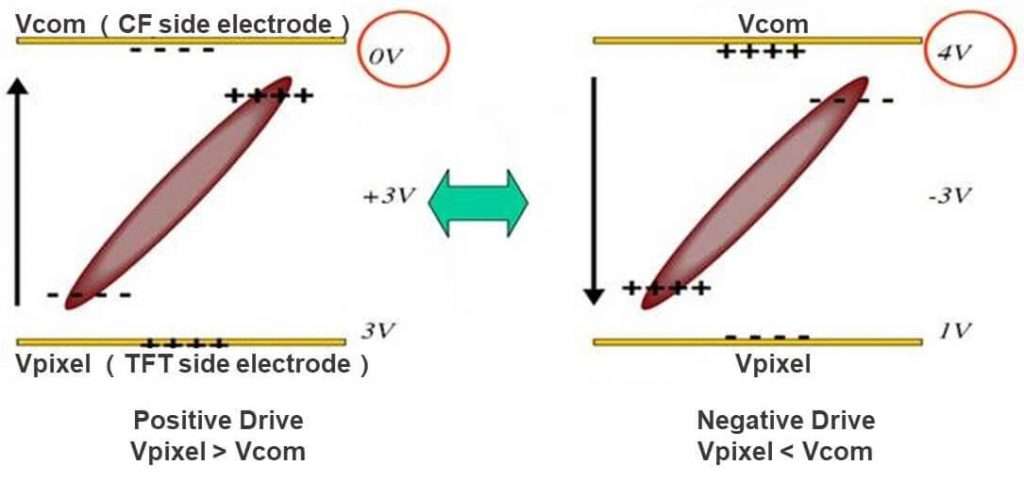
（南京观海微电子）——TFT LCM的作用

VCOM介绍 VCOM是液晶分子偏转的参考电压，要求要稳定，对液晶显示有直接影响，具体的屏不同的话也是不同的。电压的具体值是根据输入的数据以及Vcom电压大小来确定的，用来显示各种不同灰阶，也就是实现彩色显示GAMMA简单讲就是把从白色到黑色的变化过程分成2的N（6、8）次幂等份。 Gamma电压是用来控制显示器的辉阶的，一般情况下分为G0~G14，不同的Gamma

LightOJ 1236 Pairs Forming LCM

一道唯一分解的题目。代码： #include <cstdio>#include <cstring>#include <cmath>#include <iostream>#include <algorithm>using namespace std;#define maxn 10000010typedef long long LL;LL prime[1000000];bool

MTK LCM驱动移植

对于LCM驱动移植，一般分为三部曲： 1、硬件IO口配置； 2、确保LCM背光能够正常点亮； 3、LCM驱动移植；硬件电路： 1、GPIO配置打开 mediatek\dct\DrvGen.exe 选择 mediatek\custom\xiaoxi\kernel\dct\dct\codegen.dws 配置文件配置LCM PWM引脚、RST

sdutoj 3275第七届校赛--LCM的个数

题目链接：点击打开链接题目描述对于我们来说求两个数的LCM（最小公倍数）是很容易的事，现在我遇到了一个问题需要大家帮助我来解决这问题，问题是：给你一个数n，然后统计有多少对(a<=b) LCM（a,b）=n；例如LCM（a,b）=12; 即(1,12),(2,12),(3,12),(4,12),(6,12),(12,12),(3,4),(4,6)；输入输入数

java-求任意两个正整数的最大公约数和(GCD)和最小公倍数(LCM)

辗转相除法的算法为：首先将 m除以 n（m>n）得余数 r，再用余数 r 去除原来的除数，得新的余数，重复此过程直到余数为 0时停止，此时的除数就是m 和 n的最大公约数。 public class GcdLcm { public static void main(String[] args) {// TODO Auto-generated method stubint a = 377, b

基于局部对比度（LCM）的红外弱小目标检测之背景抑制

基于局部对比度（LCM）的红外弱小目标检测-Infrared Small Target Detection 1，原理参考链接：效果图 2，代码matlab版本1matlab版本2C++版本1 1，原理红外弱小目标检测跟踪算法研究参考链接： https://blog.csdn.net/Hilaryw/article/details/137232793 https://b

F. Fake Maxpooling（二维单调队列，类似筛法求lcm） 2020牛客暑期多校训练营（第二场）

题意： a [ i ] [ j ] = l c m ( i , j ) a[i][j]=lcm(i,j) a[i][j]=lcm(i,j) 求所有 k ∗ k k*k k∗k小矩阵的最大值和。思路：维护横向单调队列求每一行的前 k k k个数最值，再用纵向单调队列求出纵向前 k k k个数最值。这样求出每一点对应 k ∗ k k*k k∗k矩阵的最值了。但是本题求lcm是log，会

java求最大公约数（GCD）与最小公倍数（LCM）

求最大公约数（GCD）与最小公倍数（LCM）含义解释最大公约数（GCD）：两个或多个整数共有的约数中最大的一个。例如，12和18的最大公约数是6。对于两个非零整数a和b，它们的最大公约数是能够同时整除a和b的最大正整数。记为gcd(a, b)。最小公倍数（LCM）：两个或多个整数公有的倍数中最小的一个。例如，4和6的最小公倍数是12。对于两个非零整数a和b，它们的最小公倍数是能够同时

例题 10-4 最小公倍数的最小和（Minimum Sum LCM, UVa10791）

原题链接：https://vjudge.net/problem/UVA-10791 分类：基本数论备注：唯一分解定理又是唯一分解定理 #include <bits/stdc++.h>using namespace std;typedef long long ll;const ll maxn=1e8+5;ll n,kase,vis[maxn];vector<ll>primes;b

GCD+LCM+素数打表+快速幂【知识点】

1.最大公约数 A(51NOD 1011) 输入2个正整数A，B，求A与B的最大公约数。 Ac code:#include<iostream>using namespace std;int gcd(int a,int b)//最大公约数 {return b?gcd(b,a%b):a;}int main(){int a,b;cin>>a>>b;cout<<gcd(a,

T-GATE 无需要训练加速diffusion模型； PixArt-Alpha LCM再加速使用

参考：https://github.com/HaozheLiu-ST/T-GATE git clone https://github.com/HaozheLiu-ST/T-GATE.git transformers 4.38torch 2.1.2+cu118 代码： inference_step 4-10高点效果会好点，这步数比原来20来

数学矩阵GCD和lCM（详解）

矩阵乘法知阵乘法是《线性代数》中的基础内容，但在考察数学的算法题中也会出现。本节我们学习基础的矩阵乘法规则。每个矩阵会有一个行数和一个列数，只有当相乘的两个矩阵的左矩阵的列数等于右矩阵的行数时，才能相乘，否则不允许做矩阵乘法。例如，3x5的矩阵可以和5x7的矩阵做乘法，但是3x5的阵不能和4x7的矩阵做乘法N*M的知阵利M*K的矩阵做乘法后的矩阵大小为N*K 矩阵乘法的规则用一句话描述

UVa 10892 LCM Cardinality (数论+组合数学)

UVa 10892 LCM Cardinality 题目大意: 输入正整数 n n(n≤2∗109n \leq 2*10^9),统计有多少对正整数 a≤b a \leq b,满足 lcm(a,b)=n lcm(a,b)=n.输出n和形成的对数. 题目分析: (想了好一会儿,orz……) 若将数拆分成唯一分解式,可以发现设 a=pk11∗pk22∗...∗pknnb=pk′11∗

H - Pairs Forming LCM

题目链接：https://cn.vjudge.net/contest/70017#problem/H 题目大意：给你一个数ｎ，让你在ｎ中找一对ａ，ｂ两个值且a<b，使得ａ和b的最大公倍数是ｎ。题解：唯一分解定理，把每一个ａ和ｂ分解成以素数为因子的乘积（算数基本定理那样），需要取每一个素数因子的指数最大的那素因子然后相乘，使得到的数为ｎ。例如a=a1^e1*a2^e2.........ax