本文主要是介绍数学矩阵GCD和lCM(详解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
矩阵乘法
知阵乘法是《线性代数》中的基础内容,但在考察数学的算法题中也会出现。
本节我们学习基础的矩阵乘法规则。
每个矩阵会有一个行数和一个列数,只有当相乘的两个矩阵的左矩阵的列数等于右矩阵的行数
时,才能相乘,否则不允许做矩阵乘法。
例如,3x5的矩阵可以和5x7的矩阵做乘法,但是3x5的阵不能和4x7的矩阵做乘法N*M的知阵利M*K的矩阵做乘法后的矩阵大小为N*K
矩阵乘法的规则用一句话描述就是,第一个矩阵A的第i行和第二个矩阵B的第i列的各M个元素对应相乘再相加得到新矩阵C[i][j]的值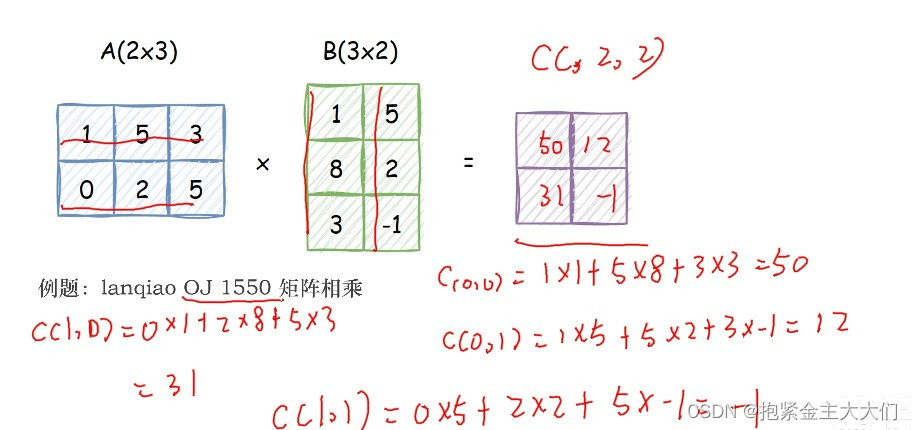
例题
矩阵相乘
题目描述
小明最近刚刚学习了矩阵乘法,但是他计算的速度太慢,于是他希望你能帮他写一个矩阵乘法的运算器。
输入描述
输入的第一行包含三个正整数 N,M,K,表示一个 $NM的矩阵乘以一个的矩阵乘以一个MK的矩阵。接下来N行,每行M个整数,表示第一个矩阵。再接下来的M行,每行K$ 个整数,表示第二个矩阵。
0<<N,M,K≤100, 0≤ 矩阵中的每个数 ≤1000
输出描述
输出有 N 行,每行 K 个整数,表示矩阵乘法的结果。
输入输出样例
示例
输入
2 1 3
1
2
1 2 3
输出
1 2 3
2 4 6package shuxeu;
import java.util.*;
public class juzhen {public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);int m=scan.nextInt();int n=scan.nextInt();int k=scan.nextInt();int [][]a=new int[m][n];int [][]p=new int[n][k];for(int i=0;i<m;i++) {for(int j=0;j<n;j++) {a[i][j]=scan.nextInt();}}for(int i=0;i<n;i++) {for(int j=0;j<k;j++) {p[n][k]=scan.nextInt();}}int[][]sum=new int[m][k];for(int i=0;i<m;i++) {for(int j=0;j<k;j++) {for(int c=0;c<n;c++) {sum[i][j]+=a[i][c]*p[c][j]; }System.out.println(sum[i][j]);}System.out.println("");}}}
整除
在计算机中,整数之间的除法往往是整除且向下取整的

同余
同余是数论中非常重要的概念,意思是两个或多个数字x,对于一个模数M的余数是相等的
或者说在模M意义下,他们是相等的。
例如当M=7,x=[1,8,15,8,50]是同余的,这些x有一个共同的关系,就是x%M=1。
GCD和LCM
GCD( Greatest Common Divisor) 是最大公约数,LCM(Least Common Multiple) 是最小公倍数。大多数情况下,我们更关注GCD如果题口和LCM有关,也通常会转换成和GCD相关的。
gcd通过欧几里得辗转相除法得到,同样,初次学习不必过于深究其原理,学会使用最重要lcm通过gcd(x,y)*lcm(x,y)=x*y来得到。
gcd欧几里得辗转相除法
public int gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
简单地理解一下,首先不妨设a<b,有gcd(a,b)=gcd(a,b-a)=gcd(a,b-2a)...=gcd(a,b%a),又有
b%a<a,于是将他们两个调换位置,继续向下递归,直到b变为0,gcd(x,0)=x。
LCM求解方法
public int lcm(int a,int b){
return a/gcd(a,b)*m;
}
推荐先做除法,再做乘法,避免溢出。
例题
最大公约数
题目描述
给定两个正整数A,B,求它们的最大公约数。
输入描述
第 1 行为一个整数 T,表示测试数据数量。
接下来的 T 行每行包含两个正整数 A,B。
1≤T≤10^5,1≤A,B≤10^9。
输出描述
输出共 T 行,每行包含一个整数,表示答案。
输入输出样例
示例 1
输入
5
2 4
3 7
5 10
6 8
7 9
输出
2
1
5
2
1package gcd;
import java.util.*;
public class chapter1 {public static void main(String[] args) {// TODO Auto-generated method stubScanner scan=new Scanner(System.in);long T=scan.nextLong();while(T-->0) {long A=scan.nextLong();long B=scan.nextLong();long sum=gcd(A,B);System.out.println(sum);}}private static long gcd(long a, long b) {// TODO Auto-generated method stubreturn b==0?a:gcd(b,a%b);}}
这篇关于数学矩阵GCD和lCM(详解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





