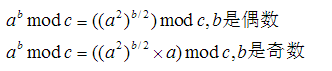GCD+LCM+素数打表+快速幂【知识点】

本文主要是介绍GCD+LCM+素数打表+快速幂【知识点】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 

1.最大公约数

A(51NOD 1011)

输入2个正整数A，B，求A与B的最大公约数。

 

Ac code:
#include<iostream>
using namespace std;
int gcd(int a,int b)//最大公约数 
{return b?gcd(b,a%b):a;
}
int main()
{int a,b;cin>>a>>b;cout<<gcd(a,b)<<endl;return 0;
}

求法推演

首先考虑一下：

对于任意两个正整数 a,ba,b ，都有：

a=kb+ra=kb+r

(k,r∈N)(k,r∈N)

所以有：

r=a%b

（在这里，%指的是取余运算）

然后我们假设 cc 是 aa 和 bb 的最大公约数，即

c=gcd(a,b)

然后，我们就能得到：

c|a

c|b

（在这里当然包括除了在这里的任何地方，a|b 表示 bb 能够整除 aa）

然后又因为上面那个式子，有：

r=a−kb

所以有：

c|r

整合一下上面的式子，我们可以得到：

c=gcd(b,r)

即

gcd(a,b)=gcd(b,a%b)

代码（递归）

int gcd(int a,int b)
{if(b==0) return a;return gcd(b,a%b);
}

这种写法就是辗转相除法。

当然为了防止某些情况爆栈（比如说高精度运算什么的），还可以不用递归来写。。。

代码（迭代）

int gcd(int a,int b)
{while(b){a=a%b;swap(a,b);}return a;
}

当然本质上这两种计算方式是一样的

2.最小公倍数

B(51NOD1012)

输入2个正整数A，B，求A与B的最小公倍数。

*int会wa

AC code:
#include<iostream>
using namespace std;
long long gcd(long long a,long long b)//最大公约数 
{return b?gcd(b,a%b):a;
}
int main()
{long long a,b;cin>>a>>b;cout<<a*b/gcd(a,b)<<endl;return 0;
}

4.快速幂

定义：

快速幂顾名思义，就是快速算某个数的多少次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高。

快幂算法1

这里我们需要两个公式：

 

这两个公式都不难理解，自己可以验证一下，3^4 = 9^2。

有了这两个公式之后我们就可以考虑思路了。

我们就以b为偶数来举例。

a^b%c = ((a^2)^b/2)%c;

在这里我们假设b/2还是偶数，那么

((a^2)^b/2)%c = (((a^2)^2)^(b/2)/2)%c;到这里就可以了.

 

 

快速幂算法2

它的原理如下：

　　假设我们要求a^b，那么其实b是可以拆成二进制的，该二进制数第i位的权为2^(i-1)，例如当b==11时

　　　　　　　　　　　　　　　　　　　　　　　　　　 

　　11的二进制是1011，11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1，因此，我们将a¹¹转化为算 a2^0*a2^1*a2^3，也就是a1*a2*a8 

，看出来快的多了吧原来算11次，现在算三次。                                                                                           

　　由于是二进制，很自然地想到用位运算这个强大的工具：&和>>    

&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇。

>>运算比较单纯,二进制去掉最后一位

 

 

ll bin_pow(ll a, ll b)
{ll ans = 1;while (b > 0) {if (b&1) //奇数 {s = s * a;}a = a * a;b = b >> 1;}return ans;
}

 常规求幂int pow1(int a,int b){int r=1;while(b--) r*=a;return r;
} 快速求幂（一般）int pow2(int a,int b){int r=1,base=a;while(b!=0){if(b%2) r*=base;base*=base;b/=2;}return r;
}快速求幂 （递归）
int f(int m,int n){   //m^nif(n==1) return m;int temp=f(m,n/2);return (n%2==0 ? 1 : m)*temp*temp;
}快速求幂（位运算）
int pow3(int x,int n){if(n==0) return 1;else {while((n&1)==0){n>>=1;x*=x;}}int result=x;n>>=1;while(n!=0){x*=x;if(n&1) result*=x;n>>=1;}return result;
}快速求幂（位运算，更简洁）
int pow4(int a,int b){int r=1,base=a;while(b){if(b&1) r*=base;base*=base;b>>=1;}return r;
}

补充：C语言中移位运算符

位移位运算符是将数据看成二进制数，对其进行向左或向右移动若干位的运算。位移位运算符分为左移（<<）和右移(>>)两种，均为双目运算符。第一运算对象是移位对象，第二个运算对象是所移的二进制位数。

左移运算是将一个二进制位的操作数按指定移动的位数向左移位，移出位被丢弃，右边的空位一律补0。右移运算是将一个二进制位的操作数按指定移动的位数向右移动，移出位被丢弃，左边移出的空位或者一律补0，或者补符号位，这由不同的机器而定。在使用补码作为机器数的机器中，正数的符号位为0，负数的符号位为1。

这篇关于GCD+LCM+素数打表+快速幂【知识点】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---