cdq专题
【COGS】577 蝗灾 cdq分治
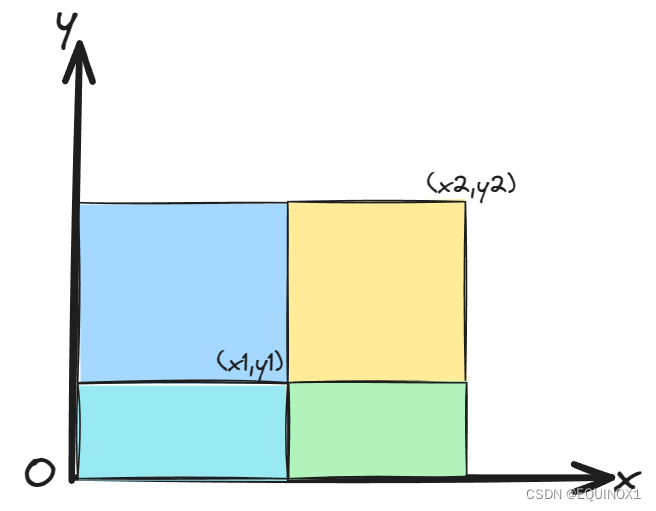
传送门:【COGS】577 蝗灾 题目分析:cdq分治入门题= =。。。。用差分思想将矩阵分成四块来计算。。排序一维,另一维用树状数组解决。 代码如下: #include <cstdio>#include <vector>#include <cstring>#include <algorithm>using namespace std ;#define REP(
【ACdream】1157 Segments cdq分治
传送门:【ACdream】1157 Segments 题目分析:第一题cdq(陈丹琦)分治!cdq_____Orz! 听说cdq分治可以写,就去学了cdq分治了。。 在我们平常使用的分治中,每一个子问题只解决它本身(可以说是封闭的)。 而在cdq分治中,对于划分出来的两个子问题,前一个子问题用来解决后一个子问题而不是它本身。 具体算法流程如下: 1.将整个操作序列分为两个长
【ZOJ】3874 Permutation Graph 【FFT+CDQ分治】
传送门:【ZOJ】3874 Permutation Graph 题目分析: 容易知道一个个连通块内部的标号都是连续的,否则一定会有另一个连通块向这个连通块建边,或者这个连通块向另一个连通块建边。而且从左到右左边的连通块内最大的标号小于右边连通块内最小的标号。 然后我们可以构造dp方程: dp[n]=n!−i!∗dp[n−i] \qquad \qquad dp[n] = n! - i! *
HDU 4456 Crowd (cdq分治)
大意就是给出一个矩阵 初始每个位置上的值都为0 然后有两种操作 一种是更改某个位置上的值 另一个是求某个位置附近曼哈顿距离不大于K的所有位置的值的总和 网络上众多题解都是 二维树状数组 但是这题也被认为是cdq分治的基础题 下面提供两种基于cdq分治的解法 解法一: 将所有点绕原点左旋45° 然后新的坐标也很好计算 x'
[Uva 11990] Dynamic Inversion (CDQ分治入门)
Uva - 11990 动态逆序对,求删除一个点之前序列中逆序对的个数 首先倒过来看这个问题,把点先全部删掉 然后从最后一个点开始倒着往数列中加点 求加完这个点逆序对的变化 CDQ分治做法 把删除时间看作 t,下标看作 x,值看作 y 然后对 x排序,对 t偏序,用树状数组维护 y 具体来说就是对于每个点 (t0,x0,y0) (t_0, x_0, y_0) 先统计
深入理解归并排序——从归并排序到CDQ分治、归并树
归并排序 首先考虑下如何将将二个有序数列合并。这个非常简单,只要从比较二个数列的第一个数,谁小就先取谁。然后再进行比较,如果有数列为空,那直接将另一个数列的数据依次取出即可。 //将有序数组a[]和b[]合并到c[]中 void merge(int a[], int n, int b[], int m, int c[]) {int i, j, k; i = j = k = 0; whi
CDQ分治维护凸包 优化dp 【NOI2007】货币兑换cash bzoj1492
题目描述: 小 Y 最近在一家金券交易所工作。该金券交易所只发行交易两种金券:A 纪 念券(以下简称 A 券)和 B 纪念券(以下简称 B 券)。每个持有金券的顾客都有 一个自己的帐户。金券的数目可以是一个实数。 每天随着市场的起伏波动,两种金券都有自己当时的价值,即每一单位金券 当天可以兑换的人民币数目。我们记录第 K 天中 A 券和 B 券的价值分别为 AK 和 BK (元/单位金
[BZOJ3262] 陌上花开 —— CDQ三维分治
Description 有n朵花,每朵花有三个属性:花形(s)、颜色©、气味(m),用三个整数表示。 现在要对每朵花评级,一朵花的级别是它拥有的美丽能超过的花的数量。 定义一朵花A比另一朵花B要美丽,当且仅Sa>=Sb,Ca>=Cb,Ma>=Mb。 显然,两朵花可能有同样的属性。需要统计出评出每个等级的花的数量。 Input 第一行为N,K (1 <= N <= 100,000, 1 <= K <
bzoj4700 适者 CDQ分治+斜率优化毒瘤题
题目链接:传送门 对于每个敌方的人形兵器,记录一个 B B B,表示多少次能够打死这个人形兵器。 易知 B i = ⌈ D i A T K ⌉ B_i=\lceil\frac{D_i}{ATK}\rceil Bi=⌈ATKDi⌉。 首先考虑没有秒杀的情况: 显然应该按照某个顺序打死所有人形兵器(不可能打人形兵器A打到一半突然开始打B),所以考虑什么时候交换人形兵器 i , i + 1 i,
LOJ #2483 [CEOI2017]Building Bridges CDQ分治+斜率优化
题目链接:传送门 洛咕传送门 令 s u m w sumw sumw表示 w w w的前缀和。 显然的 d p dp dp方程: d p [ i ] = m i n ( d p [ j ] + ( h [ i ] − h [ j ] ) 2 + s u m w [ i − 1 ] − s u m w [ j ] ) dp[i]=min(dp[j]+(h[i]-h[j])^2+sumw[i-1]-
bzoj2726 洛谷P2365 [SDOI2012]任务安排 cdq分治+斜率优化
题目链接: bzoj2726 洛谷2365 洛咕上好像 O ( n 2 ) O(n^2) O(n2)能过……还没有负数的情况…… 如果没有负数,就直接大莉上斜率优化就珂以了qwq 转移方程是 d p [ i ] = d p [ j ] + s u m T [ i ] ∗ ( c [ i ] − c [ j ] ) + S ∗ ( c [ n ] − c [ j ] ) dp[i]=dp[j]+s
分治、CDQ分治小结
分治、CDQ分治小结 A Summary for Divide and Conquer 0. Anouncement 本文部分图片以及部分内容来自互联网,内容过多就不一一注明出处了,冒犯之处还请海涵。 Some of the pictures and the content of the text come from the Internet. Due to plenty of th
分治算法,逆序对,三维偏序与CDQ分治
分治算法基本思想 当我们求解某些问题时,由于这些问题要处理的数据相当多,或求解过程相当复杂,使得直接求解法在时间上相当长,或者根本无法直接求出。 对于这类问题,我们往往先把它分解成几个子问题,找到求出这几个子问题的解法后,再找到合适的方法,把它们组合成求整个问题的解法。 如果这些子问题还较大,难以解决,可以再把它们分成几个更小的子问题,以此类推,直至可以直接求出解为止。这就是分治策略的基本思
P3810 三维偏序 cdq分治
题目背景https://www.luogu.org/problemnew/show/P3810 这是一道模板题 可以使用bitset,CDQ分治,K-DTree等方式解决。 题目描述 输入输出样例 输入样例#1: 复制 10 33 3 32 3 32 3 13 1 13 1 21 3 11 1 21 2
CDQ分治详解,一维、二维、三维偏序
文章目录 零、偏序关系一、一维偏序二、二维偏序三、三维偏序(CDQ)3.1CDQ分治3.2CDQ分治解决三维偏序的流程 四、OJ练习4.1三维偏序模板题4.1.1原题链接4.1.2AC代码 4.2老C的任务4.2.1原题链接4.2.2解题思路4.2.3AC代码 4.3动态逆序对4.3.1原题链接4.3.2解题思路4.3.3AC代码 零、偏序关系 设R是集合A上的一个关系
关于查询区间最小没出现的自然数的cdq方法的可行性探讨
这道题显然有一个可持久化线段树的做法。 首先我们意识到这个极广的值域没有什么用处。 我们首先想到必然存在一个 x \ x x使答案为 x \ x x或者 [ 1 , x − 1 ] \ [1,x-1] [1,x−1]中的最小的不存在的数字。 所以首先我们想到找到这个 x \ x x然后把没有必要的数字全部删掉,这样剩下的数字必然再 [ 1 , n ] \ [1,n] [1,n]中。
天使玩偶 [CDQ分治]
传送门 我们可以将这些操作看成(x,y,t) 三元组 , 表示x,y坐标 , 与时间 CDQ 分治时 将前一半时间的修改提出来 , 再将后一半时间的询问提出来 然后按x 排序 , 这样就是一个二维偏序了 , 但是有一个问题 , 我们如何求dis 发现可以分4种情况 , 这里拿左下举个例子 我们发现 于是 x 按顺序插入 , 在树状数组的y 的位置插入(xi + yi) , 询问就是x
【CDQ分治】三维偏序(luogu 3801/金牌导航 CDQ分治-1)
三维偏序 luogu 3801 金牌导航 CDQ分治-1 题目大意 有n个元素,第i个元素有 a i , b i , c i a_i,b_i,c_i ai,bi,ci三个属性,设 f(i)表示满足 a j ⩽ a i a_j\leqslant a_i aj⩽ai且 b j ⩽ b i b_j \leqslant b_i bj⩽bi且 c j ⩽ c i c_j \leqsla
[BZOJ 2253][2010 Beijing wc]纸箱堆叠:CDQ分治|DP
点击这里查看原题 首先这是一个严格三维偏序问题,可以用CDQ分治来做,其次这又是一个三维的最长上升子序列问题,dp[i]表示以第i个箱子为结尾的最长长度。 于是我们先将所有箱子按x大小排序,因为要严格上升,因此对于x值相等的情况我们要微调mid的位置,确保x值相等的箱子在一个分治区间内。在每个分治区间内又按y大小排序,对左区间用树状数组维护前缀最大值,对右区间查询前缀最大值。 /*User
[BZOJ 1492][NOI2007]货币兑换Cash:CDQ分治|DP斜率优化
点击这里查看原题 首先贪心的想,每次买卖必然要买空或者卖空,因为有便宜就尽量去占,于是可以得到方程: f[i]=max{f[j]/(a[j]*rate[j]+b[j])*rate[j]*a[i]+f[j]/(a[j]*rate[j]+b[j])*b[i]} 其中,x[j]=f[j]/(a[j]*rate[j]+b[j])*rate[j]表示第j天最多可以拥有的A货币的数量,y[j]=f
[BZOJ 4237]稻草人:CDQ分治
点击这里查看原题 这个CDQ分治需要首先按Y坐标排序,然后每个递归处理的区间内按X坐标排序。每次从右区间加入一个点则将左区间所有X坐标小于该点的点加入,维护两个单调栈,左区间的是Y坐标递减的栈,右区间是Y坐标单调递增的栈。这样每次加入右区间的点时答案就是 (左区间的栈中的元素数-左栈中Y坐标小于右区间上一个点的Y坐标的点数) 有点拗口,具体看代码,用二分搜索得到左栈中Y坐标小于右
Codevs 1080 线段树练习(线段树树状数组分块CDQ分治)
1080 线段树练习 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 传送门 题目描述 Description 一行N个方格,开始每个格子里都有一个整数。现在动态地提出一些问题和修改:提问的形式是求某一个特定的子区间[a,b]中所有元素的和;修改的规则是指定某一个格子x,加上或者减去一个特定的值A。现在要求你能对每个提问作出正确的回答。1≤N<
[BZOJ3262]陌上花开 CDQ+树状数组
三维的有序 第一维排序 第二维CDQ 第三维树状数组 注意要把完全相同的两个点合在一起 他们都互相比对方美丽 #include<cstdio>#include<algorithm>#include<cstring>#include<iostream>#include<queue>#define SF scanf#define PF printf#define lowbit(
[BZOJ3295] [Cqoi2011]动态逆序对 CDQ分治
CDQ跑的比分治快得多 首先 我们可以把每一个点看成一个三元组(x, y, z) x 表示它当前的值 y 表示的在序列中的编号 z 表示它的时间 即第z次操作后的这个点 所以 如果某个点P在平面上的左上方有点(值小于P并且位置在P之后) 后者右下方(恰好相反)的地方有点 就会形成一个逆序对 在一开始我们很容易求出每一个点形成的逆序对总数 每次删除的时候从ans中减去 然而 在CDQ分治的过
[BZOJ1492][NOI2007]货币兑换Cash CDQ分治+斜率优化
这种分治思想我也是醉了Orz 首先对于这道题 我们可以发现 如果某一天你要买进或卖出 那一定是尽可能的买或卖 那么我们就可以用一个状态f[i]表示某一天的最大收益 那么就有 f[i] = (rate[j] * f[j] * a[i] + f[j] * b[i]) / (rate[i] * a[i] + b[i] 那么朴素转移就很容易了 怎样优化呢 令 y[j] = f[j] / (r