CDQ分治详解，一维、二维、三维偏序

2024-02-27 05:52
文章标签 详解 三维 分治 二维 一维 cdq 偏序

本文主要是介绍CDQ分治详解，一维、二维、三维偏序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

    • 零、偏序关系
    • 一、一维偏序
    • 二、二维偏序
    • 三、三维偏序(CDQ)
      • 3.1CDQ分治
      • 3.2CDQ分治解决三维偏序的流程
    • 四、OJ练习
      • 4.1三维偏序模板题
        • 4.1.1原题链接
        • 4.1.2AC代码
      • 4.2老C的任务
        • 4.2.1原题链接
        • 4.2.2解题思路
        • 4.2.3AC代码
      • 4.3动态逆序对
        • 4.3.1原题链接
        • 4.3.2解题思路
        • 4.3.3AC代码

零、偏序关系

设R是集合A上的一个关系，如果R是自反的、反对称的、传递的，则称R为一个偏序关系(或称部分序关系、半序关系)。

通常，将偏序关系R写做≤，读做“小于或等于”。
对于一维、二维、三维我们有着不同的处理手段。

一、一维偏序

给你一个长度为n的序列，求出每个元素在序列中比其小的元素数目。

这是最为简单的偏序问题，处理方法也很简单：将原序列升序排序，当然如果有重复元素，我们要适当进行去重处理。

二、二维偏序

有n个元素，第i个元素有ai,bi两个属性,求出每个下标i，满足j != i，aj ≤ ai且bj ≤ bi的j的数目

基本思路：按照第一维排序，然后计算前一半对于后一半的影响。

基于这样的思路，我们有两种做法：

F1归并排序

和归并排序计算逆序对很像

  • 先按照ai进行排序，然后对bi进行归并排序
  • 归并排序时，序列被划分为[l, mid]和[mid + 1, r]两个序列
  • 虽然按照bi进行归并排序会导致ai的顺序混乱，但是两个序列仍然满足左边序列的ai不大于右边序列的ai
  • 当我们双指针合并两个序列时，当要存放右边序列的元素时，可以根据左边指针和左边界的相对位置计算其贡献
  • 时间复杂度O(nlogn)

F2树状数组

  • 先按照ai进行排序，然后开树状数组维护当前遍历位置之前值小于等于bi的元素数目
  • 遍历按照第一维排序后的序列，ans[i] = query(b[i])
  • 时间复杂度O(nlogn)

代码十分简单，这里不再给出

三、三维偏序(CDQ)

有n个元素，第 i个元素有ai，bi，ci三个属性，设 f(i) 表示满足 aj ≤ ai且 bj ≤ bi 且 cj ≤ ci且 j != i 的 j 的数量。

对于d ∈ [0, n) ，求 f(i) = d 的i数量。

虽然问题变成了三维偏序，但是基本思路还是按照某个维度排序，然后计算前面对后面的影响，通过这样的策略，达到将问题降维的效果。

3.1CDQ分治

CDQ分治是以曾经的IOI选手陈丹琦命名的一种离线的分治算法，主要用于解决偏序问题。

3.2CDQ分治解决三维偏序的流程

同样有归并排序和树状数组两种做法，我们这里给出树状数组做法。

  • 先按一维属性排序和去重
    1.假设三维分别是x，y，z，先按x排序。
    2.然后去掉重复元素，记录每个元素出现的次数cnt
  • CDQ分治：类似归并排序的思想，先按第一维属性划分为前一半和后一半，回归时计算前一半对后一半的影响
  1. 分治后每次将前一半、后一半分别按y排序。虽然现在x的顺序被打乱了，但是前一半的x还是都小于后一半的，所以只计算前一半对后一半的偏序关系，是不会受到x影响的。
  2. 用双指针 i,j来维护前一半和后一半，每次将j后移一位时，若y[i] <= y[j]，则不断后移i，并不断将z[i]加入树状数组。然后再查询树状数组中有多少数<=z[j]，即<= e[j]的偏序数量。
  3. 最后要清空树状数组。
    时间复杂度O(nlog^2n)

四、OJ练习

4.1三维偏序模板题

4.1.1原题链接

P3810 【模板】三维偏序（陌上花开） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

4.1.2AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 100005, K = 200005;
int n, k, tot = 0;
int ans[N], tr[K];struct node
{int a, b, c, s = 1, res;bool operator==(const node &x) const{return a == x.a && b == x.b && c == x.c;}
} nodes[N];bool cmpa(const node &x, const node &y)
{if (x.a != y.a)return x.a < y.a;if (x.b != y.b)return x.b < y.b;return x.c < y.c;
}
bool cmpb(const node &x, const node &y)
{if (x.b != y.b)return x.b < y.b;return x.c < y.c;
}
void modify(int x, int v)
{for (; x <= k; x += (x & -x))tr[x] += v;
}
int query(int x)
{int res = 0;for (; x > 0; x &= (x - 1))res += tr[x];return res;
}
void CDQ(int l, int r)
{if (l == r)return;int mid = (l + r) >> 1;CDQ(l, mid), CDQ(mid + 1, r);sort(nodes + l, nodes + mid + 1, cmpb), sort(nodes + mid + 1, nodes + r + 1, cmpb);int i = l, j = mid + 1;for (; j <= r; j++){for (; i <= mid && nodes[i].b <= nodes[j].b; i++)modify(nodes[i].c, nodes[i].s);nodes[j].res += query(nodes[j].c);}for (j = l; j < i; j++)modify(nodes[j].c, -nodes[j].s);
}
int main()
{freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> k;for (int i = 1; i <= n; i++)cin >> nodes[i].a >> nodes[i].b >> nodes[i].c;sort(nodes + 1, nodes + n + 1, cmpa);for (int i = 1; i <= n; i++){if (nodes[i] == nodes[tot])nodes[tot].s++;elsenodes[++tot] = nodes[i];}CDQ(1, tot);for (int i = 1; i <= tot; i++)ans[nodes[i].s + nodes[i].res - 1] += nodes[i].s;for (int i = 0; i < n; i++)cout << ans[i] << '\n';return 0;
}

4.2老C的任务

4.2.1原题链接

[P3755 CQOI2017] 老C的任务 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

4.2.2解题思路

对于每个询问，我们要计算出矩形区域内的基站数目，数据范围允许的情况下自然可以用二维前缀和进行快速计算

但是我们发现二位前缀和维护的无非是两个维度都不超过自己的点的数目，这样我们可以用二维偏序解法计算出每个点其左下角的点的数目，这样相当于变相计算出了二维前缀和

那么对于x1，y1，x2，y2的查询，显然有ans = pre[x2][y2] - pre[x2][y1 - 1] - pre[x1 - 1][y2] + pre[x1 - 1][y1 - 1]

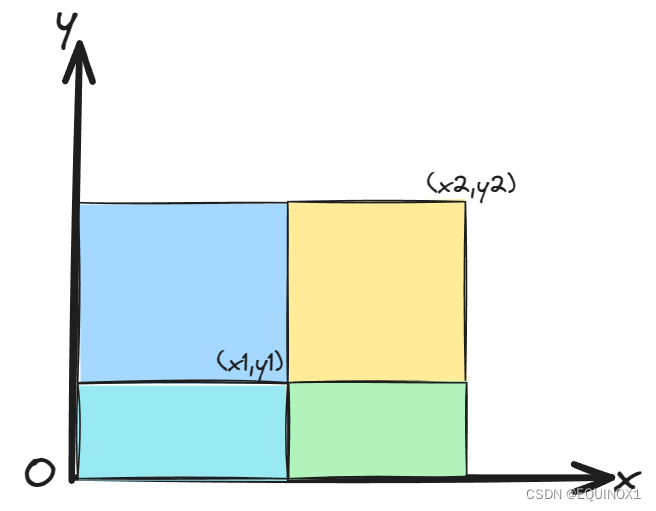
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

那么是否可以转化为三维偏序问题求解呢？

对于查询的点，我们都给其增加一个维度，然后加入序列，这样CDQ求出的查询点的二位前缀和，我们给要减去前缀和的点一个-1，加上的给一个1，方便后序计算答案

4.2.3AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5e5 + 10;
struct node
{int a, b, c, s, id, sign;long long res;bool operator==(const node &x) const{return a == x.a && b == x.b && c == x.c;}
} nodes[N];
int n, m;
long long ans[N], tr = 0;
bool cmpa(const node &x, const node &y)
{if (x.a != y.a)return x.a < y.a;if (x.b != y.b)return x.b < y.b;return x.c < y.c;
}
bool cmpb(const node &x, const node &y)
{if (x.b != y.b)return x.b < y.b;return x.c < y.c;
}
void CDQ(int l, int r)
{if (l == r)return;int mid = (l + r) >> 1;CDQ(l, mid), CDQ(mid + 1, r);sort(nodes + l, nodes + mid + 1, cmpb), sort(nodes + mid + 1, nodes + r + 1, cmpb);int i = l, j = mid + 1;for (; j <= r; j++){for (; i <= mid && nodes[i].b <= nodes[j].b; i++)tr += !nodes[i].c * nodes[i].s;if (nodes[j].c)nodes[j].res += tr;}for (j = l; j < i; j++)tr -= !nodes[j].c * nodes[j].s;
}
int main()
{// freopen("in.txt", "r", stdin);ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> m;for (int i = 1; i <= n; i++)cin >> nodes[i].a >> nodes[i].b >> nodes[i].s;for (int i = 1, a1, b1, a2, b2; i <= m; i++){cin >> a1 >> b1 >> a2 >> b2;nodes[++n] = {a2, b2, 1, 0, i, 1};nodes[++n] = {a1 - 1, b1 - 1, 1, 0, i, 1};nodes[++n] = {a2, b1 - 1, 1, 0, i, -1};nodes[++n] = {a1 - 1, b2, 1, 0, i, -1};}sort(nodes + 1, nodes + 1 + n, cmpa);CDQ(1, n);for (int i = 1; i <= n; i++)if (nodes[i].c)ans[nodes[i].id] += nodes[i].res * nodes[i].sign;for (int i = 1; i <= m; i++)cout << ans[i] << '\n';return 0;
}

4.3动态逆序对

4.3.1原题链接

[P3157 CQOI2011] 动态逆序对 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

4.3.2解题思路

该问题和普通逆序对相比只多了一个维度——时间

那么我们将原序列元素的删除时间设置为0，删除元素删除时间从1到m依次增加，这样一来我们要求的点对即为：

ti < tj, pi < pj, vi > vj或者ti < tj, pi > pj, vi < vj

这样CDQ中我们要跑两次双指针，清空两次树状数组

对于删除元素修改树状数组的贡献我们设置为-1，原序列为1

这样就巧妙的解决了问题

4.3.3AC代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
const int N = 1e5 + 10, M = 5e4 + 10;
struct node
{int t, p, v, k;
} nodes[N + M];
int ans[M], tr[N];
int mp[N], n, m, tot = 0;
int query(int x)
{long long res = 0;for (; x > 0; x &= (x - 1))res += tr[x];return res;
}
void modify(int x, int v)
{for (; x <= n; x += (x & -x))tr[x] += v;
}
bool cmp(const node &x, const node &y)
{return x.p < y.p;
}
void CDQ(int l, int r)
{if (l == r)return;int mid = (l + r) >> 1;CDQ(l, mid), CDQ(mid + 1, r);sort(nodes + l, nodes + mid + 1, cmp), sort(nodes + mid + 1, nodes + 1 + r, cmp);int i = l, j = mid + 1;for (; j <= r; ++j){for (; i <= mid && nodes[i].p < nodes[j].p; ++i)modify(nodes[i].v, nodes[i].k);ans[nodes[j].t] += (query(n) - query(nodes[j].v)) * nodes[j].k;}for (j = l; j < i; j++)modify(nodes[j].v, -nodes[j].k);i = mid, j = r;for (; j > mid; --j){for (; i >= l && nodes[i].p > nodes[j].p; --i)modify(nodes[i].v, nodes[i].k);ans[nodes[j].t] += query(nodes[j].v - 1) * nodes[j].k;}for (j = mid; j > i; j--)modify(nodes[j].v, -nodes[j].k);
}
signed main()
{ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);//freopen("in.txt", "r", stdin);//freopen("out.txt", "w", stdout);cin >> n >> m;for (int i = 1, x; i <= n; ++i)cin >> x, mp[x] = i, nodes[++tot] = {0, i, x, 1};for (int i = 1, x; i <= m; ++i)cin >> x, nodes[++tot] = {i, mp[x], x, -1};CDQ(1, tot); // CDQ分治for (int i = 1; i <= m; ++i)ans[i] += ans[i - 1]; // 前缀和for (int i = 0; i < m; ++i)cout << ans[i] << '\n';return 0;
}

这篇关于CDQ分治详解，一维、二维、三维偏序的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/751395。

相关文章

Linux换行符的使用方法详解

Linux换行符的使用方法详解

《Linux换行符的使用方法详解》本文介绍了Linux中常用的换行符LF及其在文件中的表示,展示了如何使用sed命令替换换行符,并列举了与换行符处理相关的Linux命令,通过代码讲解的非常详细,需要的... 目录简介检测文件中的换行符使用 cat -A 查看换行符使用 od -c 检查字符换行符格式转换将
阅读更多...
详解C#如何提取PDF文档中的图片

详解C#如何提取PDF文档中的图片

《详解C#如何提取PDF文档中的图片》提取图片可以将这些图像资源进行单独保存,方便后续在不同的项目中使用,下面我们就来看看如何使用C#通过代码从PDF文档中提取图片吧... 当 PDF 文件中包含有价值的图片，如艺术画作、设计素材、报告图表等，提取图片可以将这些图像资源进行单独保存，方便后续在不同的项目中使
阅读更多...
Android中Dialog的使用详解

Android中Dialog的使用详解

《Android中Dialog的使用详解》Dialog（对话框）是Android中常用的UI组件,用于临时显示重要信息或获取用户输入,本文给大家介绍Android中Dialog的使用,感兴趣的朋友一起... 目录android中Dialog的使用详解1. 基本Dialog类型1.1 AlertDialog（
阅读更多...
C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
Java中StopWatch的使用示例详解

Java中StopWatch的使用示例详解

《Java中StopWatch的使用示例详解》stopWatch是org.springframework.util包下的一个工具类,使用它可直观的输出代码执行耗时,以及执行时间百分比,这篇文章主要介绍... 目录stopWatch 是org.springframework.util 包下的一个工具类，使用它
阅读更多...
Java进行文件格式校验的方案详解

Java进行文件格式校验的方案详解

《Java进行文件格式校验的方案详解》这篇文章主要为大家详细介绍了Java中进行文件格式校验的相关方案,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、背景异常现象原因排查用户的无心之过二、解决方案Magandroidic Number判断主流检测库对比Tika的使用区分zip
阅读更多...
Java实现时间与字符串互相转换详解

Java实现时间与字符串互相转换详解

《Java实现时间与字符串互相转换详解》这篇文章主要为大家详细介绍了Java中实现时间与字符串互相转换的相关方法,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、日期格式化为字符串（一）使用预定义格式（二）自定义格式二、字符串解析为日期（一）解析ISO格式字符串（二）解析自定义
阅读更多...
springboot security快速使用示例详解

springboot security快速使用示例详解

《springbootsecurity快速使用示例详解》：本文主要介绍springbootsecurity快速使用示例,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝... 目录创www.chinasem.cn建spring boot项目生成脚手架配置依赖接口示例代码项目结构启用s
阅读更多...
Python中随机休眠技术原理与应用详解

Python中随机休眠技术原理与应用详解

《Python中随机休眠技术原理与应用详解》在编程中,让程序暂停执行特定时间是常见需求,当需要引入不确定性时,随机休眠就成为关键技巧,下面我们就来看看Python中随机休眠技术的具体实现与应用吧... 目录引言一、实现原理与基础方法1.1 核心函数解析1.2 基础实现模板1.3 整数版实现二、典型应用场景2
阅读更多...
一文详解SpringBoot响应压缩功能的配置与优化

一文详解SpringBoot响应压缩功能的配置与优化

《一文详解SpringBoot响应压缩功能的配置与优化》SpringBoot的响应压缩功能基于智能协商机制,需同时满足很多条件,本文主要为大家详细介绍了SpringBoot响应压缩功能的配置与优化,需... 目录一、核心工作机制1.1 自动协商触发条件1.2 压缩处理流程二、配置方案详解2.1 基础YAML
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2