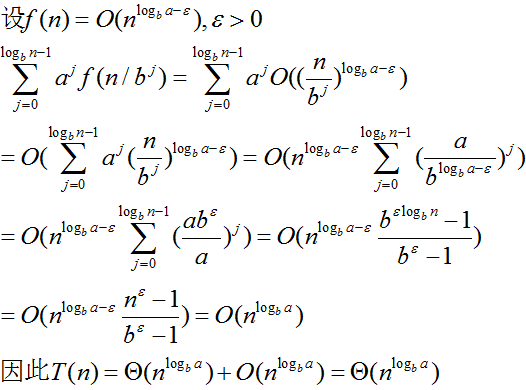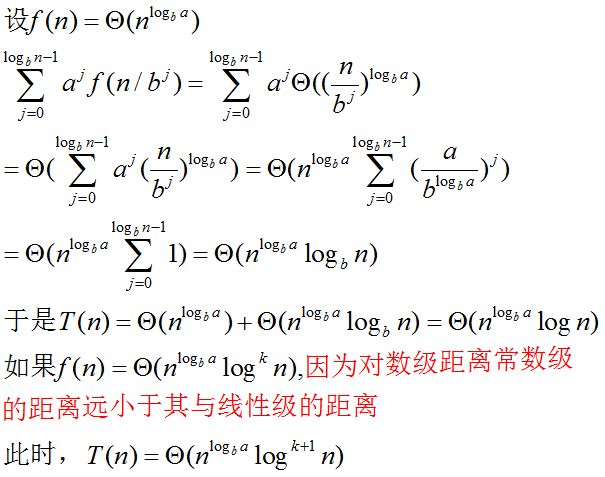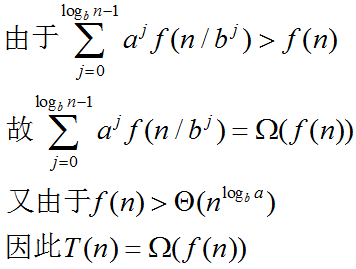本文主要是介绍分治、CDQ分治小结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
分治、CDQ分治小结 A Summary for Divide and Conquer
0. Anouncement
本文部分图片以及部分内容来自互联网,内容过多就不一一注明出处了,冒犯之处还请海涵。
Some of the pictures and the content of the text come from the Internet.
Due to plenty of the content, there will be no quotation. If offended, please try to forgive me.
Ⅰ. 分治
-
分治介绍
分而治之,将原问题不断划分为若干个子问题,直到子问题规模足够小可以直接解决
子问题间互相独立且与原问题形式相同,递归求解这些子问题,然后将各子问题的解合并得到原问题的解 -
一般步骤
- 划分 Divide
将原问题划分为若干个子问题,子问题间互相独立且与原问题形式相同 - 解决 Conquer
递归解决子问题(递归是彰显分治优势的工具,仅仅进行一次分治策略也许微不足道,
但递归划分到子问题规模足够小,子问题的解可用常数时间解决) - 合并 Merge
将各子问题的解合并得到原问题的解
- 划分 Divide
-
时间复杂度
- 直观估计
- 分治由以上三部分构成,整体的时间复杂度则由这三部分的时间复杂度之和构成。
- 由于递归,最终的子问题变得极为简单,以至于其时间复杂度在整个分治策略上的比重微乎其微
每次划分的子问题数是多少?每次划分与合并需要的时间是多少?
-
递归表达式与递归树
-
递归表达式
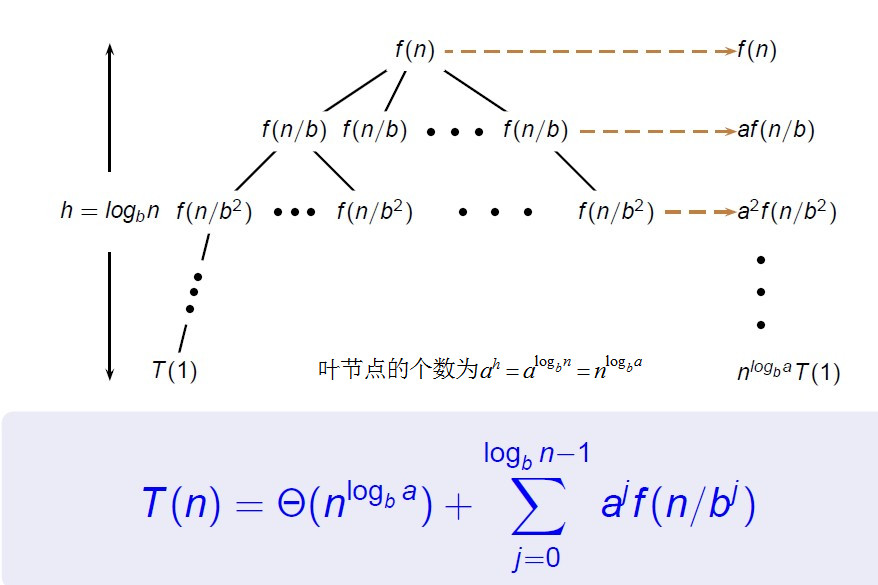
一般来说,分治将问题划分为 a 个同型子问题,子问题的规模是 n/b ,常数 a≥1, b>1
f(n) 是划分与合并 a 个大小为 n/b 的子问题的时间成本
f(n) 是一个渐进趋正的函数( ∃n0, 当n>n0, 有f(n)>0 )
递归表达式:T(n)=aT(n/b)+f(n) -
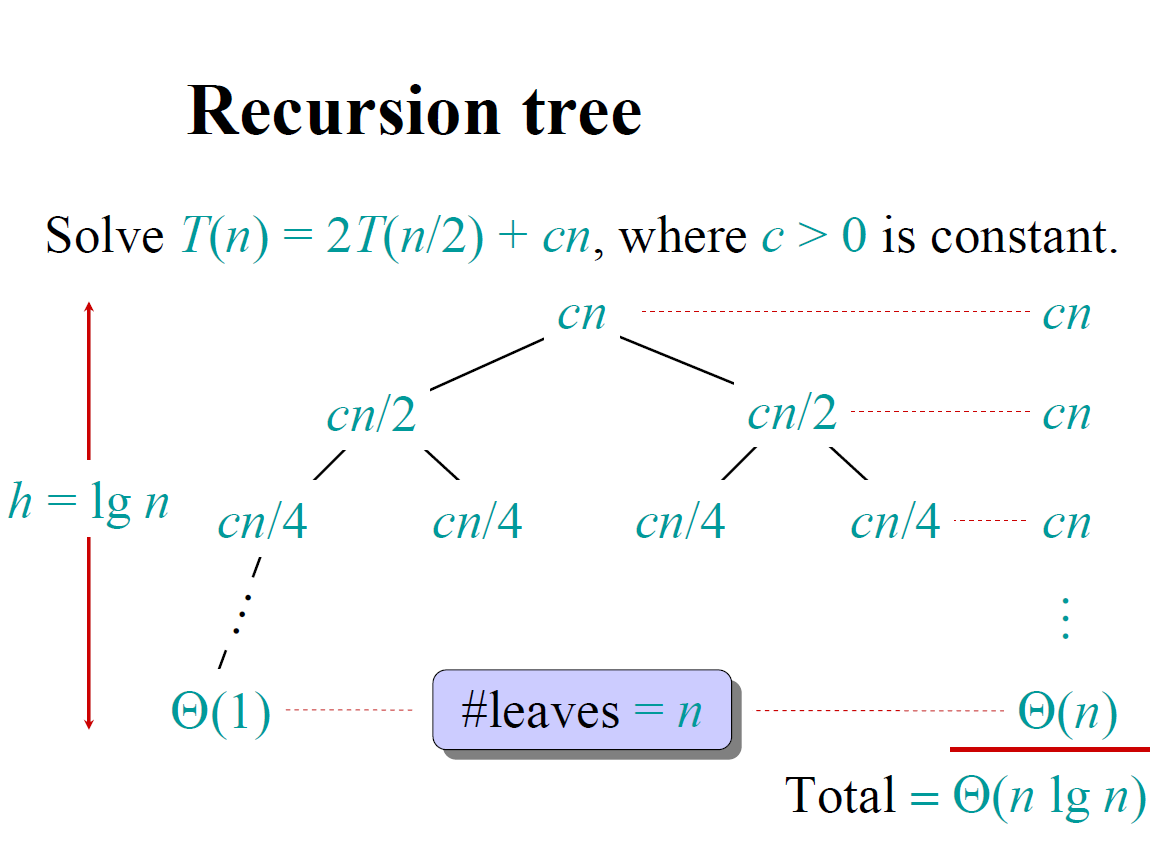
递归树
递归树是抽象的递归表达式具体化的图形表示,它给出的是一个算法递归执行的成本模型。
比如归并排序算法模型以输入规模为 n 开始,一层一层划分,直到输入规模变为 1 为止
-
-
替换法
替换法是先猜测某个界存在,再用数学归纳法证明正确性,通过解决表达式中的常数 c 来验证答案。
举例说明,用替换法证明 T(n)=T(n/4)+T(n/2)+n2 的解为 Θ(n2) ,即分别证明 T(n)=O(n2) 和 T(n)=Ω(n2)
-
∗ 主定理
-
主定理
递归表达式 T(n)=aT(n/b)+f(n)
T(n) 可能有如下的渐进界:
-
主定理的形象解释
-
T(n)=aT(n/b)+f(n) 的递归树
case 1 情况下,递归树的每层成本从根向下呈几何级数增长,成本在叶节点一层达到最高,即最后一次递归是整个过程中成本最高的一次,故其占主导地位。所以递归分治的总成本在渐进趋势上和叶子层的成本一样。
case 2 情况下,递归树每层的成本在渐进趋势上一样,即每层都是 nlogba 。由于有 logbn 层,因此总成本为每层的成本乘以 logbn 。
case 3 情况下,递归树每层成本呈几何级数递减,树根一层的成本占主导地位。因此,总成本就是树根层的成本。 -
主定理证明
-
case 1 由所有叶结点的代价决定
-
case 2 树的代价均匀地分布在各层上
-
case 3 由根结点的代价决定
特别说明:
f(n) 代表的是分治中的划分和合并的成本。由于 f(n) 的渐进增长趋势 >Θ(nlogba) ,
所以该分治的划分和合并的成本高于子问题的解决成本。而如果在这种情况要获得解,划分和合并的成本应该逐级下降
否则,划分和合并成本随着划分的推进将呈现发散趋势,这样总成本有可能不会收敛。那么这种分治就显得没有意义了
而如果划分与合并成本逐级下降,则意味着函数 f 满足 af(n/b)<=cf(n), c<1 。
因此,解为 T(n)=Θ(f(n))
-
-
- 直观估计
算法课就没去过几节,算导上主定理讲的也不是很详细,其实分析时间复杂度挺好玩的
转载整理上面的东西主要就是弥补之前书看不懂,课没去听吧,更多的还是结合做题以及具体算法理解吧
普通分治也不太用讲具体的东西,概念清楚,只要按照步骤来就很简单,并且有现成的例子来结合思考
两大杀器:快速幂、归并排序。举(照)一(猫)反(画)三(虎)即可
Ⅱ. CDQ分治
-
与普通分治的区别
普通分治中,每一个子问题只解决它本身(可以说是封闭的)
CDQ 分治中,对于划分出来的两个子问题,前一个子问题用来解决后一个子问题而不是它本身 -
适用的情况
在很多问题中(比如大多数数据结构题),经常需要处理一些动态问题
然而对动态问题的处理总是不如静态问题来的方便,于是就有了 CDQ 分治
但使用 CDQ 分治的前提是问题必须具有以下两个性质:- 修改操作对询问的贡献独立,修改操作互不影响效果
- 题目允许使用离线算法。
-
一般步骤
- 将整个操作序列分为两个长度相等的部分(分)
- 递归处理前一部分的子问题(治1)
- 计算前一部分的子问题中的修改操作对后一部分子问题的影响(治2)
- 递归处理后一部分子问题(治3)
特别说明:
在整个过程中,最核心的就是步骤3
此时前一部分子问题中的修改操作相对后一部分子问题来说是静态处理,因此可以更加方便地计算后一部分子问题
Ⅲ. CDQ分治的题目讲解
怎么学,强撸题吧,持续更新 ing
1. 静态问题
-
51nod 1376 最长递增子序列的数量
入门题の二维偏序,经典题目,点击查看题解 dp+树状数组详解 线段树 -
BZOJ 3262 陌上花开
入门题の三维偏序,经典题目,点击查看题解 -
HDU 4742 Pinball Game 3D
入门题の三维偏序, 求最长链以及数目,点击查看题解
CDQ 分治:
入门篇:l0nl1f3:简谈CDQ分治
1 概述
CDQ分治是啥?
会处理操作对于询问的影响吗?
对于一坨操作和询问,分成两半,单独处理左半边和处理左半边对于右半边的影响,就叫CDQ分治。
名字是为了纪念金牌选手陈丹琦
2 实现
将左右区间按一定规律排序后分开处理,递归到底时直接计算答案,对于一个区间,按照第二关键字split成两个区间,先处理左区间,之后因为整个区间是有序的,就可以根据左区间来推算右区间的答案,最后递归处理右区间即可。拿此题做比方,先把全区间按照x坐标排序,然后自左向右用前一半(按时间排序)的修改来更新后一半的查询,之后将整个区间按照时间分成两个部分,递归处理。归纳起来就是
1. 区间分成两半
2. 计算左区间对右区间的贡献
3. 撤销修改
4. 把操作分成两半
5. 递归下去做
CDQ分治 && HDU 5126
参考文献:从《Cash》谈一类分治算法的应用 — 陈丹琦
也因此简称CDQ分治。
个人理解CDQ分治和普通分治最大的区别为:
普通分治可以将问题拆成几个相互独立的子问题
CDQ分治将问题分成了两个部分:
- 相互独立的两个子问题
- 两个子问题之间的联系
因此,CDQ分治的算法流程也分为以下几步:
- 算法开始
- 取一个中间点mid, 将问题分为[L, mid] 和 [mid + 1, R]两个部分。分别处理两个子问题
- 处理[L, mid] 和 [mid + 1, R]之间的联系
举个例子:在二维坐标系中,有n个点,m个询问。对于每个询问(x, y),求点(x1, x2) ,x1<= x && y1 <= y 有多少个。
当然,这题用树状数组就直接能写了。但是我们在这里用CDQ分治来解决一下这个问题。
我们将n个点看做是n个更新,并和m个询问放在一起。定义一个结构体用vector存起来。
void sovle1(int l, int r, vector<Struct>vec1) {//在这里将vec1[l, r]按x从小到大排序int mid = (l + r) / 2;solve1(l, mid);solve1(mid + 1, r);//划分成相互独立的子问题//将vec1[l, mid]中的更新操作 和 vec1[mid + 1, r]中的询问操作,存到一个vec2中 solve2(l, r, vec2);//左半边的更新操作和右半边的询问操作之间有联系
}
void solve2(int l, int r, vector<Struct>vec2) {
//此时在solve2中已经不需要管x了。在vec2中所有的更新操作的x必然小于等于询问操作的x。//在这里将vec2[l, r]按y从小到大排序int mid = (l + r) / 2;sovle2(l, mid);solve2(mid + 1, r);//独立子问题//将vec2[l, mid]中的更新操作和vec2[mid + 1, r]中得询问操作存到一个vec3中solve3(l, r, vec3);//
}
void solve3(int l, int r, vector<Struct>vec3) {
//此时在solve3中,x和y都是已经排好序的。从前到后遍历该更新更新该询问询问就好。int cal = 0;for(Struct tmp: vec3) {if(tmp.type == Update) ++cal;else tmp.query_anser += cal;}
}
//这段代码其中有许多可以优化的地方,但是不要在意细节,主要是为了更加方便地理解算法
虽然解法不如树状数组,但是我们得看到题目扩展后的好处。
我们看到,当到solve2时,函数中的参数vec2已经不用再管他的x了(请务必深刻理解为什么不用再管了)。
这样的好处在哪里?没错,降维!
假如我们要处理的不是二维,而是三维四维依旧可以这么处理,每一个维度只不过加了O(log)的复杂度而已。
如果是随时可以更新查询的操作,只不过也只是把时间当成一个维度而已。(光是这一点就已经牛逼哄哄够解决大部分题目了。)
然后就是下面这道题,三维且可随时更新查询:
HDU 5126 starts: 传送门
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <vector>
#include <cstdlib>
using namespace std;
#define FOR(i,l,r) for(int i=(l); i<=(r); ++i)
#define REP(i,r) for(int i=0; i<(r); ++i)
#define DWN(i,r,l) for(int i=(r);i>=(l);--i)
#define pb push_back
typedef long long ll;
typedef pair<int, int>pii;
const int N = 5e4 + 100;
int que[N << 1];
int ans[N];
int z_num;
int node[N << 1];
struct Query {int x, y, z, kind, id;Query() {}Query(int _x, int _y, int _z, int _kind, int _id) : x(_x), y(_y), z(_z), kind(_kind), id(_id) {}
}queries[N << 3], queries_x[N<<3], queries_y[N << 3];
bool cmpx(Query a, Query b) {return a.x < b.x || (a.x == b.x && a.kind < b.kind);
}
bool cmpy(Query a, Query b) {return a.y < b.y || (a.y == b.y && a.kind < b.kind);
}
inline int lowbit(int x) {return x&-x;}
void update(int pos, int value) {while(pos <= z_num) {node[pos] += value;pos += lowbit(pos);}
}
int query(int pos) {int ret = 0;while(pos) {ret += node[pos];pos -= lowbit(pos);}return ret;
}
void solve3(int l, int r) {//只剩下二维y和z,直接就是二维的更新查询题目,树状数组解决就好了if(l >= r) return;FOR(i, l, r)if(queries_y[i].kind == 0) update(queries_y[i].z, 1);else if(queries_y[i].kind == 1) ans[ queries_y[i].id ] -= query(queries_y[i].z);else if(queries_y[i].kind == 2) ans[ queries_y[i].id ] += query(queries_y[i].z);FOR(i, l, r)if(queries_y[i].kind == 0) update(queries_y[i].z, -1);
}
void solve2(int l, int r) {//把x这一维度消除if(l >= r) return;int mid = (l+r)>>1;solve2(l, mid);solve2(mid + 1, r);int num = 0;FOR(i, l, mid) if(queries_x[i].kind == 0) queries_y[num++] = queries_x[i];FOR(i, mid+1, r) if(queries_x[i].kind) queries_y[num++] = queries_x[i];sort(queries_y, queries_y + num, cmpy);solve3(0, num - 1);
}
void solve1(int l, int r) {//已经默认时间从小到大排序了,把时间这一维度消除if(l >= r) return;int mid = (l+r)>>1;solve1(l, mid);solve1(mid + 1, r);int num = 0;FOR(i, l, mid) if(queries[i].kind == 0) queries_x[num++] = queries[i];FOR(i, mid + 1, r) if(queries[i].kind) queries_x[num++] = queries[i];sort(queries_x, queries_x + num, cmpx);//对x从小到大排序solve2(0, num - 1);
}
int main() {int casnum, n;int x1, x2, y1, y2, z1, z2, kind;cin >> casnum;while(casnum--) {memset(ans, -1, sizeof(ans));cin >> n;int id = 0;z_num = 0;REP(i, n) {scanf("%d", &kind);if(kind == 1) {scanf("%d%d%d", &x1, &y1, &z1);queries[id++] = Query(x1, y1, z1, 0, i);que[z_num++] = z1;} else {ans[i] = 0;scanf("%d%d%d%d%d%d", &x1, &y1, &z1, &x2, &y2, &z2);queries[id++] = Query(x2 , y2 , z2 , 2, i);queries[id++] = Query(x2 , y2 , z1 - 1, 1, i);queries[id++] = Query(x2 , y1 - 1, z2 , 1, i);queries[id++] = Query(x1 - 1, y2 , z2 , 1, i);queries[id++] = Query(x2 , y1 - 1, z1 - 1, 2, i);queries[id++] = Query(x1 - 1, y2 , z1 - 1, 2, i);queries[id++] = Query(x1 - 1, y1 - 1, z2 , 2, i);queries[id++] = Query(x1 - 1, y1 - 1, z1 - 1, 1, i);que[z_num++] = z2;que[z_num++] = z1 - 1;}}sort(que, que + z_num);z_num = unique(que, que + z_num) - que;REP(i, id) queries[i].z = lower_bound(que, que + z_num, queries[i].z) - que + 1;solve1(0, id - 1);REP(i, n)if(ans[i] != -1)printf("%d\n", ans[i]);}return 0;
}
这篇关于分治、CDQ分治小结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!