基于DTW距离测度的Kmeans时间序列聚类算法

本文主要是介绍基于DTW距离测度的Kmeans时间序列聚类算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原理介绍

1. DTW距离：

• 当两个时间序列不等长时，传统的欧氏距离难以度量它们的相似性。DTW通过调节时间点之间的对应关系，能够寻找两个任意长时间序列中数据之间的最佳匹配路径。
• DTW算法的基本思想是通过将时间序列进行弯曲、拉伸等变换，找到它们之间的最佳匹配路径，从而得到它们之间的相似度。在DTW算法中，距离越小表示两个时间序列越相似。
• DTW对噪声有很强的鲁棒性，适用于语音识别、手写体识别、生物信息学、金融时间序列分析等领域。

1. K-means聚类算法：

• K-means算法基于迭代优化，旨在将数据点划分为k个簇，使得每个数据点都属于最近的簇，并且簇的中心是所有数据点的平均值。
• K-means算法的初始化阶段随机选择k个数据点作为初始簇中心，然后通过迭代将数据点分配给最近的簇中心，并更新簇中心点，直到达到收敛条件或预定的迭代次数。

1. 结合DTW和K-means：

• 在时间序列聚类中，传统的K-means算法使用欧氏距离作为相似度度量，但这对不等长的时间序列不适用。因此，基于DTW距离的K-means算法使用DTW距离取代欧氏距离，使得算法能够处理不等长的时间序列。
• 该算法首先计算所有时间序列对之间的DTW距离，然后使用这些距离作为输入来执行K-means聚类。

基于DTW（动态时间规整）距离的K-means时间序列聚类算法与传统的K-means算法相比，主要在以下几个方面有所不同：

1. 距离度量：

   • 传统K-means算法使用欧氏距离作为相似度或距离度量，它适用于等长数据的聚类。然而，在处理时间序列数据时，尤其是长度不等的时间序列，欧氏距离可能不再适用。
   • 基于DTW距离的K-means算法使用DTW距离作为度量，DTW是一种能够处理不等长序列的相似度度量方法。它通过动态规划找到两个时间序列之间的最佳对齐方式，并计算对齐后的序列之间的距离。这使得算法能够处理不等长的时间序列数据。

2. 聚类结果：

   • 传统K-means算法通过迭代将数据点分配给最近的簇中心，并更新簇中心，直到达到收敛条件或预定的迭代次数。由于使用欧氏距离，它通常适用于空间中的聚类问题。
   • 基于DTW距离的K-means算法则通过计算时间序列之间的DTW距离，将数据序列分配到最近的簇中，并更新簇中心为簇内序列的某种代表（可能是平均值或最接近平均值的实际序列）。这使得算法能够发现时间序列数据中的模式和结构。

3. 适用场景：

   • 传统K-means算法适用于空间数据的聚类，如二维或三维空间中的点数据。它在图像处理、机器学习等领域有广泛应用。
   • 基于DTW距离的K-means算法特别适用于时间序列数据的聚类。它可以用于分析具有时间顺序的数据，如股票价格、气象数据、生物信号等。在这些领域中，时间序列数据往往具有不等长的特性，因此基于DTW距离的K-means算法更具优势。

4. 算法复杂度：

   • 传统K-means算法的时间复杂度通常为O(nkt)，其中n是数据点的数量，k是簇的数量，t是迭代次数。
   • 基于DTW距离的K-means算法的时间复杂度可能会更高，因为计算DTW距离本身就是一个相对耗时的过程。然而，对于处理时间序列数据来说，这种复杂度是可以接受的，并且算法通常能够在合理的时间内完成聚类任务。

综上所述，基于DTW距离的K-means时间序列聚类算法在距离度量、聚类结果、适用场景和算法复杂度等方面与传统K-means算法有所不同。它特别适用于处理不等长的时间序列数据，并能够在这些数据中发现有用的模式和结构。

部分代码：

clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
%% ============================导入数据=============================
data = xlsread('序列数据.xlsx');
X = data;                        % 特征序列
%% ============================kmeans聚类===========================
K = 3;  
[idx,C] = mykmeans(X,K,[],[],[],'Dtw','sample');   % 'plus'\'sample'
%% =============================聚类结果可视化=======================
Cor = linspecer(K);
figure()
name = [];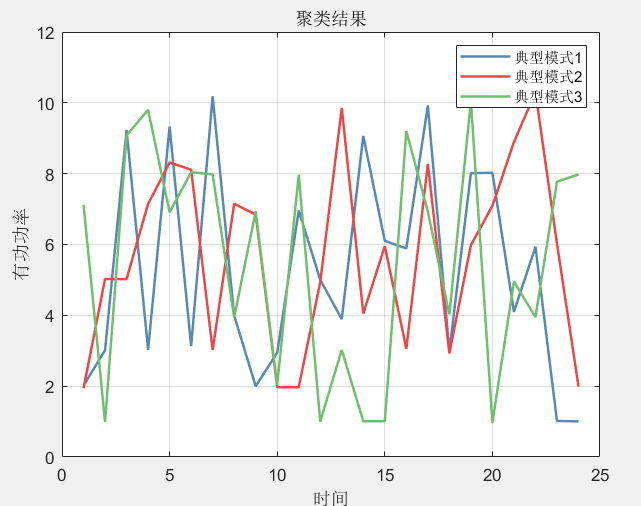

这篇关于基于DTW距离测度的Kmeans时间序列聚类算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---