本文主要是介绍Python数据分析案例43——Fama-French回归模型资产定价(三因子/五因子),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
案例背景
最近看到要做三因子模型的同学还挺多的,就是所谓的Fama-French回归模型,也就是CAMP资本资产定价模型的升级版,然后后面还升级为了五因子模型。
看起来眼花缭乱,其实抛开金融资产定价的背景,从机器学习角度来看,就是多元线性回归.......很low也很简单。
数据也很简单,以日度数据为例,y就是一个资产的日度收益率,例如一只股票的每天的收益率。X就是日度的五个因子数据,
- mkt_rf [市场风险因子](rf是[无风险利率])
- smb [规模风险因子]
- hml [账面市值比风险因子]
- rmw[盈利能力因子] 更高盈利能力的公司通常预示更健康的财务状况和更低的风险。
- cma[投资风格因子]
为什么用的是线性回归模型,因为三因子五因子提出来的年代还没机器学习的思路,而且线性回归的解释能力强,能更好的表现不同因子的作用。虽然机器学习也能做这个数据集,但是其黑箱的过程不是很好解释。
数据
股票数据很好获取的,网上到处都有,本文使用akshare的接口来获取,后面代码会演示。
五因子的数据长这个样子:
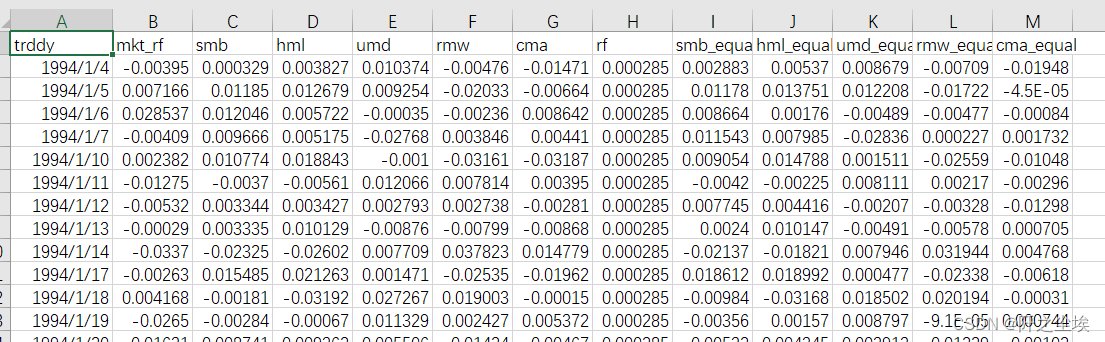
很全,从1994年到2024年4月都有,不仅有日度的五因子,还有很多其他的等价因子等。需要本次演示的全部代码和数据的同学可以参考:五因子数据。
股票选择:
选什么股票来演示这个案例呢,我懒得自己去找了,让kimi帮我找了几个2024年具有较好的价值的股票代码: (本案例仅仅只是代码演示,不构成任何投资意见)
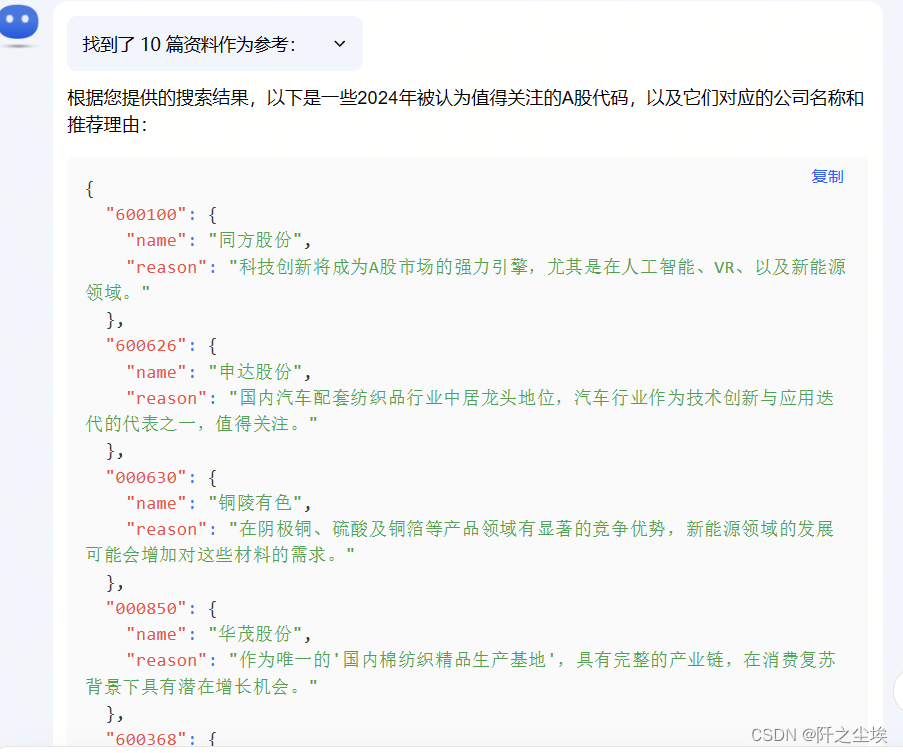
OK他提供了几个股票的编号和名称就行,下面开始写代码。
代码实现
导入数据分析常用的包:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
plt.rcParams ['font.sans-serif'] ='SimHei' #显示中文
plt.rcParams ['axes.unicode_minus']=False #显示负号股票代码:,然后设定时间,我设定为23年的4月到24年的3月底
code_name={"600100": "同方股份","600626": "申达股份","000630": "铜陵有色","000850": "华茂股份","600368": "五洲交通","603766": "隆鑫通用","600105": "永鼎股份","600603": "广汇物流","002344": "海宁皮城","000407": "胜利股份","000883": "湖北能源"}
code_list=list(code_name.keys())
start_date='2023-04-01' ; end_date='2024-03-31'下面获取这些股票的交易数据,
首先自定义一个获取股票交易日K的数据的代码:
import akshare as ak
# 定义获取A股历史交易数据的函数
def get_stock_data(stock_code, start_date, end_date):""":param stock_code: 股票代码,如 '000001':param start_date: 开始日期,格式为 'YYYYMMDD':param end_date: 结束日期,格式为 'YYYYMMDD':return: 指定时间段内的股票交易数据(DataFrame)"""# 使用 AkShare 的 stock_zh_a_hist 接口获取数据stock_df = ak.stock_zh_a_hist(symbol=stock_code, period="daily", start_date=start_date.replace('-',''), end_date=end_date.replace('-',''), adjust="qfq")stock_df['收益率'] = stock_df['收盘'].pct_change() return stock_df.dropna()创建一个字典来存放获取的结果,然后遍历所有的股票代码,一个个获取,存入这个字典的值。
return_dict={}
#创建一个 ExcelWriter 对象
#writer = pd.ExcelWriter('股票数据.xlsx', engine='xlsxwriter')
for code in code_list:try:return_dict[code]=get_stock_data(stock_code=code,start_date=start_date,end_date=end_date)[['日期','收盘','收益率']].set_index('日期')#get_stock_data(stock_code=code,start_date='20230201',end_date='20240201').to_excel(writer, sheet_name=code)except:pass
#writer.save()
#writer.close()return_dict这个字典的键就是股票代码,值就是对应的股票交易数据的df数据框。
(ps:注释掉的地方是可以进行运行了,会把所有股票的交易数据存入一个excel表里面保存下来,需要的同学可以运行)
取出其中一个看看:
return_dict['600368'].head()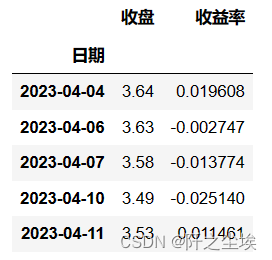
读取因子的数据,我筛选了时间和变量,保证读取进来的就是2023年4月到2024年3月底的数据。变量就是5个因子,别的变量就没要。
#读取因子数据
three_factors=pd.read_csv('fivefactor_daily.csv')[['trddy','mkt_rf','smb','hml','rmw','cma']].rename(columns={'trddy':'日期'}).set_index('日期')
three_factors=three_factors.loc['2023-04-01':'2024-03-31',:]
three_factors.index=pd.to_datetime(three_factors.index)
three_factors.head(3)展示的前三行:
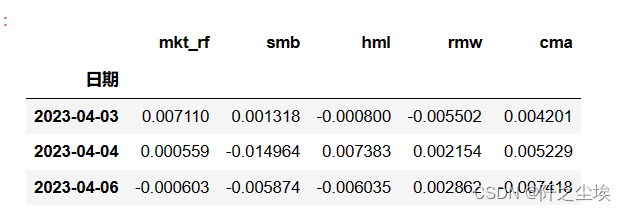
再简单介绍一下这些变量的含义:
- trddy [交易日期]
- mkt_rf [市场风险因子]
- smb [规模风险因子]
- hml [账面市值比风险因子]
- rf [无风险利率]
- rmw[盈利能力因子] 更高盈利能力的公司通常预示更健康的财务状况和更低的风险。
- cma[投资风格因子]
需要这个数据的同学看前面。
自定义一些函数,学过金融的背景的同学应该都知道是什么作用的,主要都是测量一个资产的表现,衡量其收益的风险的。
def sum_return_ratio(price_list):'''实际总收益率'''price_list=price_list.to_numpy()return (price_list[-1]-price_list[0])/price_list[0]
def MaxDrawdown(price_list):'''最大回撤率'''i = np.argmax((np.maximum.accumulate(price_list) - price_list) / np.maximum.accumulate(price_list)) # 结束位置if i == 0:return 0j = np.argmax(price_list[:i]) # 开始位置return (price_list[j] - price_list[i]) / (price_list[j])
def sharpe_ratio(price_list,rf=0.000041):'''夏普比率'''#公式 夏普率 = (回报率均值 - 无风险率) / 回报率的标准差# pct_change()是pandas里面的自带的计算每日增长率的函数daily_return = price_list.pct_change()return daily_return.mean()-rf/ daily_return.std()
def Information_Ratio(price_list,rf=0.000041):'''信息比率'''chaoer=sum_return_ratio(price_list)-((1+rf)**365-1)return chaoer/np.std(price_list.pct_change()-rf)三因子模型

不知道三因子是啥看看就行,反正就是线性回归......Python里面就用statsmodel就行。
自定义函数,可以输入股票的数据,然后返回这个股票的 '阿尔法','市场风险因子MKT','市值因子SMB','账面市值因子HML','实际总收益率','最大回测率':'夏普比率':,'信息比率','股票代码'。
如果参数mode输入的是‘五因子’的模型,则会多返回:盈利能力因子RMW','投资风格因子CMA,这两个数值。
def deal(code='',mode='三因子'): day_return = return_dict[code]#['收益率']day_return.index=pd.to_datetime(day_return.index)实际总收益率=sum_return_ratio(day_return['收盘'])最大回测率=MaxDrawdown(day_return['收盘'])夏普比率=sharpe_ratio(day_return['收盘'])信息比率=Information_Ratio(day_return['收盘'])zgpa_threefactor = pd.merge(three_factors, day_return,left_index=True, right_index=True) if mode=='五因子':result = sm.OLS(zgpa_threefactor['收益率'], sm.add_constant(zgpa_threefactor.loc[:,['mkt_rf','smb','hml','rmw','cma']])).fit()betas=result.paramsreturn pd.DataFrame({'阿尔法':betas[0],'市场风险因子MKT':betas[1],'市值因子SMB':betas[2],'账面市值因子HML':betas[3],'盈利能力因子RMW':betas[4],'投资风格因子CMA':betas[5],'实际总收益率':实际总收益率,'最大回测率':最大回测率,'夏普比率':夏普比率,'信息比率':信息比率,'股票代码':code},index=[0])else:#zgpa_threefactor = pd.merge(three_factors, day_return,left_index=True, right_index=True)result = sm.OLS(zgpa_threefactor['收益率'], sm.add_constant(zgpa_threefactor.loc[:,['mkt_rf','smb','hml']])).fit()betas=result.paramsreturn pd.DataFrame({'阿尔法':betas[0],'市场风险因子MKT':betas[1],'市值因子SMB':betas[2],'账面市值因子HML':betas[3],'实际总收益率':实际总收益率,'最大回测率':最大回测率,'夏普比率':夏普比率,'信息比率':信息比率,'股票代码':code},index=[0])然后循环计算所有股票的这些数值,合并到一起,很方便:
df_results=pd.DataFrame()
for code,df_one in return_dict.items():result=deal(code=code) ; result['股票名称']=code_name[code]df_results=pd.concat([df_results,result],axis=0,ignore_index=True)选出阿尔法前十的股票 来分析画图
整理一下,我们按照阿尔法的大小排序,查看结果:
df_results=df_results[['股票代码', '股票名称','阿尔法', '市场风险因子MKT', '市值因子SMB', '账面市值因子HML', '实际总收益率', '最大回测率', '夏普比率', '信息比率']].sort_values(by='阿尔法',ascending=False)
df_results
看数据不够直观,我们画个图看看:
plt.figure(figsize=(10, 8),dpi=128)# 创建多子图布局
for i, column in enumerate(['阿尔法', '市场风险因子MKT', '市值因子SMB', '账面市值因子HML', '实际总收益率', '最大回测率', '夏普比率', '信息比率'], 1):plt.subplot(4, 2, i)plt.bar(df_results.head(10)['股票名称'], df_results.head(10)[column], color='skyblue')plt.title(column)plt.xticks(rotation=45) # 旋转标签,避免重叠# 调整布局
plt.tight_layout()
plt.show()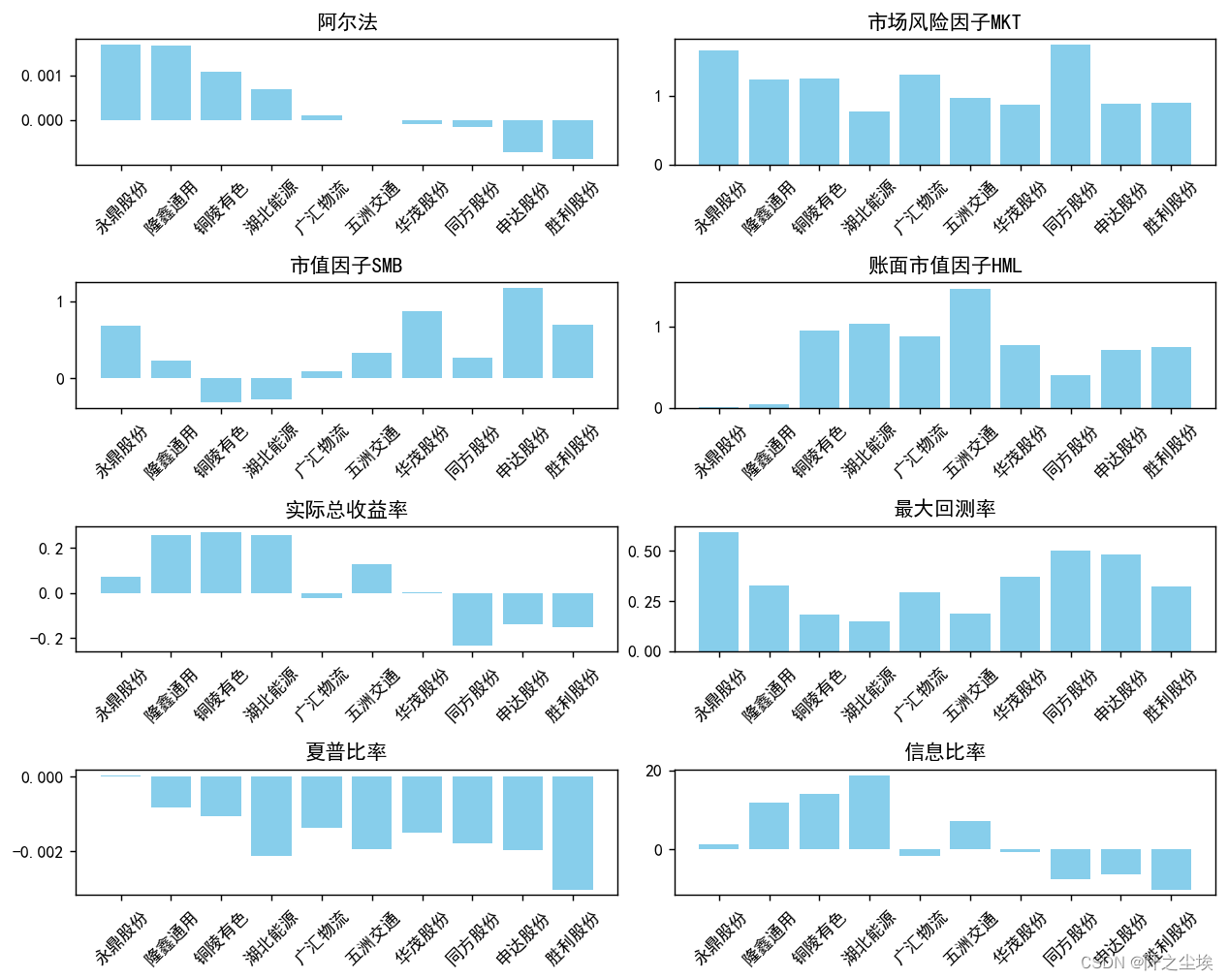
可以从图中清楚的看到哪些股票的哪些指标是领先的。分析我就不多写了,写了可能也没那么通俗易懂,还是让我们的gpt同学来写:
‘’要分析这些股票的投资价值和风险,我们可以根据你提供的数据来进行一些基本的评估。数据中包括了阿尔法值(α)、市场风险因子(MKT)、市值因子(SMB)、账面市值因子(HML)、实际总收益率、最大回撤率、夏普比率以及信息比率。这些指标各自反映了股票的不同风险和收益特征:
-
阿尔法(α):表示股票相对于基准的超额回报。正值表示超出市场预期的回报,更高的正值通常被视为更好。
-
市场风险因子(MKT):系数高意味着股票与市场整体更同步,风险和市场相近。
-
市值因子(SMB):反映小市值股票与大市值股票的表现差异,正值表明倾向于小市值股票特性。
-
账面市值因子(HML):反映高账面市值比与低账面市值比股票的表现差异,正值表明倾向于价值股特性。
-
实际总收益率:这是投资者最终关心的实际收益率。
-
最大回撤率:表示股票价格在观察期内的最大下跌幅度,较小的数值表示下跌风险较低。
-
夏普比率:衡量调整风险后的收益,数值越高表示单位风险带来的额外回报越多。
-
信息比率:衡量管理绩效的一种指标,反映了投资组合超过基准回报的能力,数值越高表明超越基准的能力越强。
分析建议:
我们可以从以上各指标来分析哪些股票看起来更有投资价值:
-
阿尔法值较高:永鼎股份、隆鑫通用、铜陵有色,这些股票在调整市场因素后显示了较好的超额回报。
-
最大回撤率较低:湖北能源、胜利股份、同方股份等有较低的最大回撤率,这表明在最坏的情况下它们的价值减少较少,相对稳定。
-
夏普比率和信息比率:隆鑫通用和铜陵有色的信息比率较高,虽然夏普比率为负,这可能表明在评估期内它们面临一定的波动性或负面风险。夏普比率为负通常是一个警示信号,需要结合其他因素综合考虑。
综合考虑以上指标,铜陵有色和隆鑫通用在信息比率高的情况下,表现出了超越市场的潜力,尽管它们的夏普比率为负。永鼎股份虽然信息比率较低,但阿尔法值较高且夏普比率为正,显示了其稳定的超额收益能力。
在投资决策前,还应考虑其他因素如行业状况、公司基本面、市场整体环境等,这里的分析仅基于提供的数据。此外,负夏普比率需要进一步的调查和理解,可能涉及较高的风险。‘’
储存这个表:,方便复制到论文或者作业里面去。
### 储存结果
df_results.to_csv('三因子结果.csv',index=False)五因子模型

和三因子差不多,就多了两个其他的变量,代码上前面都自定义好了,这里就很简单:
先循环遍历去回归
df_results=pd.DataFrame()
for code,df_one in return_dict.items():result=deal(code=code,mode='五因子') ; result['股票名称']=code_name[code]df_results=pd.concat([df_results,result],axis=0,ignore_index=True)然后整理结果,按照阿尔法从大到小排序,查看:
df_results=df_results[['股票代码', '股票名称','阿尔法', '市场风险因子MKT', '市值因子SMB', '账面市值因子HML', '盈利能力因子RMW','投资风格因子CMA','实际总收益率', '最大回测率', '夏普比率', '信息比率']].sort_values(by='阿尔法',ascending=False)
df_results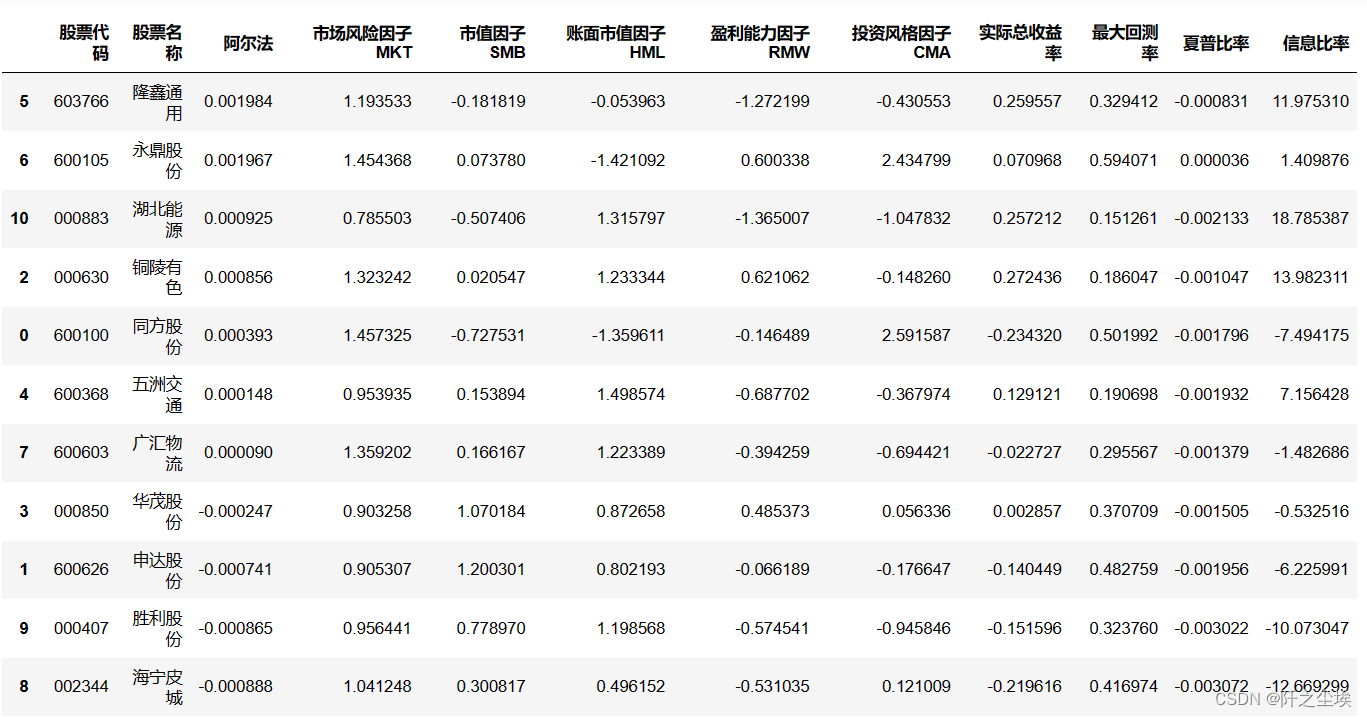
看数值不直观,画个图:
plt.figure(figsize=(10,10),dpi=128)# 创建多子图布局
for i, column in enumerate(['阿尔法', '市场风险因子MKT', '市值因子SMB', '账面市值因子HML', '盈利能力因子RMW','投资风格因子CMA', '实际总收益率', '最大回测率', '夏普比率', '信息比率'], 1):plt.subplot(5, 2, i)plt.bar(df_results.head(10)['股票名称'], df_results.head(10)[column], color='skyblue')plt.title(column)plt.xticks(rotation=45) # 旋转标签,避免重叠plt.tight_layout()
plt.show()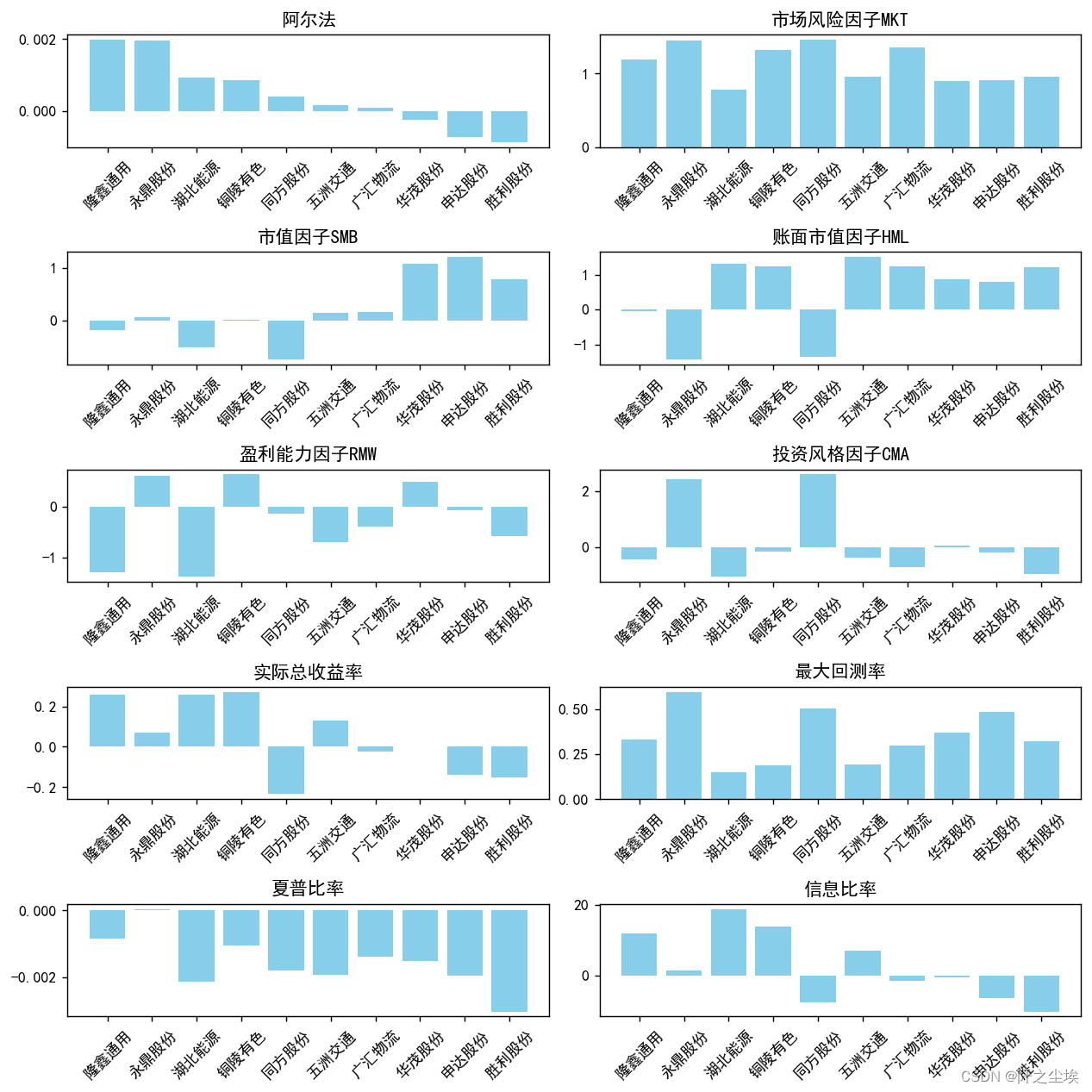
gpt的分析:
“
关键指标分析
-
阿尔法(α):代表超额回报。较高的阿尔法值意味着股票在考虑了相关风险因子后,表现超出市场平均水平。
-
市场风险因子(MKT):衡量股票与市场整体波动的相关性。高值表明股票价格波动与市场紧密相关。
-
市值因子(SMB)和账面市值因子(HML):这两个因子帮助评估股票在大小和价值方面的表现倾向。
-
盈利能力因子(RMW)和投资风格因子(CMA):RMW高表明公司盈利能力强,CMA高则说明公司投资保守。
-
实际总收益率、最大回测率、夏普比率和信息比率:这些都是评估投资回报和风险的重要指标。
根据数据分析
-
**隆鑫通用(603766)和永鼎股份(600105)**的阿尔法值较高,但隆鑫通用的盈利能力因子(RMW)为负且较大,可能表明其盈利能力不稳定。永鼎股份的投资风格因子(CMA)非常高,暗示其投资策略较为保守。
-
**湖北能源(000883)和铜陵有色(000630)**同样显示出较好的阿尔法值,且铜陵有色的盈利能力较好,但湖北能源的盈利能力和投资风格因子均为负,这可能指示了较高的风险。
-
同方股份(600100)、申达股份(600626)、**胜利股份(000407)和海宁皮城(002344)**的阿尔法值为负,且信息比率也为负,这表明它们的表现可能不理想。
投资建议
-
在这组数据中,铜陵有色可能是较为有吸引力的投资选择,因为它在盈利能力和市场相关性上表现较好,且有积极的超额回报。
-
对于永鼎股份,尽管阿尔法值高,但需要进一步考察其极高的投资风格因子对未来表现的影响。
-
对于显示出负阿尔法值和信息比率的股票,建议谨慎考虑,可能需要更多的分析来确定其表现不佳的具体原因。
投资决策应综合考虑这些指标以及其他外部因素,如行业趋势、公司基本面分析、宏观经济条件等。在做出投资选择前,进行全面的风险评估和市场研究是非常重要的。
”
### 储存结果
df_results.to_csv('五因子结果.csv',index=False)创作不易,看官觉得写得还不错的话点个关注和赞吧,本人会持续更新python数据分析领域的代码文章~(需要定制类似的代码可私信)
(本案例仅共学习和参考,不构成任何投资意见)
这篇关于Python数据分析案例43——Fama-French回归模型资产定价(三因子/五因子)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




