本文主要是介绍近似消息传递算法(AMP)单测量模型(SMV),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、算法解决问题
很多人致力于解决SLM模型的求逆问题,即知道观测值和测量矩阵(字典之类的),要求未知变量的值。SLM又叫做标准线性模型,后续又在此基础上进行升级变为广义线性模型。即SLM是y=Ax+e,这里是线性关系,而到广义里可能就不单单只是Ax这个线性关系,可能是一个非线性函数y=F(x),此时就适合进一步的广义近似消息传递GAMP。并且在压缩感知CS出现后,又有很多人的兴趣转向与稀疏信号重构的问题。到底怎么才能解这个方程又快又准呢。大多数时候这二者不可兼得,我们要取其中之一。比如经典的贪婪算法或者叫追踪算法的衍生类,它们扮演着一步步找最优原子(最相关的原子)来扩展它的支撑集,直到迭代终止,这个过程涉及矩阵求逆,在测量矩阵维度高的情况下复杂度及其高。后续又有凸优化类的算法,由于本人涉猎不多,词穷。后面还有稀疏贝叶斯类算法(像什么伯努利高斯(Spike and slab)、稀疏贝叶斯学习(SBL))都是用来解决稀疏信号重构的问题。而稀疏信号重构就涉及通信领域的一个大规模机器通信或者叫IOT,而这个稀疏性又可以表示在OTFS系统下的信道物理特性。因此算法可以经过改进而应用到信道估计和活跃用户检测。或者是符号检测及活跃用户检测上。
2、算法由来
[1]Donoho, David L., Arian Maleki, and Andrea Montanari. "Message-passing algorithms for compressed sensing." Proceedings of the National Academy of Sciences 106.45 (2009): 18914-18919.
[2]Donoho, David L., Arian Maleki, and Andrea Montanari. "How to design message passing algorithms for compressed sensing." preprint (2011).
由Donoho等人在[1,2]中引入的近似消息传递(AMP)算法, AMP 是一个基于消息传递的框架,为解决压缩感知背景下的基追踪或基追踪去噪问题而开发。AMP 也可以被视为迭代阈值算法类的一个实例。然而,AMP 与此类其他算法的区别在于,它具有显着更好的稀疏性欠采样权衡。
3、算法
[3]Andersen, Michael Riis. "Sparse inference using approximate message passing." Technical University of Denmark, Department of Applied Mathematics and Computing (2014).
考虑线性方程组 ,其中
、
和
是真解。假设 A 的列已缩放至单位“2-范数”。给定问题的欠采样率 δ 将定义为 δ = m/n,k 表示真实解中非零元素的数量,稀疏度将定义为 ρ = k/m 。对于基追踪问题,AMP 的简单更新方程由下式给出
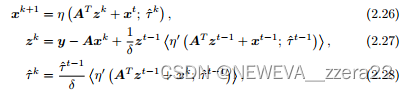
以上算法是无噪声版本的AMP,下式是我们常用的有噪声版本。通常噪声服从零均值固定方差的高斯或者复高斯分布,即高斯白噪声。

短短的三行公式,却有着很大魅力。其中 λ 是正则化参数。通过比较 BP 和 BPDN 的更新方程,可以看出,当 λ = 0 时,两种算法是相同的,因此我们只关注后者而不失一般性。
我读了一篇国外的硕士论文,eta函数是这麽推到的(来源于消息传递因子图,当然我也是这个方向的)当然这个图不清晰,我把论文[3]标题附在上方
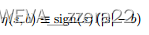
当然eta的导数文中也有推到,需要的自己去查看即可
其实就是一个倒门函数,在特定区间为0,其他为1
4、算法代码(来源Github)
当然这个稀疏值个数也不是必须的,tau初始化为1也是可以正常运行的。
function xest = amp(y,sparsity,A,niter)[M,N]=size(A);
tau = sqrt(2*log10(M/sparsity)); % needs to be tuned in case of unknown prior sparsity level%% Approximate Message Passing for basis selection
% Initializing
xest = zeros(N,1);
z = y;
eta = @(x,beta) (x./abs(x)).*(abs(x)-beta).*(abs(x)-beta > 0); % denoising function
for iter=1:nitersigma = norm(z,2)/sqrt(M);xest = eta(xest + A'*z, tau*sigma);tmp = sum(abs(xest) > 0);z = y - A*xest + (tmp/M)*z;
end%[abs(xest) abs(x)]
end5、稀疏信号重构demo
做一个测试demo,测量数为稀疏信号维度的一半,稀疏度13/128。噪声估计也是很小的。当然如果想设计信噪比下的恢复效果。可以根据信噪比公式去设置。就是那个dB转换公式,将其中一个已知,来求解另一个。比如dB=20,此时你生成的观测和稀疏向量是暂时知道的,通过他俩计算信号功率,然后得到噪声功率。当然想了解的人可以去关注我一个师兄的公众号MessagePassing或者是搜一搜。
信噪比SNR的两种计算方法
clc;
clear all;
N = 128; % length of vector to be recovered
M = 64; % number of measurement
A = (1/sqrt(2))*(normrnd(0,1/sqrt(M),M,N) + 1i*normrnd(0,1/sqrt(M),M,N)); % Sensing matrix construction for theroetical bound
x = zeros(N,1); % Initializing sparse vector to be recovered
k = 13; % Sparsity level
uset = randperm(N,k);
x(uset) = rand(k,1) + 1i*rand(k,1); % Sparse vector initialized
noise = sqrt(1/2)*(normrnd(0,1,M,1) + 1i*normrnd(0,1,M,1)); % zero mean, unit covariance complex noise vector
var = 1e-11;
noise = sqrt(var)*noise;
y = A*x + noise; % create measurement
niter = 30; % number of iteration
%% Approximate Message Passing for basis selection
xest = amp(y,k,phi,niter);
plot(abs(x),'r-o');hold on;
plot(abs(xest),'b+-');
legend('xreal','xest');
title('recover complex signal')
nmse=norm(xest-x).^2/(norm(x).^2);
disp(nmse)
%[abs(xest) abs(x)]
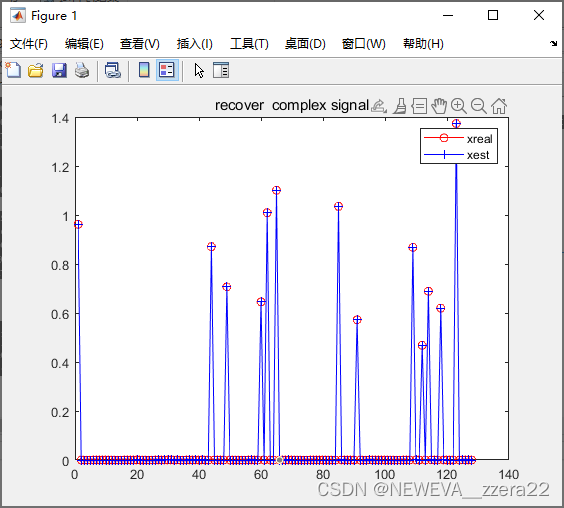
效果图及NMSE如下,当然想去与OMP做对比的也可以。OMP算法要知道稀疏度或者是一些带噪声根据阈值来判断的变体算法也不是很好,很容易找错。当然后续我也会更新一些其他的算法及代码
8.3788e-11
6、根据论文复现的AMP0代码

function [x_est] = AMP_Lplace(y,A,maxiter)
%%根据论文写的AMP0算法,效果没有之前的GitHub上的好
[M,N]=size(A);
%% Approximate Message Passing for Laplace Prio
% Initializing
x_est = zeros(N,1);
z = y;
tau=1;
delta = M/N;
etafunc = @(x,beta) (x./abs(x)).*(abs(x)-beta).*(abs(x)-beta >0); % (abs(x)-beta >0) is logical num
etafuncdiff = @(x,beta) ((abs(x)-beta >=0));
for iter=1:maxiterx_est = etafunc(x_est + A'*z, tau);z = y - A*x_est + 1/delta*z.*mean(etafuncdiff(x_est + A'*z,tau));tau = tau/delta*mean(etafuncdiff(x_est + A'*z,tau));
end
clc;
clear all;
N = 128; % length of vector to be recovered
M = 64; % number of measurement
A = (1/sqrt(2))*(normrnd(0,1/sqrt(M),M,N) + 1i*normrnd(0,1/sqrt(M),M,N)); % Sensing matrix construction for theroetical bound
x = zeros(N,1); % Initializing sparse vector to be recovered
k = 13; % Sparsity level
uset = randperm(N,k);
x(uset) = rand(k,1) + 1i*rand(k,1); % Sparse vector initialized
noise = sqrt(1/2)*(normrnd(0,1,M,1) + 1i*normrnd(0,1,M,1)); % zero mean, unit covariance complex noise vector
var = 1e-5;
noise = sqrt(var)*noise;
y = A*x + noise; % create measurement
niter = 30; % number of iteration
%% Approximate Message Passing for basis selection
x_est1 = amp(y,k,A,niter);
[x_est2] = AMP_Lplace(y,A,niter);
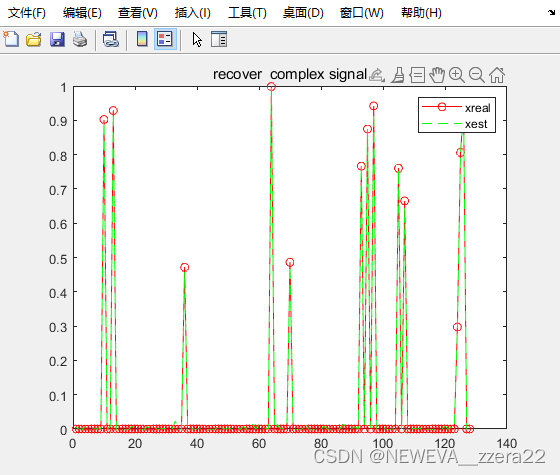
plot(abs(x),'r-o');hold on;
plot(abs(x_est1),'b+-');
plot(abs(x_est1),'g--');
legend('xreal','xest','xestmine');
title('recover complex signal')
nmse1=norm(x_est1-x).^2/(norm(x).^2);
nmse2=norm(x_est2-x).^2/(norm(x).^2);
disp(nmse1)
disp(nmse2)
%[abs(xest) abs(x)]
7、根据论文复现AMPA算法
AMP0和AMPA分别用于BP和BPDN,后者更为通用性,多了一个正则化参数项

function [x_est] = AMP_Lplace(y,A,maxiter,lambda)
%%根据论文写的AMPA算法,效果没有之前的GitHub上的好
[M,N]=size(A);
%% Approximate Message Passing for Laplace Prio
% Initializing
x_est = zeros(N,1);
z = y;
tau=1;
if nargin<4
lambda=0;% regularization parameter
end
delta = M/N;
etafunc = @(x,beta) (x./abs(x)).*(abs(x)-beta).*(abs(x)-beta >0); % (abs(x)-beta >0) is logical num
etafuncdiff = @(x,beta) ((abs(x)-beta >=0));
for iter=1:maxiterx_est = etafunc(x_est + A'*z, tau+lambda);z = y - A*x_est + 1/delta*z.*mean(etafuncdiff(x_est + A'*z,tau+lambda));tau = (lambda+tau)/delta*mean(etafuncdiff(x_est + A'*z,tau+lambda));
end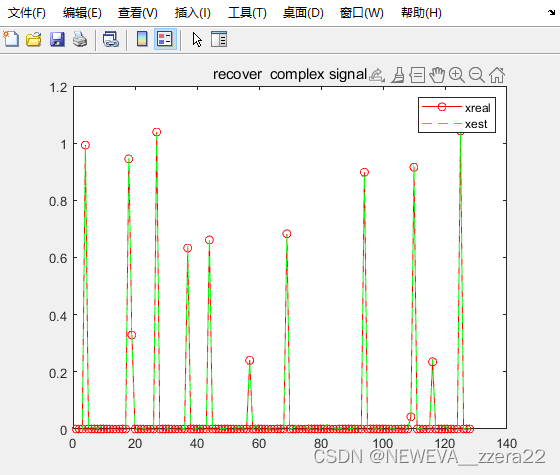
算法感觉不太稳定,有时候会发散。效果还是没有Github上给的代码好。Github上给的代码好像利用了噪声的标准差
sigma = norm(z,2)/sqrt(M);至于为什么,还需要进一步探索。
这篇关于近似消息传递算法(AMP)单测量模型(SMV)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









