密码学基础练习五道 RSA、elgamal、elgamal数字签名、DSA数字签名、有限域(GF)上的四则运算

本文主要是介绍密码学基础练习五道 RSA、elgamal、elgamal数字签名、DSA数字签名、有限域(GF)上的四则运算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.RSA

#include <stdlib.h>#include <stdio.h>#include <string.h>#include <math.h>#include <time.h>#define PRIME_MAX 200      //生成素数范围#define EXPONENT_MAX 200       //生成指数e范围#define Element_Max 127       //加密单元的最大值，这里为一个char, 即1Bytechar str_read[100]="hello world !";      //待加密的明文int str_encrypt[100];      //存放加密后的内容char str_decrypt[100];      //存放解密出来的内容int str_read_len;      //str_read 的长度int prime1, prime2;      //随机生成的两个质数int mod,eular;      //模数和欧拉数int pubKey, priKey;      //公钥指数和私钥指数//生成随机素数int randPrime(){int prime,prime2,i;next:prime=rand()%PRIME_MAX;      //随机产生数if (prime <= 1) goto next;      //不是质数，生成下一个随机数if (prime == 2 || prime == 3)return prime;prime2=prime/2;      //注：prime>=4, prime2 的平方必定大于 prime , 因此只检查小于等于prime2的数for (i=2;i<=prime2;i++)      //判断是否为素数{if(i*i>prime)return prime;if(prime%i==0)goto next;      //不是质数，生成下一个随机数}}// 欧几里德算法，判断a,b互质int gcd(int a, int b){int temp;while (b!=0){temp=b;b=a%b;a=temp;}return a;}//生成公钥，条件是 1< e < 欧拉数，且与欧拉数互质。int randExponent(){int e;while (1){e=rand()%eular;if(e<EXPONENT_MAX)break;}while (1){if(gcd(e, eular)==1)return e;e=(e+1)%eular;if(e==0||e>EXPONENT_MAX)e = 2;}}//生成私钥指数int inverse(){int d,x;while (1){d=rand()%eular;x=pubKey*d%eular;if(x==1){return d;}}}//加密函数void jiami(){str_read_len = strlen(str_read);//从参数表示的地址往后找,找到第一个'\0',即串尾.计算'\0'至首地址的“距离”,即隔了几个字符,从而得出长度.printf("密文是：");for(int i=0;i<str_read_len;i++){int C=1;int a=str_read[i],b=a%mod;for(int j=0;j<pubKey;j++)      //实现加密{C=(C*b)%mod;}str_encrypt[i]=C;printf("%d",str_encrypt[i]);}printf("\n");}//解密函数void jiemi(){int i=0;for(i=0;i<str_read_len;i++){int C=1;int a=str_encrypt[i],b=a%mod;for(int j=0;j<priKey;j++){C=(C*b)%mod;}str_decrypt[i]=C;}str_decrypt[i]='\0';printf("解密文是：%s\n",str_decrypt);}//主函数int main(){srand(time(NULL));while (1){prime1=randPrime();prime2=randPrime();printf("随机产生两个素数:prime1=%d,prime2=%d",prime1,prime2);mod=prime1*prime2;printf("模数:mod=prime1*prime2=%d\n",mod);if(mod>Element_Max)break;      //模数要大于每个加密单元的值}eular=(prime1-1)*(prime2-1);printf("欧拉数:eular=(prime1-1)*(prime2-1)=%d\n",eular);pubKey=randExponent();printf("公钥指数pubKey=%d\n",pubKey);priKey=inverse();printf("私钥指数:priKey=%d\n  私钥为(%d, %d)\n", priKey, priKey, mod);jiami();jiemi();return 0;}

流程图：

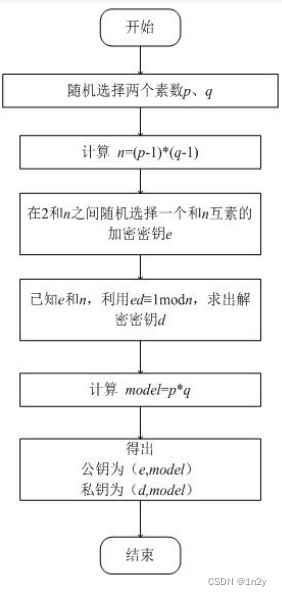
2.elgamal

#include<stdio.h>#include<stdlib.h>#include<math.h>//模重复平方算法,计算a^b mod pint pow_mod(int a,int b,int p){int ans=1;int tmp=a%p;while(b){if(b&1)ans=ans*tmp%p;b>>=1;tmp=tmp*tmp%p;}return ans%p;}//elgamal加密算法，k为任意整数,m为明文，pub为公钥，p为大素数，g为生成元,c1,c2为密文void elgamal_en(int m,int pub,int p,int g,int *c1,int *c2){int k=5;*c1=pow_mod(g,k,p);*c2=m*pow_mod(pub,k,p)%p;}//elgamal解密算法,m_为解密后的数据，p为大素数，g为生成元，c1_为c1模p的逆元，pr为私钥int elgamal_de(int c1,int c2,int pr,int p,int g){int m;int c1_=pow_mod(c1,p-2,p);m=c2*pow_mod(c1_,pr,p)%p;return m;}//判断是否为素数(为了严谨性而存在的函数，题中所给出的测试数据已经是素数了)int is_prime(int p){int i;for(i=2;i<=sqrt(p);i++){if(p%i==0)return 0;}return 1;}int main(){int p=1069;      //必须为素数int g=2;      //本原元do{printf("请输入一个素数:%d\n",p);}while(!is_prime(p));int pr=123;      //用户A的私钥printf("输入用户A的私钥:%d\n",pr);int pub;pub=pow_mod(g,pr,p);printf("用户A的公钥为:%d\n",pub);int m=677;      //明文要小于pint c1,c2;elgamal_en(m,pub,p,g,&c1,&c2);printf("用公钥加密后的密文为:c1=%d,c2=%d\n",c1,c2);int m_=elgamal_de(c1,c2,pr,p,g);printf("用私钥解密后的明文为:%d\n",m_);}

流程图：

3.elgamal数字签名：

#include <stdio.h>#include <stdlib.h>#include <time.h>#include <math.h>int xy[22];int myPow(int a, int b, int m) {int res=1;a%=m;while(b!=0) {if((b&1)==1)res=(res*a)%m;a=(a*a)%m;b>>=1;}return res;}//判断两个数是否互质int Coprime(int a, int b) {return b==0?a:Coprime(b,a%b);}int calculate3(int y,int k,int p) {printf("...%d %d %d\n",y,k,p);int l=1;for(int i = 0; i<k; i++) {l=l*y;l=l%p;}printf("l=%d\n",l);return l;}//求 a mod b 的逆元void exGcd(int a, int b) {if(b==0) {xy[0]=1;xy[1]=0;} else {exGcd(b,a%b);int x=xy[0];xy[0]=xy[1];xy[1]=x-(a/b)*xy[1];}}//主函数int main() {int p=1669,m=101,q=2;        //p为大素数，m为消息，q为本原元int x,y,k,k1,r,a;int k2,ni;int s;srand(time(NULL));      //随机数种子x=15;      //rand()%p-1+2 ;printf("x=%d\n",x);y=myPow(q,x,p);      //y是公开密钥printf("公开密钥y=%d\n",y);k=11;      //rand()%p-1+1 ;while(Coprime(k,p-1)!=1) {k=rand()%p-1+1;}printf("k=%d\n",k);//求r ：r = g^k mod pr=myPow(q,k,p);printf("r=%d\n",r);//加密过程s=calculate3(y,k,p);if(s<0)s=(s+(p-1))%(p-1);s=s*m%p;printf("发送密文(%d,%d)\n",r,s);//解密过程k2=myPow(r,x,p);printf("k2=%d\n",k2);exGcd(r,p);ni=xy[0];if(ni<0)ni=ni+p;printf("ni=%d\n",ni);m=myPow(ni,x,p)*s;printf("m=%d\n",m%p);//签名过程// 计算k^-1 mod p-1exGcd(k,(p-1));k1=xy[0];if(k1<0)k1+=(p-1);printf("k1=%d\n",k1);// s = k^(-1)*(m-rx)(mod p-1)s=(k1*(m-r*x))%(p-1); // (m,r,s)为对消息m的数字签名printf("s=%d\n",s);//s可能为负值，所以要将其转化为正数，利用a%b=(a%b+b)%bif(s<0)s=(s%(p-1)+(p-1))%(p-1);printf("签名为(%d,%d)\n",r,s);if((myPow(y,r,p)*myPow(r,s,p))%p==myPow(q,m,p))printf("接受签名\n");elseprintf("拒绝签名\n");}

流程图：

4.DSA数字签名算法：

#include <stdlib.h>#include <stdio.h>#include <time.h>int xy[22];//乘法逆元int myPow(int a, int b, int m) {int res=1;a%=m;while(b!=0){if((b&1)==1)res=(res*a)%m;a=(a*a)%m;b>>=1;}return res;}int calculate(int h,int p,int q){int a=(p-1)/q;long int k=1;for(int i=0;i<a;i++){k=k*h;}return k%p;}int calculate1(int g,int x,int p){long int k=1;for(int i=0;i<x;i++){k=k*g;}return k%p;}// 求 a mod b 的逆元void exGcd(int a, int b) {if (b == 0) {xy[0] = 1;xy[1] = 0;} else {exGcd(b, a % b);int x = xy[0];xy[0] = xy[1];xy[1] = x - (a / b) * xy[1];}}//主函数int main(){int p=23;short q=11;      //p q为两个大素数，且满足（p-1)能够被q整除(这里为了方便选取了两个较小数，也可取p=7879,q=101)int g,x,y,s,k,m,w,u1,u2,v,h,r;      //对出现的变量进行初始化printf("请输入大素数p=%d和q=%d ,满足（p-1)能够被q整除\n",p,q);srand(time(NULL));      //随机数种子h=12;      //rand()%p-1+2 ;//随机数g=calculate(h,p,q);x=10;      //rand()%p-1+2 ;//私钥y=calculate1(g,x,p);      //计算公钥printf("公钥是(%d,%d,%d,%d)\n",p,q,g,y);printf("私钥为%d\n",x);//签名过程k=9;      //rand()%p-1+2 ;//随机数kr=calculate1(g,k,p)%q;exGcd(k, q);k = xy[0];if(k < 0) k += (p-1);  m=13;s=(m+x*r)*k%q;printf("签名为(%d,%d)\n",r,s);//验证程序exGcd(s,q);w =xy[0];if(w < 0) w += (q);u1=(m*w)%q;u2=r*w%q;v=myPow(g, u1, p)*myPow(y, u2, p)%p%q;printf("(w,u1,u2,v)=(%d,%d,%d,%d)\n",w,u1,u2,v);if(v==r){printf("接受");}else{printf("不接受");}}

流程图:

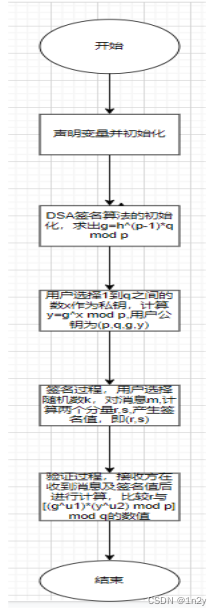
5.有限域（GF）上的加、减、乘法计算器

#include<cstdio>#include<cstdlib>#include<iostream>#include<algorithm>#include<cstring>#include<vector>#include<cmath>#include<bits/stdc++.h>int hex1=0x57,hex2=0x83;void jiafa(int hex1,int hex2){printf("请输入两个十六进制串:%x %x\n",hex1,hex2);printf("\n得到有限域内相加结果 : %#X\n\n",hex1^hex2);}//a减去b，其实就是a加上b的加法逆元，关键是找到b的加法逆元。void chengfa(int hex1,int hex2){int a[16],b[16],s[32];printf("请输入两个十六进制串:%x %x\n",hex1,hex2);int n=hex2,cnt=0;while(n)///转化为二进制{s[cnt++]=n%2;n/=2;}a[1]=0x01,b[1]=hex1;for(int i=2; i<=8; i++)a[i]=a[i-1]<<1;///得到0x01 0x02 0x04 0x08 0x10 0x20 0x40 0x80for(int i=2; i<=8; i++){if(b[i-1]&0x80)///如果最高为为1就对不可约多项式取模,否则直接左移b[i]=((b[i-1]<<1)^0x1B);elseb[i]=b[i-1]<<1;b[i]&=0xFF;///直接取后两位}int hex=0x00;for(int i=7; i>=0; i--){if(s[i]==1)///当二进制的这一位为1的时候才能异或hex^=b[i+1];}printf("\n得到有限域内相乘结果 : %#X\n\n",hex);}int main(){while(1){printf("请选择进行的运算： 0.退出运算  1.加/减法运算  2.乘法运算 \n\n");int ch;scanf("%d",&ch);switch(ch){case 0:system("cls");printf("\n谢谢使用!\n");exit(0);case 1:system("cls");jiafa(hex1,hex2);break;case 2:system("cls");chengfa(hex1,hex2);break;default :system("cls");printf("\n输入错误！请重新输入:\n\n");break;}}return 0;}

流程图：