数字签名专题
安装第三方inf 不含数字签名信息的方法
过程中遇到第三方INF不包含数字签名信息 解决方法:左下角搜索栏输入:高级启动-立即重启-疑难解答-高级选项-启动设置-重启-重启之后,电脑就可以安装未签名驱动了
数字签名是什么?[转]
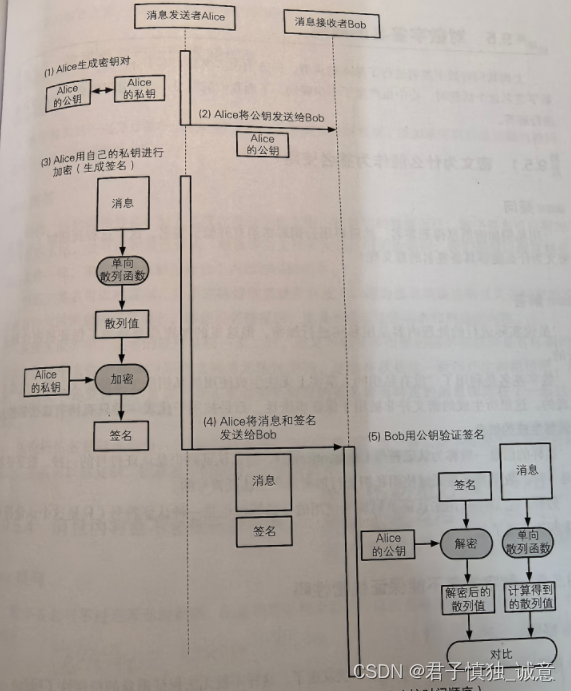
文章来源:http://kan.weibo.com/con/3524902422946278 本文用图片通俗易懂地解释了"数字签名"(digital signature)和"数字证书"(digital certificate)到底是什么。希望多你有帮助。 1. 鲍勃有两把钥匙,一把是公钥,另一把是私钥。 2. 鲍勃把公钥送给他的朋友们----帕蒂、道格
数字签名和数字证书详解
签名 当你在一个纸质文件上写上你的名字,按上你的指纹,就意味着这张纸上的内容经过了你的认可,你的笔迹和指纹就是你身份的证明。这是因为,笔迹很难伪造,而每个人的指纹更是独一无二的。在签名前,我们会检查文件内容有没有歧义、有没有涂改、有没有多余不必要的空白等,确认无误后再写下我们的名字,而收到签名后文件的人,再次对文件内容及签名进行检查,以确保文件内容的有效性和完整性。 因此,签名可以用来认证签名
windows下安装pyenv+解决pyenv install时“未对文件进行数字签名”或“pyenv : 无法加载文件在此系统上禁止运行脚本”的问题
安装pyenv 按照该博主的帖子,安装好pyenv-windows并配置好环境变量: http://t.csdnimg.cn/siQMH 但是执行pyenv install命令时遭遇了如下问题,现在记录一下。 问题1:pyenv : 无法加载文件在此系统上禁止运行脚本。 刚拿到电脑,在电脑上运行`power shell``的同学更可能遇到这个问题。 主要问题出在电脑的执行策略需要更改,可
数字签名算法---加密学习笔记(五)
介绍 签名:就有安全性,抗否认性 数字签名:带有密钥(公钥,私钥)的消息摘要算法 作用: 1. 验证数据的完整性 2. 认证数据来源 3. 抗否认 数字签名遵循:私钥签名,公钥验证 常用的数字签名算法:RSA,DSA,ECDSA RSA 介绍: 是经典算法,是目前为止使用最广泛的数字签名算法。 RSA数字签名算法的密钥实现与RSA的加密算法是一样的,算法的名称都叫RSA。密钥的产生
高级数字签名之椭圆曲线数字签名算法(ECDSA)
@TOC 1. 算法简述 该算法是微软操作系统及办公软件的序列号验证算法。 ECDSA(Elliptic Curve Digital Signature Algorithm, 椭圆曲线数字签名算法) 于1999年作为ANSI标准, 并于2000年成为IEEE和NIST标准。 ECDSA算法具有速度快、强度高、签名短等有点。 3. 代码实现 Java中未对该算法做实现, 而在Bouncy
数字签名标准算法——DSA
数字签名标准算法——DSA 1. 算法简述2.模型分析3. 代码实现3.1 算法实现3.2 测试代码3.3 运行结果 1. 算法简述 RSA为经典数字签名算法 数字签名标准(Digital Signature Standard, DSS), DSS本质是ElGamal数字签名算法,DSS使用的算法成为数字签名算法(Digital Signature Algorithm, DSA
数字签名算法之RSA
数字签名算法之RSA 1.数字签名简述2. 模型分析3. 代码实现3.1 签名算法实现3.2 测试代码3.3 运行结果 1.数字签名简述 数字签名算法可以看做是一种带有密钥的消息摘要算法,并且这种密钥包含了公钥和私钥。也就是说数字签名算法是非对称加密算法和消息摘要算法的结合体。 数字签名算法是公钥基础设施(PKI)以及许多网络安全机制(SSL/TLS、VPN等)的基础。 数
最新的kali Linux源,解决apt update报错说没有数字签名
原因: 国内源的地址大部分都是http开头,这些地址早就无法使用。 解决方案: wget archive.kali.org/archive-key.asc //下载签名 apt-key add archive-key.asc //安装签名 另外,需要kali Linux更换最新的源地址:
接口安全--http数字签名
为了保证http请求数据的安全性和防篡改性。我们通常要对请求参数进行一些加密。 加密规则可以根据双方接口协商定义。这里举一个常用的加密协议例子。 1. sign加密协议 接口协议中通常会提供一个 appKey作为唯一的标识。 appSecret作为接入密钥。 例如:appkey=hh appSecret=39ertfefdsg406c7c36592d42022aaecc 请求路径 h
数字证书及其简单数字签名的实现
<!--[if !supportLists]-->1、<!--[endif]-->引导语/数字证书的应用 提到数字证书,大家首先可能想到这些。 然而其实这些也是数字证书运用很广泛的地方,可以说,数字证书是整个信息时代网络安全及其有力的一种保障。 我们可以简单的用一种很直接的方法查看我们的证书,比如右击一个exe类型的文件,打开文件的属性,然后你可以很清楚的看到数字证书这个选项。一般合格的企业都
数字证书及其简单数字签名的实现(java实现)
<!--[if !supportLists]-->1、<!--[endif]-->引导语/数字证书的应用 提到数字证书,大家首先可能想到这些。 然而其实这些也是数字证书运用很广泛的地方,可以说,数字证书是整个信息时代网络安全及其有力的一种保障。 我们可以简单的用一种很直接的方法查看我们的证书,比如右击一个exe类型的文件,打开文件的属性,然后你可以很清楚的看到数字证书这个选项。一般合格的企
数字签名是什么? 对称加密 与非对称加密
原址:点击打开链接 (一)对称加密(Symmetric Cryptography) 对称加密是最快速、最简单的一种加密方式,加密(encryption)与解密(decryption)用的是同样的密钥(secret key),这种方法在密码学中叫做对称加密算法。对称加密有很多种算法,由于它效率很高,所以被广泛使用在很多加密协议的核心当中。 对称加密通常使用的是相对较小的密钥,一般小于256 bit
现代密码学-数字签名
从消息认证码到数字签名 前面讲到,消息认证码无法防止否认,A,B之间共享密钥计算出MAC,A,B都能计算出MAC,对于第三方C来说,他无法证明这个MAC是A计算的还是B计算的。 通过数字签名解决问题。 A,B各自使用不同的密钥-公钥密码,A用私钥生成一个签名,B可以用A公开的公钥进行验证。 签名的生成和验证 数字签名中的两种行为: 生成消息签名 验证消
使用Bouncy Castle生成数字签名、数字信封
Bouncy Castle(轻量级密码术包)是一种用于 Java 平台的开放源码的轻量级密码术包,它支持大量的密码术算法,并提供 JCE 1.2.1 的实现。最近项目上正好用到了Bouncy Castle,用于生成数字签名、数字信封,去网上找了很久,都没有找到合适的案例,而Bouncy Castle本身的文档也不多,最有用的就是官网上的Java Doc文档,因为这个问题也困扰了我好几天,最后还是通
数字签名:确保信息完整性和身份验证的关键技术
在数字时代,信息的安全性和真实性变得至关重要。数字签名作为一种电子形式的签名,提供了一种验证信息来源和确保信息完整性的方法。本文将深入探讨数字签名的概念、工作原理、应用场景以及它如何帮助提高网络安全性。 数字签名的概念 数字签名是一种加密机制,它允许个人或实体对电子文档或消息进行签名,以证明其来源并确保信息在传输过程中未被篡改。与传统的纸质签名相比,数字签名提供了更高的安全性和可验证性
加密/解密--数字信封/数字签名/数字证书
what 加密 加密:加密就是对原来为明文的文件或数据按某种算法进行处理,使其成为一 段不可读的代码,通常称为 “密文”。从而达到保护数据不被非法窃取的目的。 解密 数据加密的逆向过程,将加密的数据转换为明文 加/解密工作机制 对称密钥算法(共享密钥算法) ---使用同一个密钥对数据进行加密和解密 这就意味着对称加密技术要通信双方需要事先共享相同的密钥,若攻击者得到私钥就能截获密文
一种android安全机制-数字签名
本机制采用不对称加密算法。详细介绍如下: android客户端: 首先客户端要生成一串很长的base64串,同时将该串保存到key-value中,然后客户端带着这个base64串发送一个网络请求,从后台将数字签名的公钥下载下来,即证书下载,接下来客户端将证书导入,导入的证书应是可以获取的。 证书已经导入到前端,接下来就该用证书对我们要加密的数据进行数字签名了,将要加密的数据与之
和安全有关的那些事(非对称加密、数字摘要、数字签名、数字证书、SSL、HTTPS)
对于一般的开发人员来说,很少需要对安全领域内的基础技术进行深入的研究,但是鉴于日常系统开发中遇到的各种安全相关的问题,熟悉和了解这些安全技术的基本原理和使用场景还是非常必要的。本文将对非对称加密、数字摘要、数字签名、数字证书、SSL、HTTPS等这些安全领域内的技术进行一番简要的介绍,解释他们之间的关系,同时补充一些周边话题。 0. 概览--常用安全技术及其之间的关联 安全领域的技术
网络加密解密原理(三) RSA加密解密及数字签名Java实现
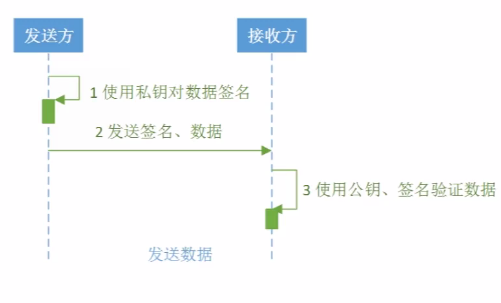
流程分析: 甲方构建密钥对儿,将公钥公布给乙方,将私钥保留。甲方使用私钥加密数据,然后用私钥对加密后的数据签名,发送给乙方签名以及加密后的数据;乙方使用公钥、签名来验证待解密数据是否有效,如果有效使用公钥对数据解密。乙方使用公钥加密数据,向甲方发送经过加密后的数据;甲方获得加密数据,通过私钥解密。 按如上步骤给出序列图,如下: 通过java代码实现如
网络加密解密原理(二) RSA加密解密及数字签名Java实现
RSA公钥加密算法 是1977年由 罗纳德·李维斯特 (Ron Rivest)、阿迪·萨莫尔 (Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。当时他们三人都在麻省理工学院 工作。RSA就是他们三人姓氏开头字母拼在一起组成的。 RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密
密码学基础练习五道 RSA、elgamal、elgamal数字签名、DSA数字签名、有限域(GF)上的四则运算
1.RSA #include <stdlib.h>#include <stdio.h>#include <string.h>#include <math.h>#include <time.h>#define PRIME_MAX 200 //生成素数范围#define EXPONENT_MAX 200 //生成指数e范围#define Element_Max 127


![数字签名是什么?[转]](https://i-blog.csdnimg.cn/blog_migrate/a4c26d1e5885305701be709a3d33442f.gif)