rsa专题
研究人员在RSA大会上演示利用恶意JPEG图片入侵企业内网
安全研究人员Marcus Murray在正在旧金山举行的RSA大会上公布了一种利用恶意JPEG图片入侵企业网络内部Windows服务器的新方法。 攻击流程及漏洞分析 最近,安全专家兼渗透测试员Marcus Murray发现了一种利用恶意JPEG图片来攻击Windows服务器的新方法,利用该方法还可以在目标网络中进行特权提升。几天前,在旧金山举行的RSA大会上,该Marcus现场展示了攻击流程,
apk中签名文件探究(*.SF, *.MF,*.RSA)
文章来源: 作者:嘟嘟小灰 链接:https://www.jianshu.com/p/e07da93acf98 来源:简书 1、取一个apk,然后进行不同签名,生成1.apk、2.apk,并提取META-INF里面的文件进行比对 def calc_sha1(data):sha1obj = hashlib.sha1()if not isinstance(data, (bytear
ssh登录服务器报错“no matching host key type found. Their offer: ssh-rsa,ssh-dss”解决方法
这个错误表明你尝试使用 ssh 连接到远程服务器时,客户端和服务器之间没有匹配的 host key 类型。具体来说,远程服务器提供了 ssh-rsa 和 ssh-dss 类型的 host key,但你的 SSH 客户端配置可能不再支持这些较旧的算法。最近的 OpenSSH 版本默认禁用了不够安全的算法,如 ssh-rsa 和 ssh-dss。 解决方法 临时启用 ssh-rsa: 你可以在
rsa加解密,js加密,php解密
PHP服务端与客户端交互、提供开放api时,通常需要对敏感的部分api数据传输进行数据加密,这时候rsa非对称加密就能派上用处了,下面通过一个例子来说明如何用php来实现数据的加密解密 加密解密的第一步是生成公钥、私钥对,私钥加密的内容能通过公钥解密(反过来亦可以)下载开源RSA密钥生成工具openssl(通常Linux系统都自带该程序),解压缩至独立的文件夹,进入其中的bin目录,
二叉树 链表 + RSA
1 Base64: 与其说是加密解密,还不如说是编码和解码吧,这种加密方式只能防止人一眼看穿 MD5: 加密是只有加密,没有解密方法,即不可逆转。通过MD5加密,会生成一串字符 http://blog.csdn.net/oskytonight/article/details/25058695 2R RSA: 主要用于公钥加密私钥解密、私钥签名公钥验签。 有了公钥和私钥,就能
【RSA】简单说说什么是RSA非对称加密
希望文章能给到你启发和灵感~ 如果觉得文章对你有帮助的话,点赞 + 关注+ 收藏 支持一下博主吧~ 阅读指南 开篇说明一、基础环境说明1.1 硬件环境1.2 软件环境 二、什么是非对称加密2.1 常见的非对称加密有哪些?2.2 哪些场景适合使用非对称加密?2.3 和对称加密的区别是什么? 三、编程中如何实现对称和非对称加密? 开篇说明 加密中,我们常常会见到多种加密形式
openssl RSA 密钥(key)、证书签名请求(csr)、证书(cer)的生成和例子
1. RSA 密钥(key)、证书签名请求(csr)、证书(cer)的生成顺序 2. 具体操作 a. 生成 RSA 密钥(私钥) openssl genrsa -aes256 -out ca.key 2048 b. 生成证书签名请求(csr) # C-----国家(Country Name)# ST----省份(State or Province Name)# L----城市(
RSA加密解密算法认识及signln_resolve
RSA初步了解 一、首先认识rsa是一种非对称加密算法。 对称加密:加密解密使用同一个密钥,加密者接受信息采用密钥加密,而到破译者手中还是使用这份密钥。这种方式的优点是加密效率高、加解密速度快,但是缺点是密钥需要共享,如果密钥被泄漏,则加密无效。 非对称加密:加密解密使用不同的密钥,加密使用的是公钥,解密使用的是私钥,因为公钥可以公开,所以只有私钥知道的加密信息能够被解密,这种方式的优点是安
【算法进阶2-动态规划】最长公共子序列、欧几里得算法-分数、RSA算法-密码于加密
1 最长公共子序列 2 欧几里得算法 2.1 欧几里得算法-分数 3 RSA算法-密码于加密 1 最长公共子序列 -个序列的子序列是在该序列中删去若干元素后得 到的序列。例:“ABCD”和“BDF”都是“ABCDEFG”的子序列最长公共子序列(LCS)问题:给定两个序列X和Y,求X和Y长度最大的公共子序列。例:X="ABBCBDE" Y="DBBCDB" LCS(X,Y)="BB
Linux中Git推送报错Permissions 0644 for ‘/root/.ssh/id_rsa‘ are too open
准备在Linux上配置秘钥,方便Git上传代码到GitHub。 但是秘钥(id_rsa文件)是从本地Windows环境上传到Linux服务器上面的,在执行推送时报错了,如下: # git push -u origin mainThe authenticity of host 'github.com (20.205.243.166)' can't be established.ECDSA k
RSA非对称性加密02: 加密redis的连接密码(下)
全文目录,一步到位 1.前言简介1.1 专栏传送门1.1.2 上文传送门 2. 使用方式2.1 使用druid自带的RSA加密工具2.1.1 引入druid依赖2.1.2 原yml配置(对比使用)2.1.2 新yml配置 2.2 springboot的redis配置类2.2.1 例如在RedisConfig中2.2.2 设置序列化与反序列化代码示例如下: 2.3 如何加密与解密 `(方法
golang RSA 解密前端jsencrypt发送的数据时异常 crypto/rsa: decryption error 解决方法
golang中 RSA解密前端(jsencrypt)发来的密文后出现 "crypto/rsa: decryption error" , 这个问题首先需要确认你的私匙和公匙是否匹配, 如果匹配 那检查入参数据类型, 前端发送来的rsa加密后的数据一般都是经过base64编码后的, 在后端进行RSA解码时需要对前端发送的数据进行base64解码! crypto/rsa: decryption
C# unity 中关于RSA加密字节太长的问题
using System; using System.Collections; using System.Collections.Generic; using System.IO; using System.Security.Cryptography; using System.Text; using UnityEngine; //RSA加密字节太长的问题 public class Segment
自定义类加载器加载加密jar包,使用Reflections扫描自定义加载器加载的Class,RSA加密解密签名AES密文,AES加密解密文件
为什么要做这个工作: 游戏私服是游戏人最讨厌的一件事,而游戏私服基本上都是内部人员把内部的自启服务器泄露出去,我们现在做的就是,内部发行的服务器版本是加密后的二进制文件,必须用给定的RSA秘钥才能解密二进制文件,然后 再使用自定义类加载器进行加载,在整个过程中都是流操作,不会生成class文件,就能防止内部发行的服务器被拷贝。这样并不能完全防止服务器泄露,如果有心人拿到秘钥,拿到加密后的
python3 paramiko 基于RSA私钥远程执行ssh、上传、下载文件
介绍 paramiko 遵循SSH2协议,支持以加密和认证的方式,进行远程服务器的连接,可以实现远程文件的上传,下载或通过ssh远程执行命令。 项目地址:https://github.com/paramiko/paramiko 官方文档:http://docs.paramiko.org/ 使用pip3安装 pip3 install paramiko 上一篇章已经讲诉了使用密码访问的方式
常用加密算法之 RSA 简介及应用
引言 相关博文: Spring Boot 开发 – 常用加密算法简介(一)常用加密算法之 SM4 简介及应用 一、RSA算法简介 RSA (Rivest-Shamir-Adleman) 算法是一种非对称加密技术,由Ron Rivest、Adi Shamir和Leonard Adleman在1977年发明。它基于大数质因数分解的困难性,提供了一种安全的数据加密和解密方法。 1. 密钥生成
RSA非对称的加密算法
首先RSA是一个非对称的加密算法,所以在使用该算法加密解密之前,必须先行生成密钥对,包括公钥和私钥 JDK中提供了生成密钥对的类KeyPairGenerator,实例如下: public static Map<String, Object> genKeyPair() throws Exception { // 获取公钥私钥密钥对的生成器 KeyPairGenerator kpg
python3 rsa加密
加密首先要有public key,如果加密后的内容用来做http请求,可能还需要对其quote一下。 def test():public_key = """-----BEGIN PUBLIC KEY-----*******MIICIjANBgkqhkiG9w*******-----END PUBLIC KEY-----"""import rsaimport base64from urlli
RSA —非对称加密算法
常见的数字加密方式分为两类:对称加密 和 非对称加密。 对称加密,又称为私钥加密,指的是加密和解密使用同一个密钥的方式。其特点是加密和解密过程简单、快速,并且只需要一个密钥。常见的对称加密算法包括DES、AES等。然而,由于使用的是同一个密钥,如果密钥被黑客拦截,信息就很容易被破译。 非对称加密,又称为公钥加密,是指使用一对非对称密钥进行加密的方式,其中一个密钥是公钥
RSA密码系统的特定密钥泄露攻击与Coppersmith方法的应用
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。 RSA密码系统作为当前最广泛使用的公钥加密算法之一,其安全性依赖于大整数分解问题的困难性。然而,随着计算能力的提高和算法优化,特别是Coppersmith方法的出现,使得在特定条件下对RSA系统进行密钥恢复成为可能。本文将深入探讨Coppersmith方法
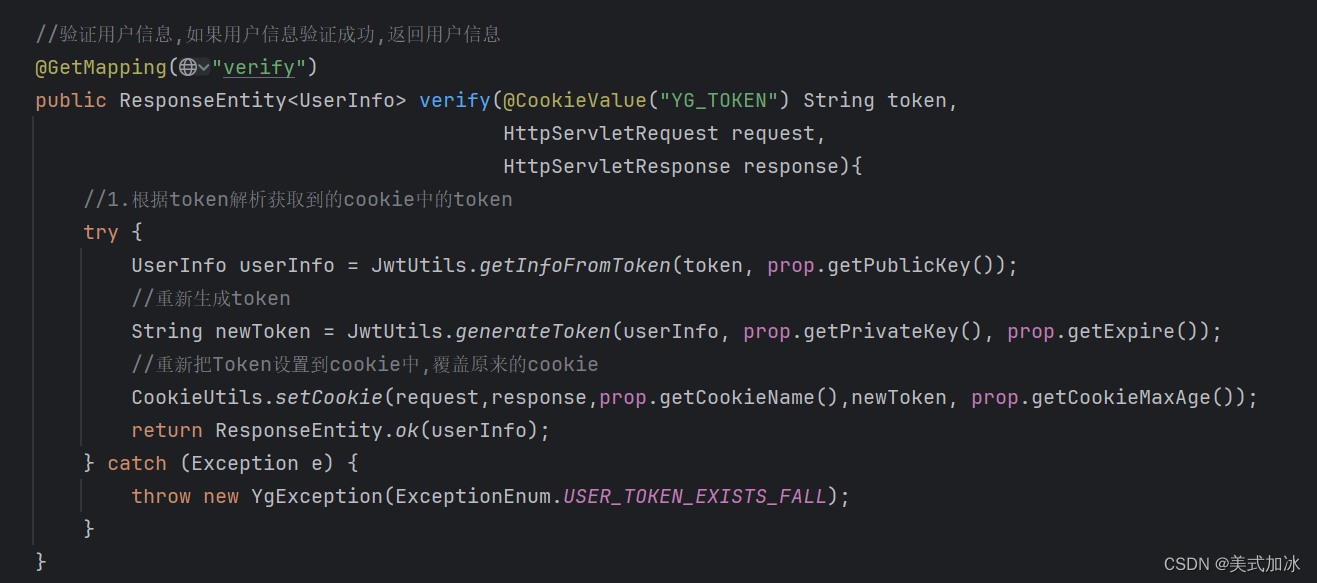
JWT整合Gateway实现鉴权(RSA与公私密钥工具类)
一.业务流程 1.使用RSA生成公钥和私钥。私钥保存在授权中心,公钥保存在网关(gateway)和各个信任微服务中。 2.用户请求登录。 3.授权中心进行校验,通过后使用私钥对JWT进行签名加密。并将JWT返回给用户 4.用户携带JWT访问 5.gateway直接通过公钥解密JWT进行验证 二.RSA测试Demo JWT包含三部分数据 header头部分-Payload载荷(包含用户
数字签名算法之RSA
数字签名算法之RSA 1.数字签名简述2. 模型分析3. 代码实现3.1 签名算法实现3.2 测试代码3.3 运行结果 1.数字签名简述 数字签名算法可以看做是一种带有密钥的消息摘要算法,并且这种密钥包含了公钥和私钥。也就是说数字签名算法是非对称加密算法和消息摘要算法的结合体。 数字签名算法是公钥基础设施(PKI)以及许多网络安全机制(SSL/TLS、VPN等)的基础。 数
什么是RSA国产数字证书?
一位朋友向我打听什么是RSA国产证书? 我们用的较多说法是,国际算法的RSA证书,国密算法的SM2证书,那么有没有RSA国产证书呢? RSA国产证书的提法并不标准,它来源一个安全通告,2019年11月30日 首都网警《关于OPENSSL加密组件存在重大风险隐患的预警通报》。全文如下: 近日,据国家网络与信息安全信息通报中心监测发现,互联网SSL协议实现组件OPENSSL部分版本存在重大安全