本文主要是介绍《R语言与农业数据统计分析及建模》学习——logistic回归和poisson回归,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
普通线性回归通常用来描述变量y与x之间的线性关系:
普通线性模型的假设是:响应变量y是连续型变量而且,服从正态分布分布。但在很多现实情况y并不是正态分布,如:二值问题/多分类问题,计次问题等,这些问题都是广义线性回归的范畴。广义线性回归用于解决因变量不是正态分布的问题。不同的广义线性回归类型,使用不同的连接函数,如下:
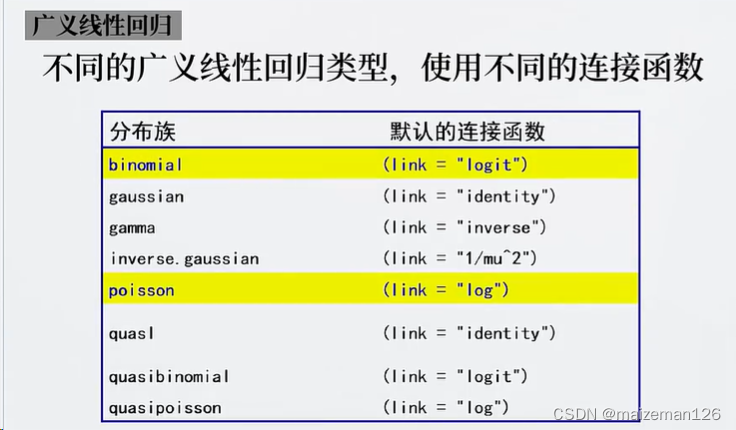
一、Logistic回归
Logistic回归通过使用其固有的logistic函数估计概率,来衡量因变量与一个或多个资变啊领之间的关系。
R中使用glm()函数拟合Logistic模型。调用格式如下:
glm(formula,family=family.generator,data=data.frame)
该函数与普通线性回归函数lm()的差异是,需要设置分布族参数(family),即连接函数。
# 导入数据集
# 某省份农田的产量、降水、温度数据集
df<-read.csv("Logistic.csv")
# 展示数据集
str(df)
# 建立广义线性回归模型
# 因变量转为因子型
df$yield<-as.factor(df$yield)
log_glm<-glm(yield~rain+temp,data=df,family="binomial")
summary(log_glm)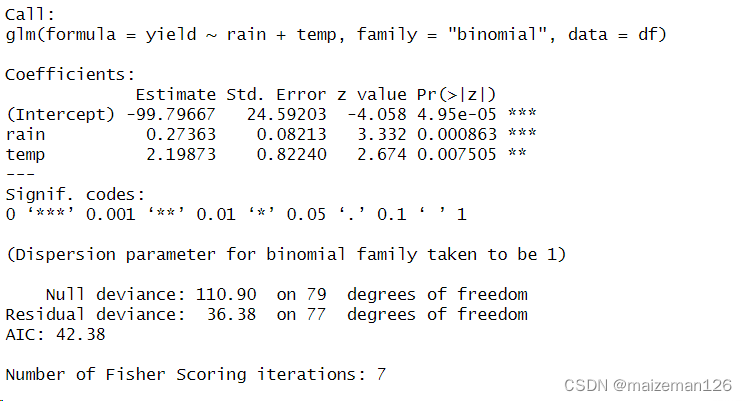
# 用建立的模型进行预测
df_new<-data.frame(temp=c(16.5,18.9),rain=c(210,246))
y_pred<-predict(object=log_glm,newdata=df_new,type="response")
y_pred
结果:预测值返回的是概率值。1的产量为y的概率为0.0023,2的产量为y的概率是0.9998
二、Poisson回归
Poisson回归是假设y服从泊松分布,使用连接函数为log(λ),来衡量因变量与自变量之间的关系。
R中使用glm()函数拟合Poisson模型。
# 导入数据
# 诱导仙客来开花的试验数据
df<-read.csv("Poisson.csv")
# 数据展示
head(df)
# Variety(品种:哑元1~4)
# Regimem(温度方案:哑元1~4)
# Day(白天温度:摄氏度)
# Night(夜间温度:摄氏度)
# Fertilizer(施肥水平:哑元1~4)
# Flowers(花的数目)# 将变量转为因子型
df$Variety<-as.factor(df$Variety)
df$Regimem<-as.factor(df$Regimem)
df$Fertilizer<-as.factor(df$Fertilizer)# 建立Poisson回归模型
fit<-glm(Flowers~Variety+Regimem+Fertilizer,family=poisson(link="log"),data=df)
# 对拟合结果进行卡方检验
anova(fit,test="Chisq")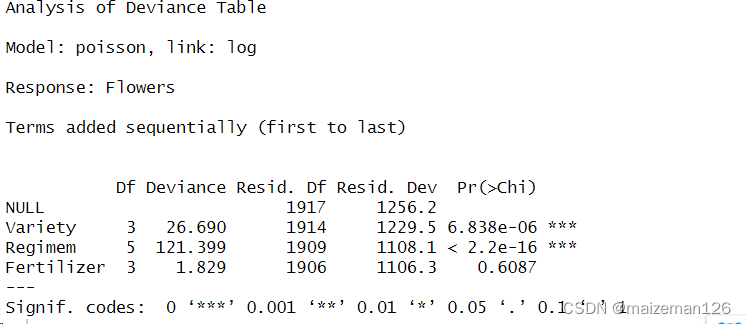
结果显示,fertilizer对flowers的影响不显著,下面尝试逐步回归对模型进行精简。
# 尝试逐步回归
fit_new<-step(fit)
# 比较逐步回归前后两个模型的结果
anova(fit,fit_new,test="Chisq")
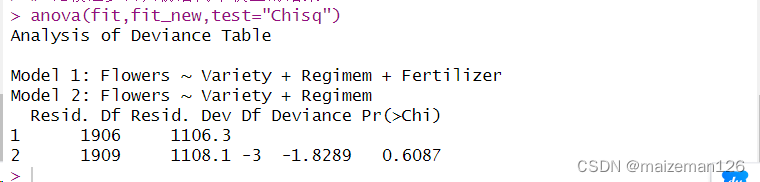
逐步回归剔除了Fertilizer变量,而且两个回归模型对比分析,二者之间差异不显著,所以可以使用逐步回归后的模型。
这篇关于《R语言与农业数据统计分析及建模》学习——logistic回归和poisson回归的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





