本文主要是介绍smac 路径优化器分析——距离成本和代价地图成本分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考
泰勒级数直观详解
前向差分,后向差分,中心差分
相关文章
smac 路径优化器分析——平滑度成本分析
smac 路径优化器分析——曲率成本分析
距离成本
距离成本函数
用优化后的点与原路径点的欧氏距离的平方作为成本。
下图中蓝色原点是原路径点,红色原点是优化后路径点。
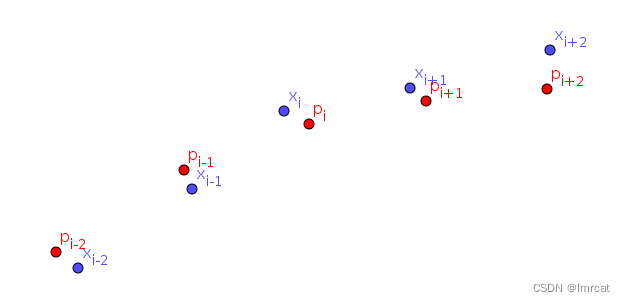
距离成本函数为:
是优化后的路径点,
是原路径点。
距离成本梯度函数
距离成本函数表示为:
偏导数可以得到:
代价地图成本
代价地图成本函数
Smac 直接使用路径点所在的 costmap2D 地图栅格的代价值的平方作为代价地图成本。
下图中黄色圆点表示路径点,背景是 costmap2D 地图。
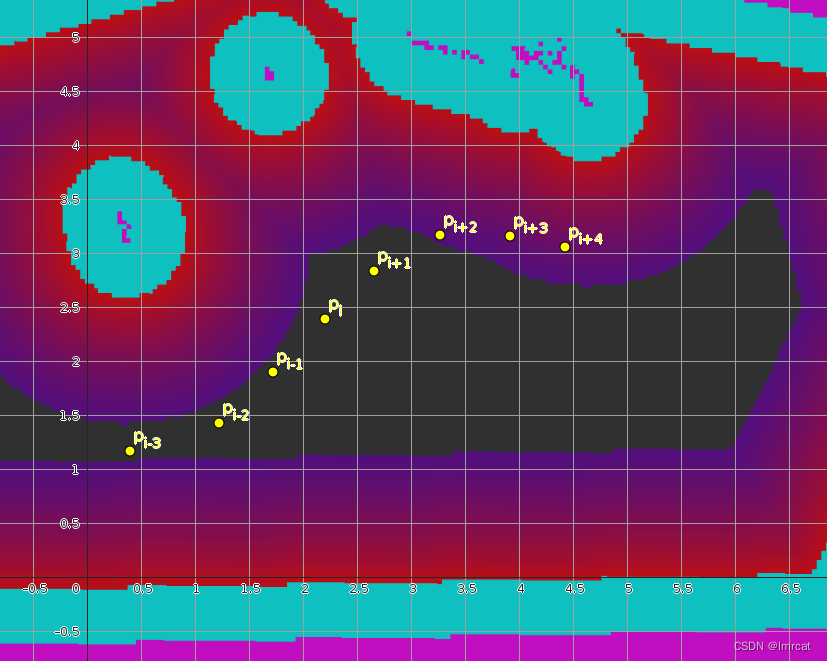
代价地图成本函数为:
代价地图成本梯度函数
按源码提示是根据泰勒级数展开计算的,但是我颠来倒去都推导不出源码的公式。゚(TヮT)゚。
如果是使用中心差分法,那么 Δh 步进越小,计算得到的梯度才越精确。在栅格地图中最小自变量偏移是 1 个栅格。
令 ,那么代价地图成本为
,根据中心差分法,在点 a 处对 x 求偏导有
同理,在点 a 处对 y 求偏导有
代价地图梯度函数优化对比
smac 的 smoother 路径平滑器仅打开代价地图成本和距离成本函数和成本梯度函数的优化对比。
绿色路径是随机生成的路径,红色路径是 smac 源码优化后的路径,黄色路径是使用本文代价地图成本梯度函数优化后的路径。由于路径的起点和终点并不参与优化过程,所以起点和终点的位置始终不会变,这里的路径发布我去掉了优化后路径的终点。
新旧对比代价梯度-红旧黄新
为了观察清楚代价地图成本优化效果,costmap2d 的膨胀半径增大,同时将代价缩放因子调整到合适的参数,使得代价值能够平缓地在膨胀半径边缘降到最低。
这篇关于smac 路径优化器分析——距离成本和代价地图成本分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






