动态规划——斐波那契数列模型：面试题08.01.三步问题

本文主要是介绍动态规划——斐波那契数列模型：面试题08.01.三步问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

题目链接：面试题08.01.三步问题

如果n是0走法可能是1也可能是0，所以本题范围并不需要考虑直接从1开始即可

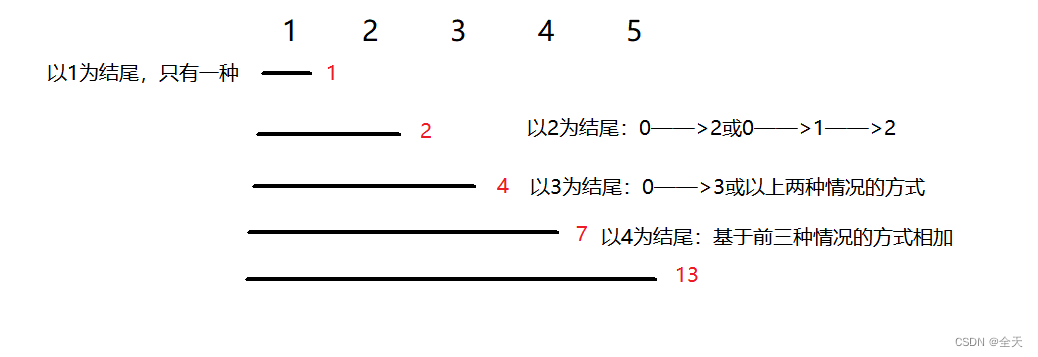
因为以3为结尾有直接从0到3的方式，其他的方式则需要经过前面的阶梯，所以则是基于前面的方式来计算当前位置的方式，以此类推。
PS：答案可能过大，所以题目要求需要取模1e9 + 7。

算法原理

1.状态表示

经验+题目要求：经验一般是以…开始，以…结尾。
dp[i]:表示到达i位置时，一共有多少种方式。

2.状态转移方程

dp[i] = dp[i -1] + dp[i - 2] + dp[i - 3]

3.初始化

dp[1] = 1,dp[2] = 2,dp[3] = 4

4.填表顺序

从左往右

5.返回值

dp[n]

代码实现

C++

class Solution {
public:int waysToStep(int n) {//单独处理边界条件if(n < 3)return n;else if(n == 3)return 4;//1.创建dp表vector<int> dp(n + 1);const int MOD = 1e9 + 7;//2.初始化dp[1] = 1,dp[2] = 2,dp[3] = 4;//3.填表for(int i = 4;i <= n;++i){//处理溢出问题dp[i] = ((dp[i - 3] + dp[i - 2]) % MOD + dp[i - 1]) % MOD;}//4.返回值return dp[n];}
};

Java

class Solution {public int waysToStep(int n) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4.返回值int MOD = (int) 1e9 + 7;// 处理⼀下边界情况if (n == 1 || n == 2)return n;if (n == 3)return 4;int[] dp = new int[n + 1];dp[1] = 1;dp[2] = 2;dp[3] = 4;for (int i = 4; i <= n; i++)//处理溢出问题dp[i] = ((dp[i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;return dp[n];}
}

这篇关于动态规划——斐波那契数列模型：面试题08.01.三步问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---