本文主要是介绍CU-Mamba:具有通道学习功能的选择性状态空间模型用于图像恢复,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
CU-Mamba:具有通道学习功能的选择性状态空间模型用于图像恢复
- 摘要
- Introduction
- Related Work
- Method
CU-Mamba: Selective State Space Models with Channel Learning for Image Restoration
摘要
重建退化图像是图像处理中的关键任务。尽管基于卷积神经网络(CNN)和Transformer的模型在该领域中非常普遍,但它们存在固有的局限性,比如对长距离依赖的建模不足以及高计算成本。
为了克服这些问题,作者引入了通道感知U型Mamba(CU-Mamba)模型,它将双状态空间模型(SSM)框架融入到U-Net架构中。
CU-Mamba使用空间SSM模块进行全局上下文编码,并采用通道SSM组件来保持通道相关性特征,两者相对于特征图大小都具有线性计算复杂性。
广泛的实验结果验证了CU-Mamba相对于现有最先进方法的优越性,强调了在图像恢复中同时融合空间和通道上下文的重要性。
Introduction
图像恢复是数字图像处理中的基本任务,旨在从各种退化(如噪声、模糊和雨迹)损害的图像中重建高质量图像。最近的进展凸显了卷积神经网络(CNNs)[1, 2, 3]和基于Transformer的模型[4, 5, 6, 7]在此领域的有效性。CNN利用层次结构,擅长捕捉图像内的空间层次。Transformer模型最初是为自然语言处理设计的,但已经显示出对视觉理解的积极成果,例如Vision Transformer[8]。Transformer模型采用自注意力机制,特别擅长建模长距离依赖。这两种方法在许多图像恢复任务中均取得了最先进的结果[9, 10, 11]。
然而,卷积神经网络(CNNs)和基于Transformer的模型都有其局限性。尽管CNN在局部特征提取方面很有效,但由于其有限的感受野,它们通常难以捕捉图像中的长距离依赖关系。相比之下,尽管Transformers通过全局注意力模块缓解了这个问题,但它们相对于特征图大小的计算成本是二次的。此外,Transformers可能会忽略对于有效图像恢复至关重要的细粒度局部细节。
为了解决这些限制,近期的进展引入了结构化状态空间模型(SSMs),特别是Mamba模型[12, 13],作为图像识别网络的有效构建模块[14, 15]。通过高效地通过输入依赖的选择性SSMs[13]压缩全局上下文,Mamba保持了全局感受野的好处,同时与输入标记的线性复杂度进行操作。这种方法已经在各种语言和视觉任务中展示了卓越的性能,超过了基于CNN和Transformer的模型[13]。然而,大多数视觉Mamba模型将SSM块独立应用于每个特征通道,这可能导致通道间信息流的丢失[16],这对于在图像恢复中压缩和重建图像细节尤其关键。
为了解决上述挑战,作者提出了一个通道感知型U形Mamba(CU-Mamba)模型用于图像修复。在图像修复的传统U-Net结构[17]之上,CU-Mamba通过Mamba模块实现了全局感受野,同时保持了通道特定的特征。作者在架构中使用了一个空间状态空间模型模块,以线性计算复杂度有效地捕获图像中的长距离依赖关系,确保了对全局上下文的全面理解。此外,作者还实现了一个通道状态空间模型组件,在U-Net的特征图压缩和后续上采样过程中增强通道间的特征混合。这种双重方法使得CU-Mamba模型能够在捕捉广泛的空间细节和保持复杂的通道间相关性之间达到微妙的平衡,从而显著提高了修复图像的质量和准确性。
总的来说,这项工作主要贡献如下:
作者引入了通道感知U形玛巴(Channel-Aware U-Shaped Mamba,简称CU-Mamba)模型,通过结合双状态空间模型(State Space Model,简称SSM)来为图像恢复任务丰富U-Net的全球上下文和通道特定特征。
作者通过详细的消融研究验证了空间和通道SSM模块的有效性。
作者的实验表明,CU-Mamba模型在多种图像恢复数据集上取得了有希望的性能,超越了当前的SOTA方法,同时保持了较低的计算成本。
Related Work
基于CNN的方法: 近几年,基于CNN的模型[3, 11]一直是图像恢复的基本架构。这些模型相比于传统的技术[18](后者严重依赖手工制作特征和先验知识)实现了实质性的改进。在基于CNN的模型中,具有跳跃连接的U形编码器-解码器网络[19]因其分层多尺度架构和残差特征表示,在各种图像恢复任务中展现出了强大的竞争力。
基于Transformer的方法: CNN中的固有局部感受野限制了捕捉长距离依赖的能力。这一挑战促使采用Transformer模型[8, 20],它们利用全局自注意力机制来封装图像中的长距离交互。现在,Transformer模型广泛应用于低级视觉任务中,如超分辨率[7]、图像去噪[21]、去模糊[22]和去雨[23]。为了减少注意力机制中的二次计算复杂度,自注意力在局部窗口[24]或通道维度[25]上执行。尽管进行了架构设计,但由于自注意力模块的内在机制,计算开销依然很高。
视觉结构化状态空间模型: 最近的创新包括将状态空间模型(SSMs)[12, 13]集成到图像识别流程中,正如Vision Mamba [15]所示。SSMs提供了一种新颖的方法,以线性计算复杂度捕获长距离依赖关系,从而解决了Transformer固有的计算低效问题,同时保留了其全局上下文建模能力。U-Mamba [26]和VM-UNet [27]将Mamba模块引入到U-net结构中,以解决生物医药图像分割问题。为了促进通道间的信息流动,MambaMixer [16]引入了通道混合的Mamba模块到图像识别和时间序列预测中。然而,现有的U形Mamba架构并没有集成通道SSM模块,这对于在丰富的通道维度上下文中压缩和重建特征至关重要。在这项工作中,作者提出了一种高效且有效的双向Mamba U-Net,它在图像恢复过程中同时考虑了全局上下文和通道相关性。
Method
作者旨在开发一种有效的U-Net,该网络专注于图像修复中的长距离空间和通道相关性。作者提出了CU-Mamba模型,该模型应用空间和通道SSM块来学习全局上下文和通道特征,仅具有线性复杂性。在本节中,作者首先介绍U-Net设计的整体流程,然后通过解释以下内容深入探讨其组成部分:选择性的SSM框架、作者的空间SSM块以及作者的通道SSM块。最后,作者分析作者模型的计算成本以证明其效率。
Overall Pipeline
图1展示了CU-Mamba的整体框架。给定一个退化的图像 I ∈ R H × W × 3 I \in R^{H \times W \times 3} I∈RH×W×3,首先通过一个 3 × 3 3 \times 3 3×3 卷积来获取低级特征 X ∈ R H × W × C X \in R^{H \times W \times C} X∈RH×W×C。 X X X 然后被送入一个4级的对称编码器-解码器U-Net结构中,以形成细粒度、高质量的特征。在每一级 l l l,编码器包含 N N N 个CU-Mamba块和一个下采样层。具体来说,每个CU-Mamba块包含一个空间SSM块,后面跟着一个通道SSM块,如图1中的(⑴)和(2)所示。下采样操作逐级减少空间尺寸并增加通道数量,形成特征图 X ∈ R i × H 2 l × W 2 l × 2 C X \in R^{i \times \frac{H}{2^l} \times \frac{W}{2^l} \times 2C} X∈Ri×2lH×2lW×2C。
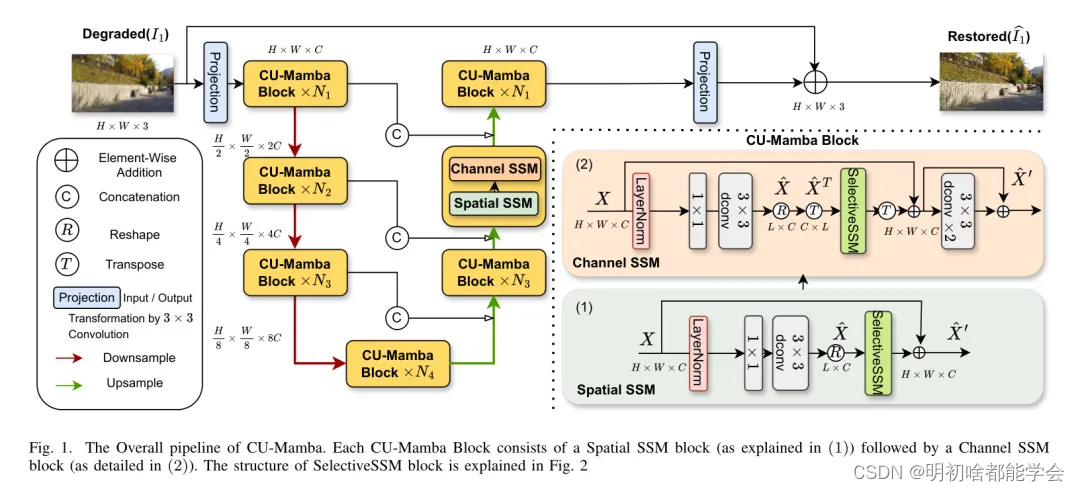
在公式中, i i i表示真实图像, F F F是傅里叶变换到频域的操作。在实验中,作者设置 ϵ = 1 0 − 3 \epsilon = 10^{-3} ϵ=10−3 和 λ = 0.1 \lambda = 0.1 λ=0.1。
Selective SSM Framework
作者提供了一个简单的概述,关于作者框架中所采用的的选择性SSM(Mamba)机制[13]。
结构化状态空间序列模型(SSMs)通过一个隐含的潜在状态 h ( t ) ∈ R N h(t) \in \mathbb{R}^N h(t)∈RN将一维序列输入 a ( t ) ∈ R a(t) \in \mathbb{R} a(t)∈R映射到 y ( t ) ∈ R y(t) \in \mathbb{R} y(t)∈R。一个SSM由四个参数 ( Δ , A , B , C ) (\Delta,A,B,C) (Δ,A,B,C)定义,具有以下操作:
h t = A h t − 1 + B a t y t = C h t \begin{align*} h_t &= Ah_{t-1} + Ba_t \\ y_t &= Ch_t \end{align*} htyt=Aht−1+Bat=Cht
在公式中, ( A , B ) (A,B) (A,B)是通过固定变换从 ( A , B ) (A,B) (A,B)得到的离散版本,即 A = f A ( Δ , A ) A = f_A(\Delta,A) A=fA(Δ,A)和 B = f B ( Δ , A , B ) B= f_B(\Delta,A,B) B=fB(Δ,A,B)。在SSM块中可以采用各种离散化规则,而离散化使得通过全局卷积的高效并行化训练成为可能。
尽管离散化带来了效率,但在SSMs中的参数 ( Δ , A , B , C ) (\Delta,A,B,C) (Δ,A,B,C)是数据独立的且时间不变的,这限制了隐藏状态在压缩已观察上下文时的表现力。选择性SSM (或Mamba)引入了数据相关参数 ( B , C , Δ ) (B,C,\Delta) (B,C,Δ),这些参数能有效选择$x_t $中的相关信息:
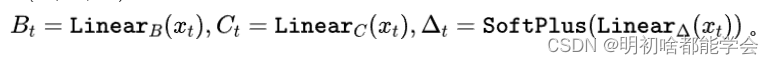
通过硬件感知优化,选择性的SSM(选择性状态空间模型)在与序列长度相关的计算和内存复杂性方面保持线性消耗,同时有效地压缩全局输入序列中的相关上下文。优化后的选择性SSM(Mamba)架构[13]如图2所示。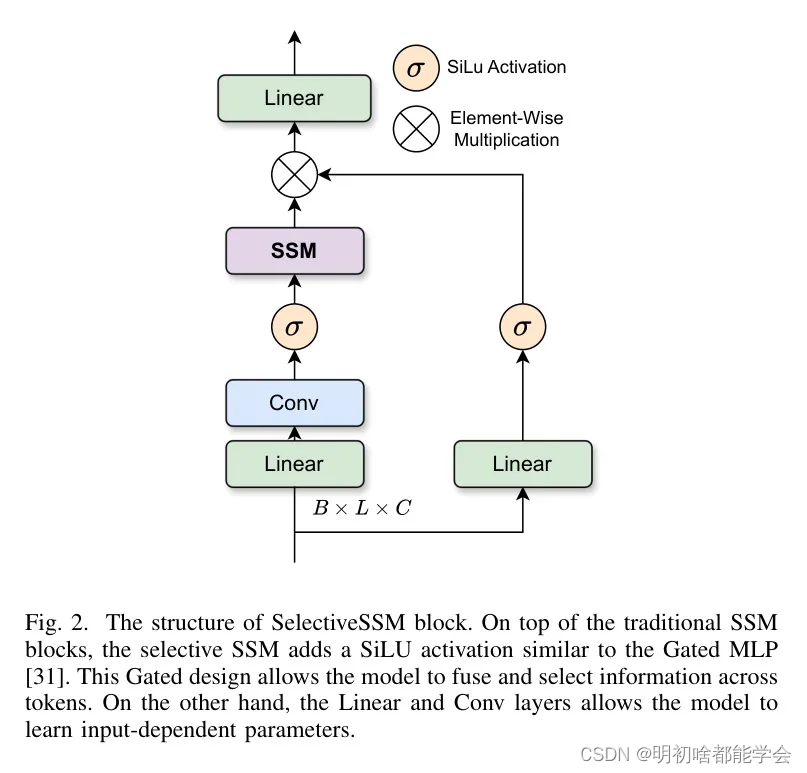
Global Learning Block: Spatial SSM
Transformer 架构的成功表明,通过U-Net的分层结构整合全局上下文对于高质量图像恢复至关重要。然而,这种全局感受野的代价是二次计算复杂度[20]。因此,作者设计了一个全局学习块,它有效地使用选择性的SSM框架压缩长距离上下文,这个框架只需要线性的计算复杂度。
给定一个层归一化的输入张量 X ∈ R H × W × C X \in R^{H \times W \times C} X∈RH×W×C,作者首先应用 1 × 1 1 \times 1 1×1 卷积在像素级别上聚合不同通道的上下文,然后使用 3 × 3 3 \times 3 3×3 深度卷积通过通道捕获空间上下文。接着,作者将特征图展平为 x ∈ R L × C x \in R^{L \times C} x∈RL×C,其中 L = H × W L = H \times W L=H×W,以构建特征块的序列。作者通过以下方式编码文的全局上下文:
selectivessN ( X ) \text{selectivessN}(X) selectivessN(X)
在图2中展示了选择性SSM块并对其进行了说明。作者可以将这一操作解释为从左上角到右下角线性扫描张量 X X X 的特征图,其中图中的每个像素都从所有先前看到的环境中学习其隐藏表示。最终的表示被Reshape为 X ∈ R H × W × C X \in R^{H \times W \times C} X∈RH×W×C,并在其 H × W H \times W H×W 维度内编码长距离依赖关系。
Channel Learning Block: Channel SSM
在U-Net架构中,下采样和上采样路径中的通道特征对于压缩和重建图像的上下文和结构至关重要。现有基于Mamba的U-Net的一个问题是,在扫描图像特征图以捕捉全局上下文时,通常忽略了通道信息。 为了学习跨通道特征之间的依赖关系,作者在通道维度上引入了选择性的SSM机制。
根据CSDN的规则,我将公式环境中的斜杠 “/” 替换为 “ " ,而公式单独一行显示时,则替换为 " ",而公式单独一行显示时,则替换为 " ",而公式单独一行显示时,则替换为"$”。下面是修复后的内容:
类似于空间SSM模块,给定一个层归一化的输入张量 X ∈ R H × W × C X \in R^{H \times W \times C} X∈RH×W×C,作者使用 1 × 1 1 \times 1 1×1 卷积后接 3 × 3 3 \times 3 3×3 深度卷积来预处理局部语境。然后,作者将 X X X转置为 X T ∈ R C × H × W X^T \in R^{C \times H \times W} XT∈RC×H×W并展平为$X_e \in R^{C \times 5} $。这可以被视为使用展平的特征像素作为通道表示。然后,作者通过以下方式应用选择性的SSM:
X ′ = selectivessM ( X T ) X' = \text{selectivessM}(X^T) X′=selectivessM(XT)
这个操作通过从上至下扫描通道图,有效地混合并记忆通道特征。最终的特征 X ′ X' X′被重新调整形状并转置回 X ∗ ∈ R H × W × C X^* \in R^{H \times W \times C} X∗∈RH×W×C。然后它被传递给带有LeakyReLU激活函数的2个 3 × 3 3 \times 3 3×3 深度卷积块,以平滑局部表示。
CU-Mamba的计算复杂度
作者遵循和的复杂性分析。将批量大小表示为 B B B,输入序列长度表示为 L L L(这里, L = H × W L = H \times W L=H×W),通道维度表示为 C C C,扩展因子表示为 E E E(在作者的实现中 E = 2 E=2 E=2)。采用高效的并行扫描算法,空间SSM块的计算复杂度为 O ( B L E + E C ′ ) O(BLE + EC') O(BLE+EC′),而通道SSM块的复杂度为 O ( B C E + E L ) O(BCE + EL) O(BCE+EL)。因此,总复杂度为 O ( B E ( L + C ) ) O(BE(L + C)) O(BE(L+C)),这在与序列长度和通道维度成线性关系。
这篇关于CU-Mamba:具有通道学习功能的选择性状态空间模型用于图像恢复的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






