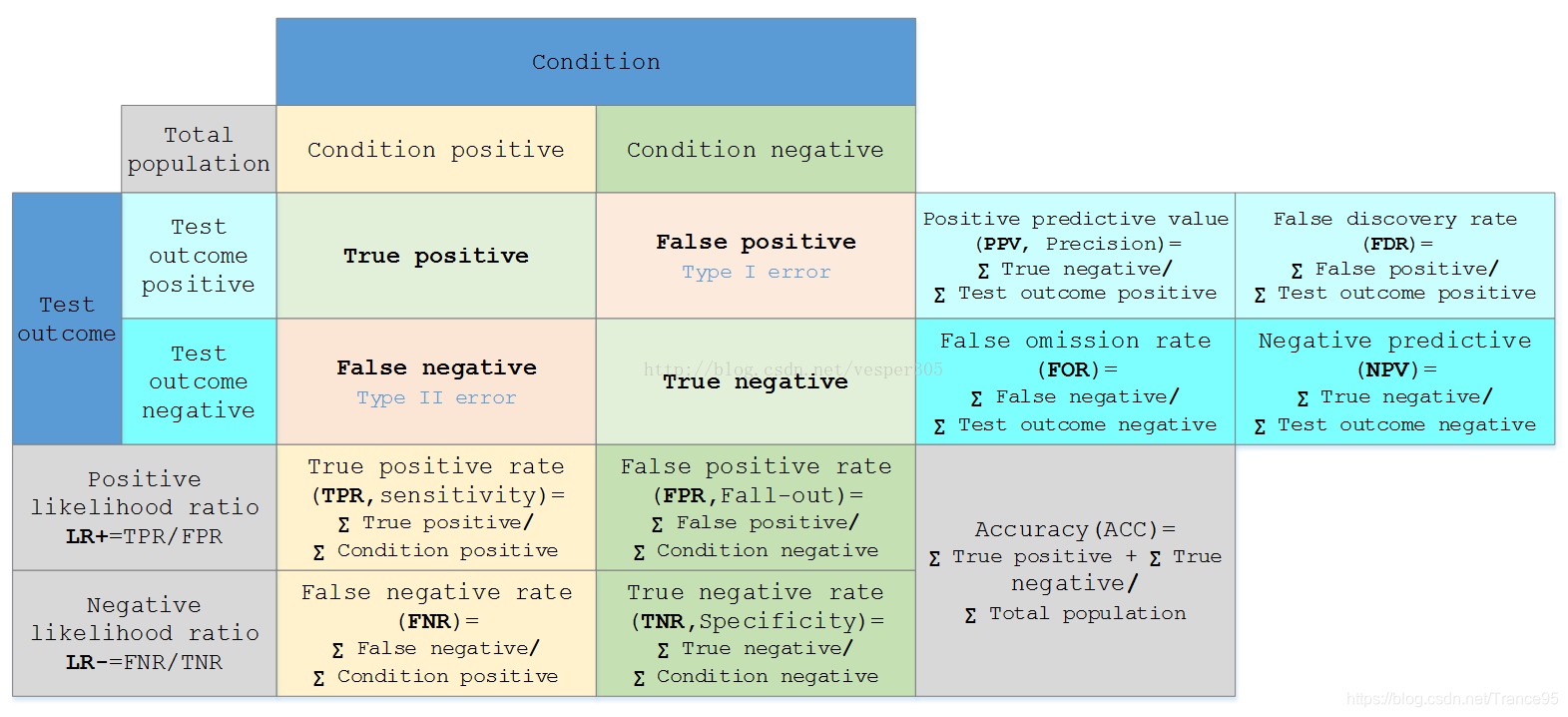
本文主要是介绍[机器学习] 第二章 模型评估与选择 1.ROC、AUC、Precision、Recall、F1_score,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
准确率(Accuracy) = (TP + TN) / 总样本 =(40 + 10)/100 = 50%。 定义是: 对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。
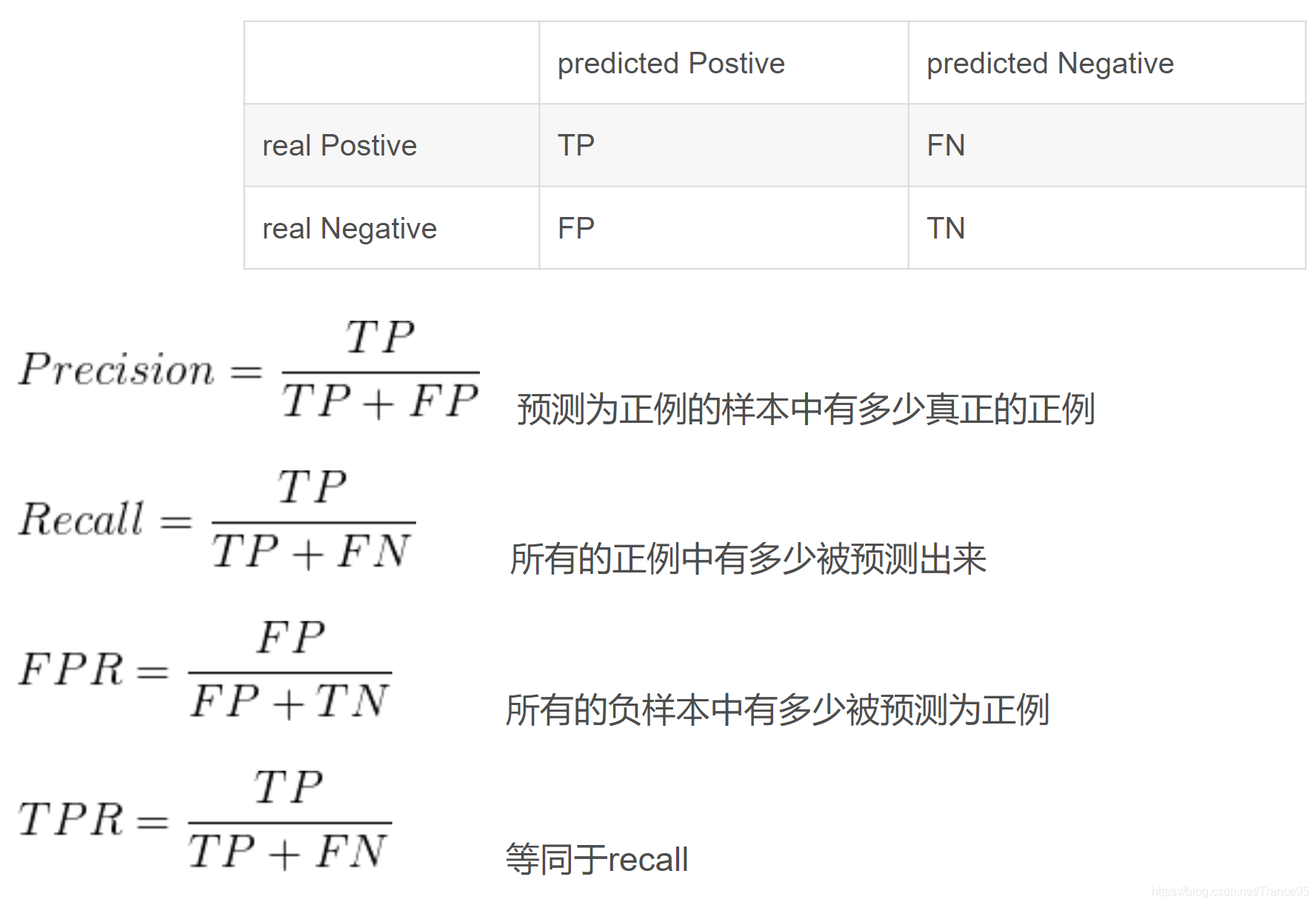
精确率(Precision) = TP / (TP + FP) = 40/60 = 66.67%。它表示:预测为正的样本中有多少是真正的正样本,它是针对我们预测结果而言的。Precision又称为查准率。
召回率(Recall) = TP / (TP + FN) = 40/70 = 57.14% 。它表示:样本中的正例有多少被预测正确了, 它是针对我们原来的样本而言的。Recall又称为【查全率】。
序列中的recall
原始输入 n_gram划分后,得到的个数 n=正例个数。
模型预测输出 n_gram划分后,
recall = 输出的词 ∩ 原始输入词 / 原始输入词
1.非均衡分类问题
类别分类代价不等
例如:垃圾邮件过滤中,我们希望重要的邮件永远不要被误判为垃圾邮件。
还有在癌症检测中,宁愿误判也不漏判。
此时分类错误率的度量不充分
所以,在分类中,当某个类别的重要性高于其他类别时,可以使用Precison和Recall多个比分类错误率更好的新指标。
条件阳性(P)
数据中真实阳性病例的数量
条件否(N)
数据中实际否定案例的数量
Precision(查准率): TP/ (TP+FP)
预测为正例的样本中真正正例的比例。
eg: 99正 1负 预测 1正√ 99负
TP/(TP+FP) 1/1
正例漏判为负例(垃圾邮件归为非垃圾邮件) 好于 负例误判为正例 (非垃圾邮件判为垃圾邮件)
Recall(召回率)(灵敏度)(TPR) : TP/P
真正为正例的样本有多少被预测出来。
eg: 99正 1负 预测 100正
负例误判为正例(没病也判有病) 好于 正例漏判为负例 (有病判没病)
TP/(TP+FN)= TP/P=sensitive P: 真实为阳性病例的数量
例如:在癌症检测中,我们希望选择Recall较高的模型(有病为正例)。
而在垃圾邮件过滤中,我们希望选择Precison较高的模型。
ROC (Receiver Operating Characteristic)
ROC是一个用于度量分类中的非均衡性的工具,ROC曲线及AUC常被用来评价一个二值分类器的优劣。
横坐标为 假阳率FP R(False positive rate )
纵坐标为 真阳率TP R(True postive rate)
ROC 描绘了两者的相对权衡:
benefits(TP) costs (FP)
FPR = FP/(FP+TN) 假阳率 = 假正例 / 负例
TPR = TP/ (TP+FN) = TP/P 真阳率 = 真正例 / 正例 (等同于recall)
接下来我们考虑ROC曲线中的四个点和一条线。
1.(0,0):fp=tp=0 ,即所有样本都被预测为负样本;
2.(1,1):fp=tp=1,所有样本都被预测为正样本;
3.(1,0):(x轴)fp=1,tp=0(y轴),所有正例都被预测为负例,而所有正例都没被预测出来,这时最糟糕的分类器,因为它成功的避开了所有正确答案。
4.(0,1):fp=0,tp=1,这是一个完美的分类器,它将所有样本都正确分类。
所以经过上述分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好,意味着分类器在假阳率很低的同时获得了很高的真阳率。
- 虚线y=x:这条对角线熵的点其实代表的是一个采用随机猜测策略的分类器的结果。例如(0.5,0.5),表示对于一半的样本猜测其为正样本,另外一半样本为负样本。出现在右下角三角形中的任何分类器都比随机猜测更糟糕。因此,在ROC图中,此三角形通常为空。
ROC曲线的横坐标和纵坐标其实是没有相关性的,所以不能把ROC曲线当做一个函数曲线来分析,应该把ROC曲线看成无数个点,
每个点都代表一个分类器,其横纵坐标表征了这个分类器的性能。为了更好的理解ROC曲线,我们先引入ROC空间,
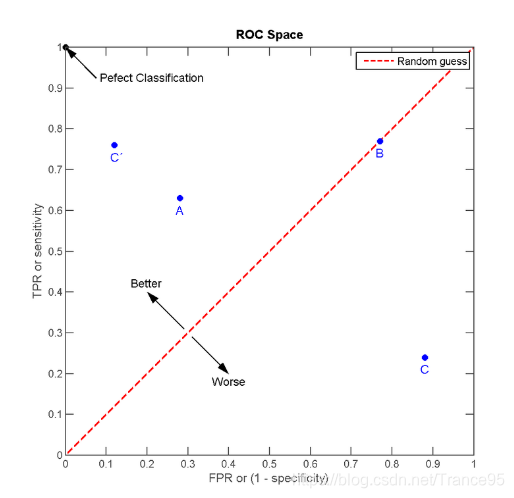
通过ROC空间,我们明白了一条ROC曲线其实代表了无数个分类器。
那么我们为什么常常用一条ROC曲线来描述一个分类器呢?
仔细观察ROC曲线,发现其都是上升的曲线(斜率大于0),且都通过点(0,0)和点(1,1)。
其实,这些点代表着一个分类器在不同阈值下的分类效果,具体的,曲线从左往右可以认为是阈值从0到1的变化过程。
当分类器阈值为0,代表不加以识别全部判断为0,此时TP=FP=0,TPR=TP/P=0,FPR=FP/N=0;
当分类器阈值为1,代表不加以识别全部判断为1,此时FN=TN=0,P=TP+FN=TP, TPR=TP/P=1,N=FP+TN=FP, FPR=FP/N=1。
所以,ROC曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。
对于ROC曲线,一个重要的特征是它的面积,面积为0.5为随机分类,识别能力为0,面积越接近于1识别能力越强,面积等于1为完全识别。
AUC (Area Under Curve)
AUC(Area Under Curve) 被定义为ROC曲线下的面积,
因为ROC曲线一般都处于y=x这条直线的上方,所以取值范围在0.5和1之间,
使用AUC作为评价指标 是 因为ROC曲线在很多时候并不能清晰地说明哪个分类器的效果更好,
而AUC作为一个数值,其值越大代表分类器效果更好。
首先AUC是一个概率值,当随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的分数将这个正样本排在负样本前面的概率就是AUC值。所以,AUC的值越大,当前的分类算法越有可能将正样本排在负样本值前面,既能够更好的分类。
ROC曲线的绘制
它代表的是分类器以多大的置信度将样本分类为正样本。分类器的一个重要功能”概率输出“,即表示分类器认为某个样本具有多大的概率属于正样本(或负样本)。
假设我们已经得到了所有样本的概率输出(即属于正样本的概率),那么我们就可以通过改变”discrimination threshold“来绘制ROC曲线。
(分类器得到样本的判别为正的概率,然后设置阈值,大于阈值为正)
当使用这样的离散分类器时,产生一个单个confusion矩阵(混淆矩阵),对应于一个ROC点。
而一些分类器,例如Naive Bayes,产生一个样本概率值,这样一个ranking/scoring分类器可以使用一个threshold来产生一个discrete(binary)分类器:
如果分类器输出的概率大于threshold,分类器产生Y,否则产生N。
每个不同的threshold值在ROC空间产生一个不同的点(对应于一个不同的confusion matrix)。
Confusion Matrix (混淆矩阵)
监督学习 :混淆矩阵 (Confusion Matrix)
非监督学习:匹配矩阵(Matching Matrix)
行:实际的类别
列:预测值
这个名字来源于它可以非常容易的表明多个类别是否有混淆(也就是一个class被预测成另一个class)。
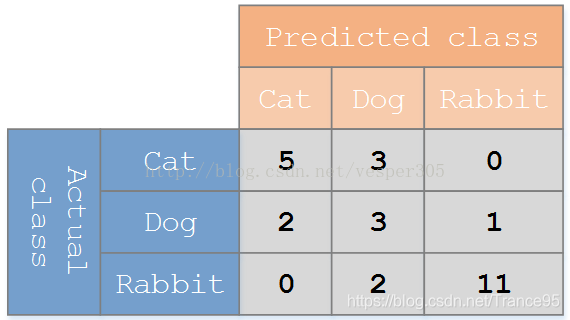
准确率对于分类器的性能分析来说,并不是一个很好地衡量指标,因为如果数据集不平衡(每一类的数据样本数量相差太大),很可能会出现误导性的结果。例如,如果在一个数据集中有95只猫,但是只有5条狗,那么某些分类器很可能偏向于将所有的样本预测成猫。整体准确率为95%,但是实际上该分类器对猫的识别率是100%,而对狗的识别率是0%。
猫类别的混淆表格如下:
F1 score
precision 和 recall 调和平均数
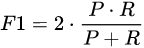
准确率(Accuracy)
准确率(accuracy)计算公式为:
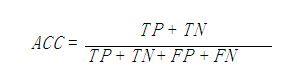
灵敏度(sensitive)
sensitive = TP/P,表示的是所有预测为正例中被分对的比例,衡量了分类器对正例的识别能力。
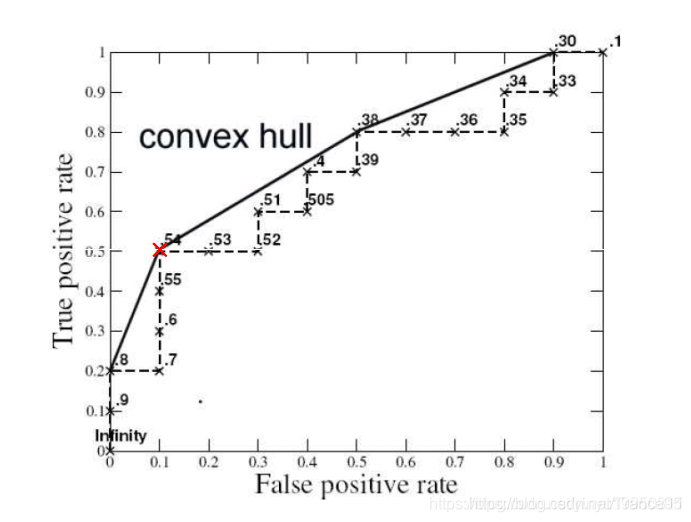
Convex Hull
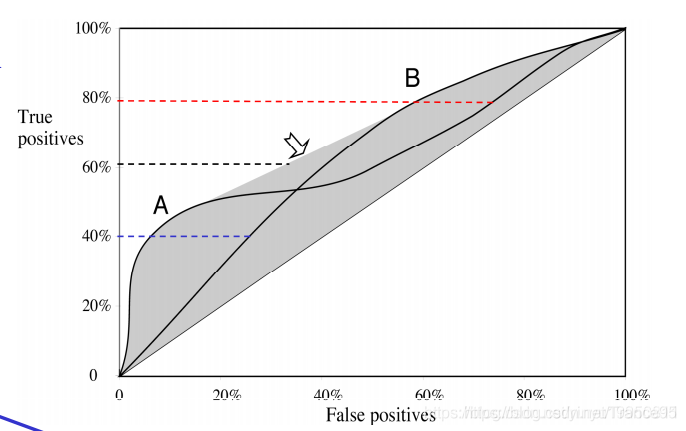
阴影区域被称作两个曲线的convex hull。
在选择分类器时总是应该根据convex hull的上边界进行操作。
e.g.:
如果你的目标是覆盖40%的真阳性,你应该选择方法A,这样可以提供5%的更低的假阳性率
如果你的目标是覆盖80%的真阳性,你应该选择方法B,因为B的假阳性率为60%,与A相比更低。
如果你的目标是覆盖60%的真阳性,那么你应该结合A和B。
准确性的不足(代价敏感学习)
将样本误分类为正样本 和 将样本误分类为负样本的代价是不同的。
分类代价 相比 分类准确率具有更加重要的意义。
传统的分类算法不适合解决代价敏感的问题,所以在传统分类方法中引入 代价因子,运用代价敏感学习减少分类代价。
成本矩阵Cost(i,j) :表示将 i 类样本误分类为类 j 的代价。
代价敏感分类 就是为不同类型的错误分类不同的代价,使得分类时,高代价错误产生的数量 和 错误分类的代价总和最小。
MetaCost(代价敏感学习):MetaCost是一种典型的 集成学习算法,其核心思想是计算出每个训练样本预测分类概率,再根据最优分类期望代价重标记原训练样本的类标号,得到新的训练集,然后在新的训练集上重新运行目标分类算法进行训练,从而实现代价敏感分类。
ROC曲线的python代码实现
# 关于iris数据集
# 鸢尾花(Iris)数据集: 3类共150条记录,每个记录有4个特征。通过4个特征预测3分类。
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
#sklearn.svm将被弃用,移动到.multiclass 多分类模块中
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc ###计算roc和auc
#from sklearn import cross_validation ##这个将被弃用,被移动在model_selection模块内
from sklearn.model_selection import train_test_split
# ovr(一对多): 多分类问题
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import label_binarizefrom itertools import cycle
#from scipy import interp (interp被移动到np.interp)
from sklearn.metrics import roc_auc_scoreiris = datasets.load_iris()
X = iris.data
y = iris.target#二分类
# y = label_binarize(y,classes=[0,1])
# n_classes = y.shape[1]# 对于多分类,二值化标签
# Binarize the output
y = label_binarize(y,classes=[0,1,2])
n_classes = y.shape[1]random_state = np.random.RandomState(0)
n_samples,n_features = X.shape
X = np.c_[X,random_state.randn(n_samples,200*n_features)]
# shuffle and split training and test sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size =.3,random_state=0)
#X_train,X_test,y_train,y_test = cross_validation.train_test_split(X,y,test_size=.3,random_state=0)# #定义分类器
# classifier = svm.SVC(kernel='linear',probability=True,random_state=random_state)
# # 测试集Y_test的打分
# # y_score = classifier.fit(X_train,y_train).decision_function(X_test)classifier = OneVsRestClassifier(svm.SVC(kernel='linear',probability=True,random_state=random_state))
y_score = classifier.fit(X_train,y_train).decision_function(X_test)# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
# iris是3类
n_classes = len(y_test[0])
for i in range(n_classes):# 第i类的fpr和tpr和aucfpr[i],tpr[i],_ = roc_curve(y_test[:,i],y_score[:,i])roc_auc[i] = auc(fpr[i],tpr[i])# Compute micro-average ROC curve and ROC area
# ravel 化成水平
fpr["micro"],tpr["micro"],_= roc_curve(y_test.ravel(),y_score.ravel())
roc_auc['micro'] = auc(fpr['micro'],tpr['micro'])
#------------------二分类roc------------------
# 二分类,第2类的roc曲线和面积(第一类0.95,第二类0.6)
plt.figure()
lw = 2
# fpr[i],tpr[i],roc_auc[i]
plt.plot(fpr[1], tpr[1], color='darkorange',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[1])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
#------------------多分类roc------------------
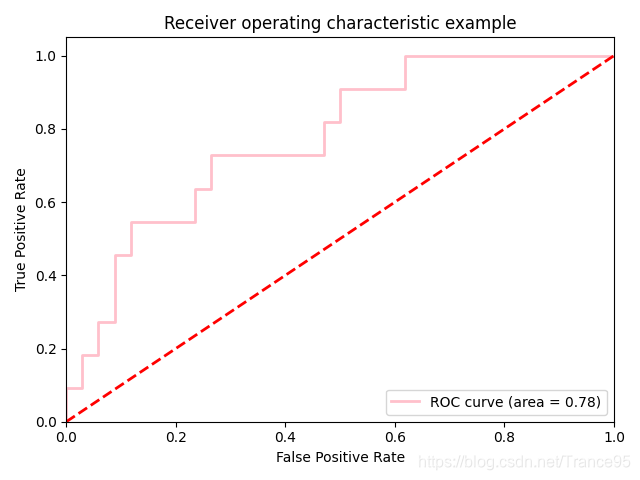
# 多分类,第3类的roc曲线和面积(第一类0.95,第二类0.6,第三类0.78)
plt.figure()
# 线的粗细>0
lw = 2
plt.plot(fpr[2], tpr[2], color='pink',lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='red', lw=lw, linestyle='--')
#plt.plot(fpr[2], tpr[2], color='darkorange',
# lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
# plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
# xlim,ylim x和y的范围
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()# ------------------------------绘制多标签问题的ROC曲线(计算宏观平均roc和aoc面积)
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):# interp 被移动到np.interpmean_tpr += np.interp(all_fpr, fpr[i], tpr[i])# Finally average it and compute AUC
mean_tpr /= n_classesfpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])# Plot all ROC curves
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],label='micro-average ROC curve (area = {0:0.2f})'''.format(roc_auc["micro"]),color='deeppink', linestyle=':', linewidth=4)plt.plot(fpr["macro"], tpr["macro"],label='macro-average ROC curve (area = {0:0.2f})'''.format(roc_auc["macro"]),color='navy', linestyle=':', linewidth=4)colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):plt.plot(fpr[i], tpr[i], color=color, lw=lw,label='ROC curve of class {0} (area = {1:0.2f})'''.format(i, roc_auc[i]))plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()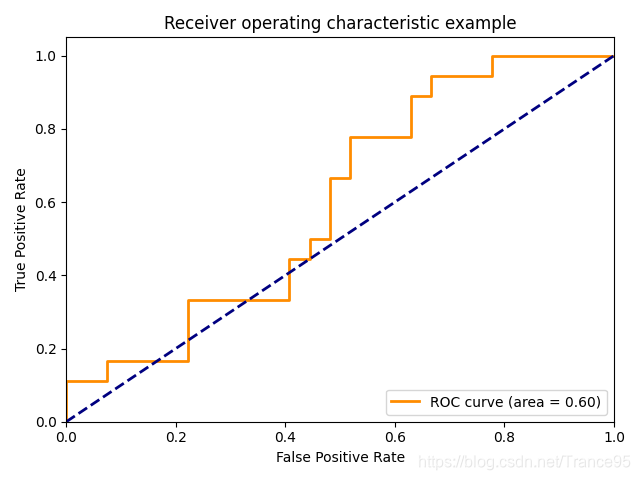

关于 roc_curve源代码详解 参见另一篇博客 https://editor.csdn.net/md/?articleId=116424439
参考:https://zhuanlan.zhihu.com/p/26293316
参考:https://blog.csdn.net/yinyu19950811/article/details/81288287
参考:https://blog.csdn.net/vesper305/article/details/44927047
代码见官方文档:https://scikit-learn.org/stable/auto_examples/model_selection/plot_roc.html
这篇关于[机器学习] 第二章 模型评估与选择 1.ROC、AUC、Precision、Recall、F1_score的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








