本文主要是介绍R数据分析:一般线性回归的做法和解释,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
发现大家做分析做的最多的还是线性回归,很多人咨询的都是线性回归的问题,今天专门出一个线性回归的文章。
在R语言中我们可以非常方便地用基础包中的lm方法做出线性回归。参数的书写也和数学方程一样一样的Y~X+X2,只不过将等号换成了~。我们用summary+回归对象就可以得到回归结果,如果要看模型的残差直接$resid就可以。
还是给大家写一个活生生的例子吧:
实例描述:
我们有如图的数据集,我想要用回归分析做month, spend对sales的关系。

首先读入数据集(请私信“数据链接”获取)并且规定数据属性:
dataset = read.csv("data-marketing-budget-12mo.csv", header=T,
colClasses = c("numeric", "numeric", "numeric"))简单线性回归和多元线性回归
在我们的例子中,因变量是sales,如果我只用一个自变量,比如spend来做预测,此时就是简单线性回归;如果我用两个或者两个以上的自变量来做预测就是多元线性回归,做法都很简单:
simple.fit = lm(Sales~Spend, data=dataset)
summary(simple.fit)
multi.fit = lm(Sales~Spend+Month, data=dataset)
summary(multi.fit)两个模型的输出都给大家贴在下面:

对于模型,首先我们应该看整个模型的显著性,也就是模型的F检验,可以看到两个模型都有意义,然后我们再看R方和调整的R方,可以看到我们的模型贼好,然后我们再看每个变量的显著性。
输出结果的解释
首先有一个residuals:
- Residuals: The section summarizes the residuals, the error between the prediction of the model and the actual results. Smaller residuals are better.
这个是模型的残差,就是模型预测值和实际值之间的差异,应该是越小越好。
接着就是coefficients:
- Coefficients: For each variable and the intercept, a weight is produced and that weight has other attributes like the standard error, a t-test value and significance.
这个是模型中自变量的系数,这个系数又包含4个部分,分别是estimate,std,t和p
- Estimate: This is the weight given to the variable. In the simple regression case (one variable plus the intercept), for every one dollar increase in Spend, the model predicts an increase of $10.6222.
estimate解释为相应的自变量改变一个单位,应变量的改变量。Std. Error为它的标准误,t value为检验系数显著性的t统计量,Pr(>|t|)为p值,通过Pr(>|t|)我们可以知道该系数是不是显著地不等于0。
还有模型整体表现的指标:
- Residual Standard Error: This is the standard deviation of the residuals. Smaller is better.
这个是残差的变异,越小越好。
- Multiple / Adjusted R-Square: For one variable, the distinction doesn’t really matter. R-squared shows the amount of variance explained by the model. Adjusted R-Square takes into account the number of variables and is most useful for multiple-regression.
然后是R方和调整的R方,R方为这个模型能解释的变异比例,调整的R方考虑了自变量个数。如果我们做简单线性回归的话R方和调整的R方就是一样的。
还有模型表现的F-Statistic:
- F-Statistic: The F-test checks if at least one variable’s weight is significantly different than zero. This is a global test to help asses a model. If the p-value is not significant (e.g. greater than 0.05) than your model is essentially not doing anything.
F统计量是来看整个模型是不是有意义的,如果模型整体没意义相应的别的系数也就不用看了。
残差相关知识
对于线性模型我们有四个假设:
- The mean of the errors is zero (and the sum of the errors is zero)(线性)
- The distribution of the errors are normal.(正态)
- All of the errors are independent.(独立)
- Variance of errors is constant (Homoscedastic)(方差齐)
我们的模型满不满足这4个假设呢?我先画图看看:
layout(matrix(c(1,1,2,3),2,2,byrow=T))plot(simple.fit$resid~dataset$Spend[order(dataset$Spend)],main=" 简单线性回归的自变量和残差变化",xlab="Marketing Spend", ylab="Residuals")
abline(h=0,lty=2)hist(simple.fit$resid, main="残差的直方图",ylab="Residuals")qqnorm(simple.fit$resid)
qqline(simple.fit$resid)
残差是否正态?
我们可以从两个图中来判断残差是否正态:
- If the histogram looks like a bell-curve it might be normally distributed.
- If the QQ-plot has the vast majority of points on or very near the line, the residuals may be normally distributed.
首先是直方图,直方图是近似钟形的就为正态,QQ图中的点都和线靠得近就为正态。
但是我们数据量太少,看图似乎看不出来,我们考虑做个统计检验:
library(fBasics)
jarqueberaTest(simple.fit$resid)
检验结果告诉我们残差确实是正态的。
残差是否独立?
残差独立的意思就是残差之间不存在相关性,我们也需要做统计检验:
library(lmtest) #dwtest
dwtest(simple.fit)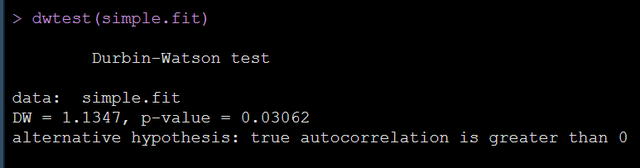
检验结果告诉我们残差的自相关很大。
残差是否齐?
对于这个假设,通常情况下我们也是看残差图,如果残差图没有明显的离群值我们就可以认为残差是齐的。
这篇关于R数据分析:一般线性回归的做法和解释的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








