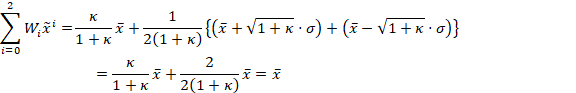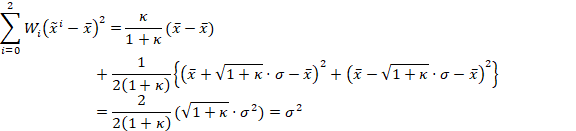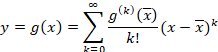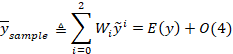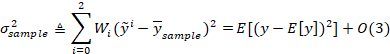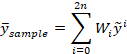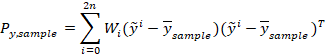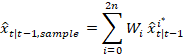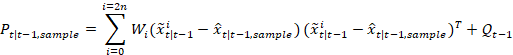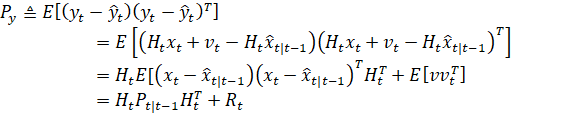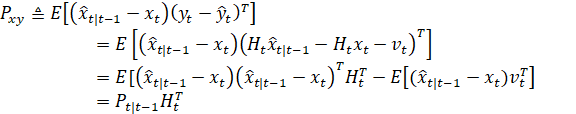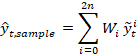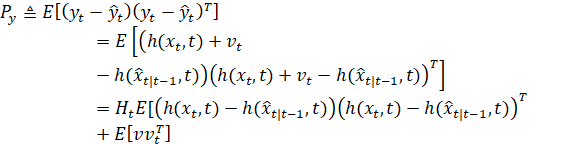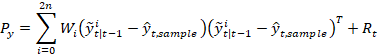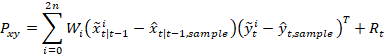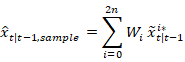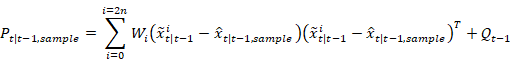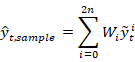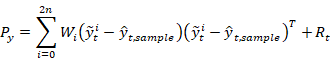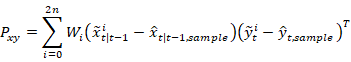无迹卡尔曼滤波（UKF）推导

本文主要是介绍无迹卡尔曼滤波（UKF）推导，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

pdf和图片链接：

链接：https://pan.baidu.com/s/1q8tIy1q5gqlhYEKH1l8frg 
提取码：yyds

1.1概述

无迹卡尔曼滤波(Unscented Kalman Filter),最初由Julier和Uhlmann提出，使用了一种不同的方法来计算误差协方差矩阵。它不使用(连续时间)黎卡提方程(Riccati Equations,形如、 的一类非线性方程)或(离散时间)协方差传播和更新规律。关键的思想是基于一组特殊的样本点来估计误差协方差，这些点被称为 点(Sigma Points)，这些点直接通过原始非线性模型传播。

1.2 无迹变换

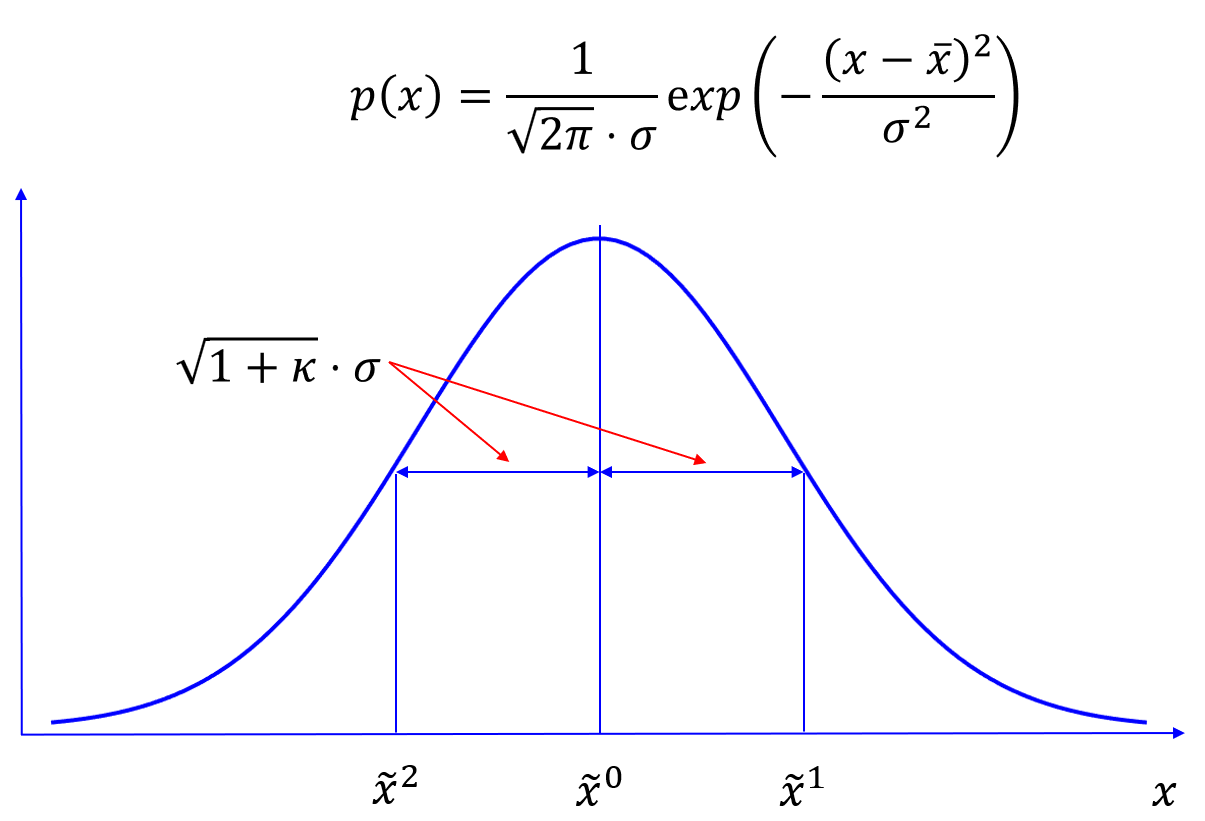
以一维高斯分布为例，随机变量为X，其中高斯分布的数学表达式为:

其中均值为 ，方差为 ，其分布函数如图1所示:

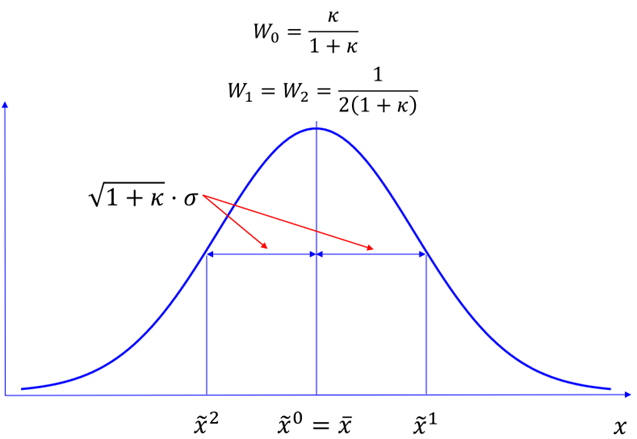
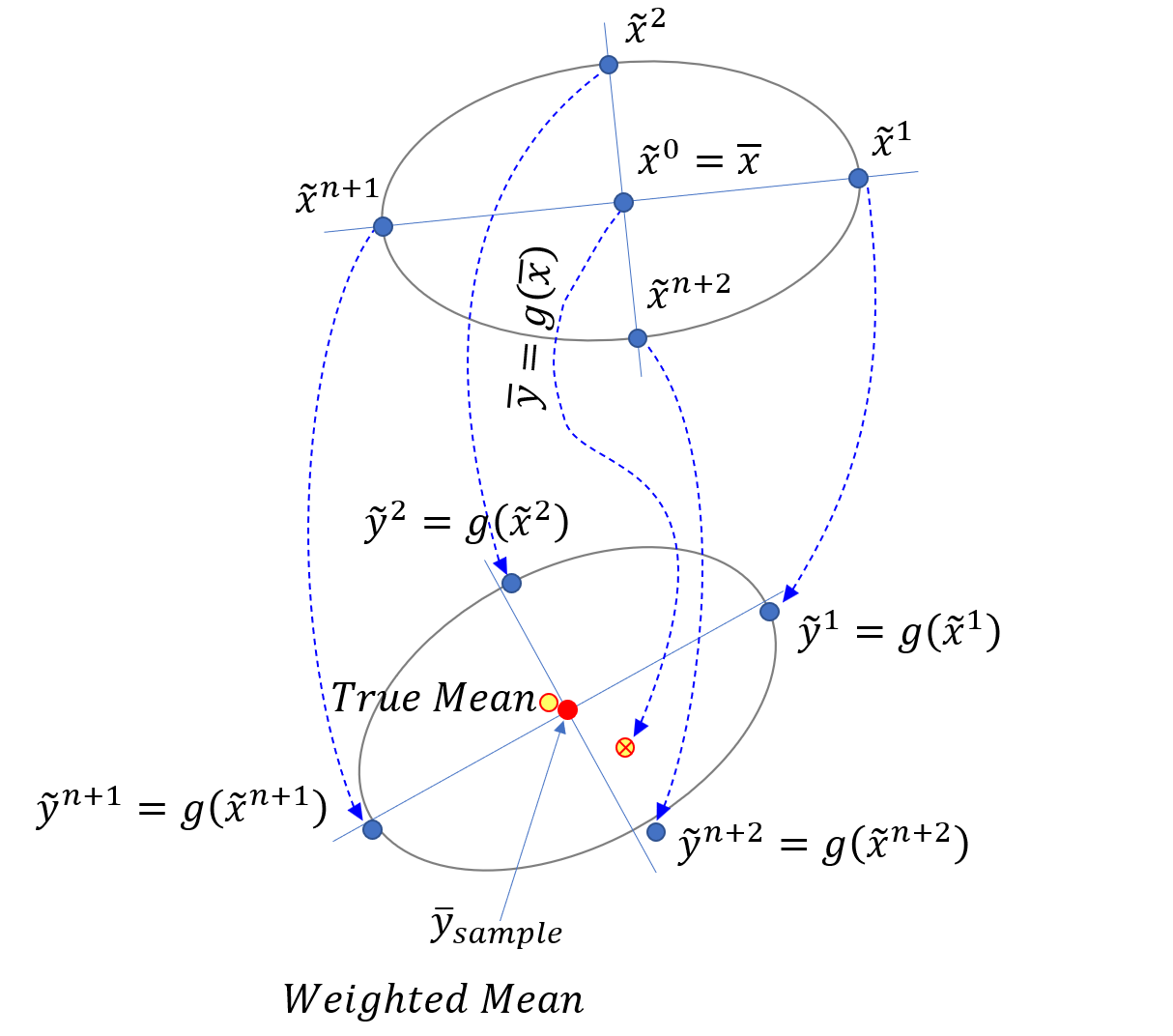
无迹变换表示有三个特殊样本点的高斯分布，称为 点，三个点分别为:

             

        

        

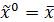
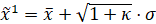
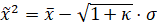
其中， 是需要调整的 点的参数， 是用于计算均值和方差的第 个 点的权值。

通过计算三个 点的加权均值，得出三个 点的加权均值与高斯分布的真实均值一致:

通过计算三个 点的加权方差，三个 点的加权方差与方差的真实值一致:

因此， 点的均值和方差提供了任意参数 值的真实高斯分布的正确均值和方差。

如图所示，现在有一个从x到y的非线性变换:

其中函数 是解析函数。

y的分布不再是高斯分布，但其均值 和方差 可以表征该分布。

我们可以证明通过非线性函数变换后的加权均值可以逼近三阶的真实均值。

其中 是一个4阶以上的小量。

进一步，我们可以证明加权方差可以近似真实方差到二阶。

1.3例子

如图所示，有 的分段线函数(为了可微性，两条线用光滑曲线连接)。

x的均值变换为 ，这并不是y分布的真实均值，通过检验我们可以看到:

点的加权平均值可以给出较好的平均值:

                                                                   

1.4 多元高斯分布的 点

1) 一般来说，对于n维高斯分布，我们使用2n+1个 点。

注意协方差矩阵 是实数、对称和正定的。因此，它可以对角化。

其中

2) 点沿单位长度的单个特征向量取 .

 

                    

          

         

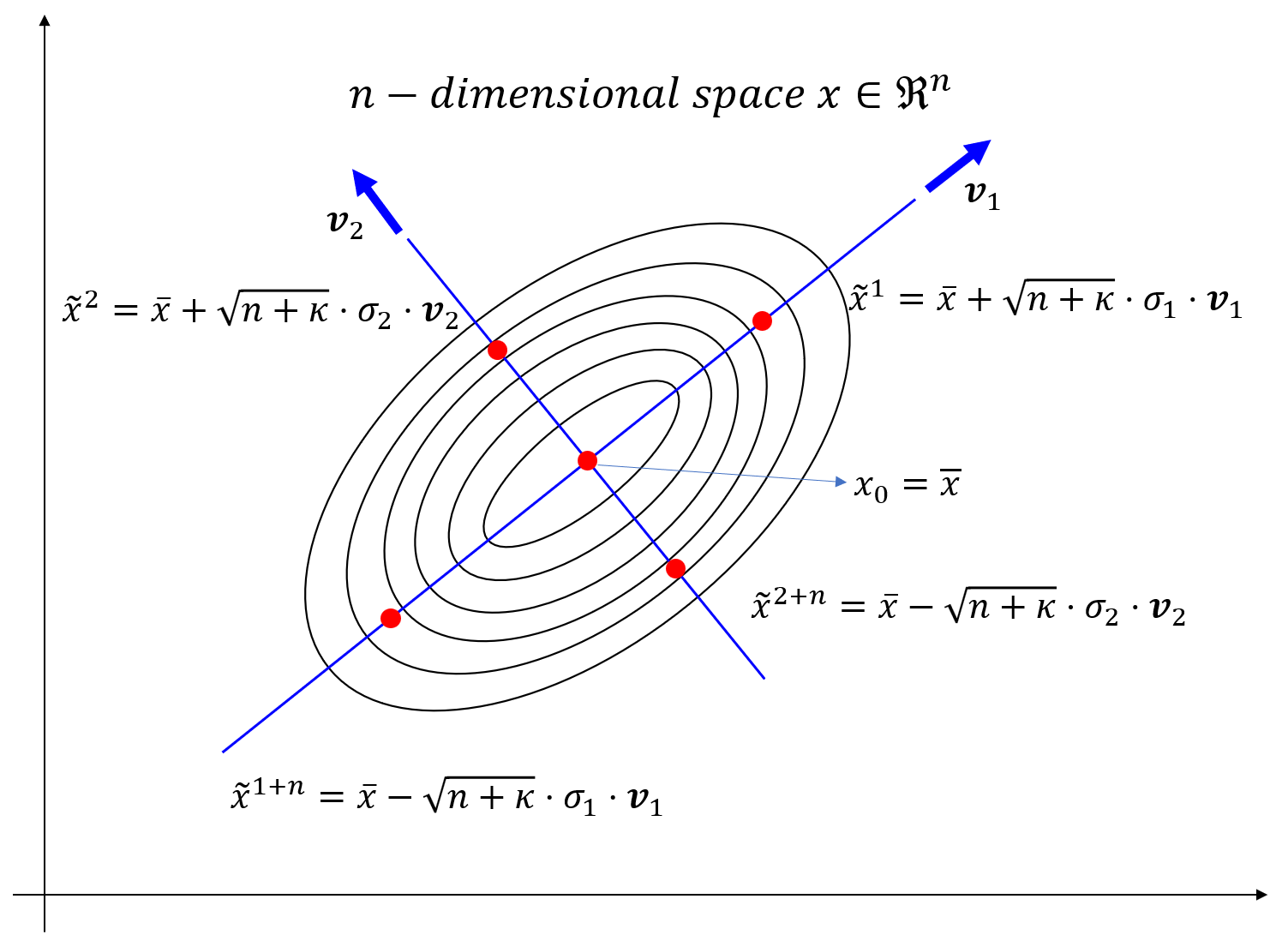
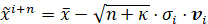
3) 和以前一样，所有的 点通过一个非线性解析函数传播， ，属于多元函数。

4) 对于这些传播点，计算加权平均值:

加权协方差为:

我们可以证明加权均值可以近似三阶真实均值，加权协方差可以近似二阶真实均值。这种采样方法称为无迹变换。

1.5无迹卡尔曼滤波

考虑一个非线性离散时间动态系统:

  

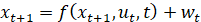
在不丢失一般性的情况下，我们将u设置为零， 。

过程噪声和测量噪声是零均值、不相关(白)噪声，协方差为 和 。

  

在时刻t-1，后验估计 和后验误差协方差是可用的:

问题是使用无迹变换找到递归公式:

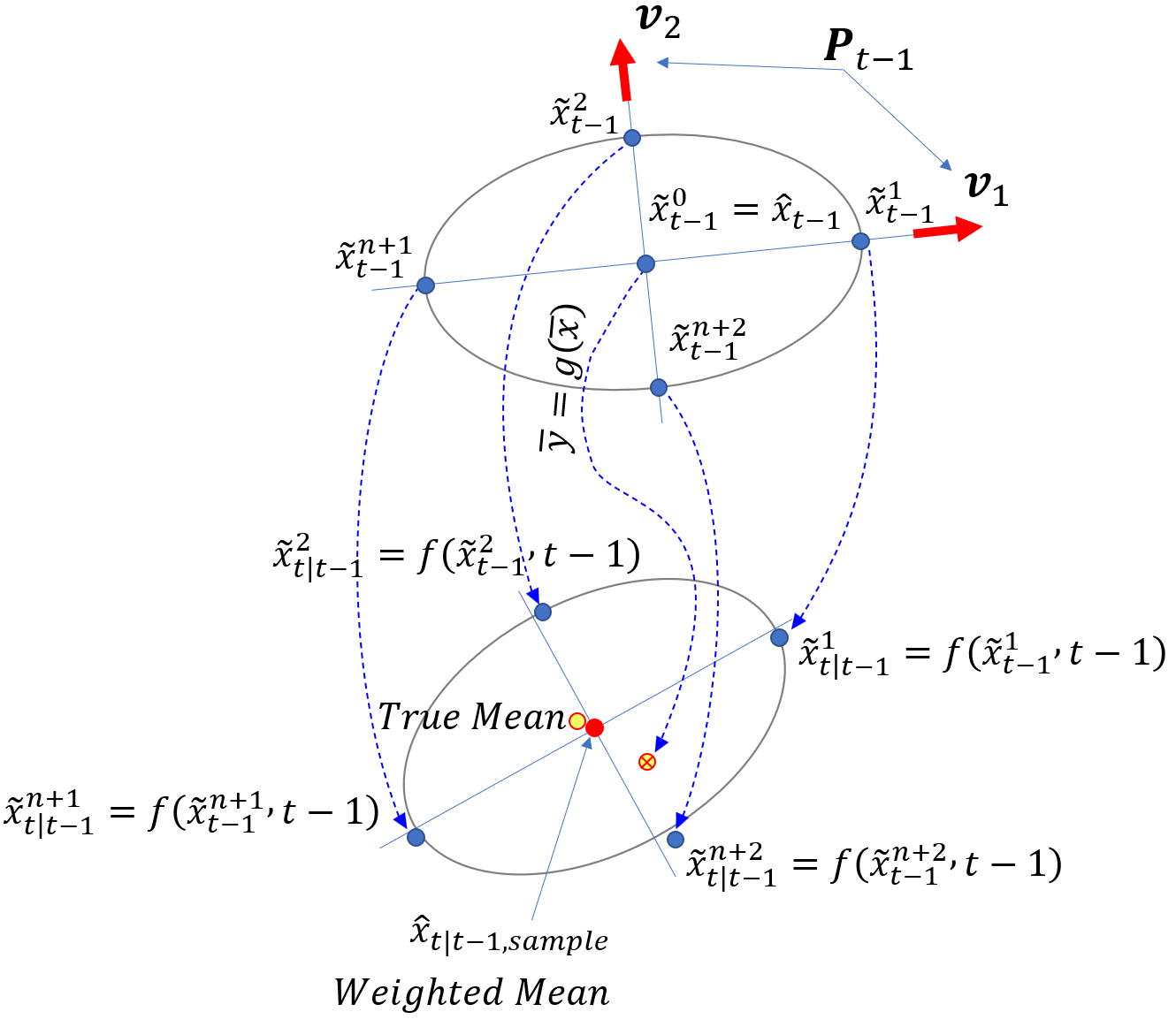
1)状态和协方差的传播:从 和 中求 和 ;

2)状态和协方差的更新:从 和 中找到 和 。

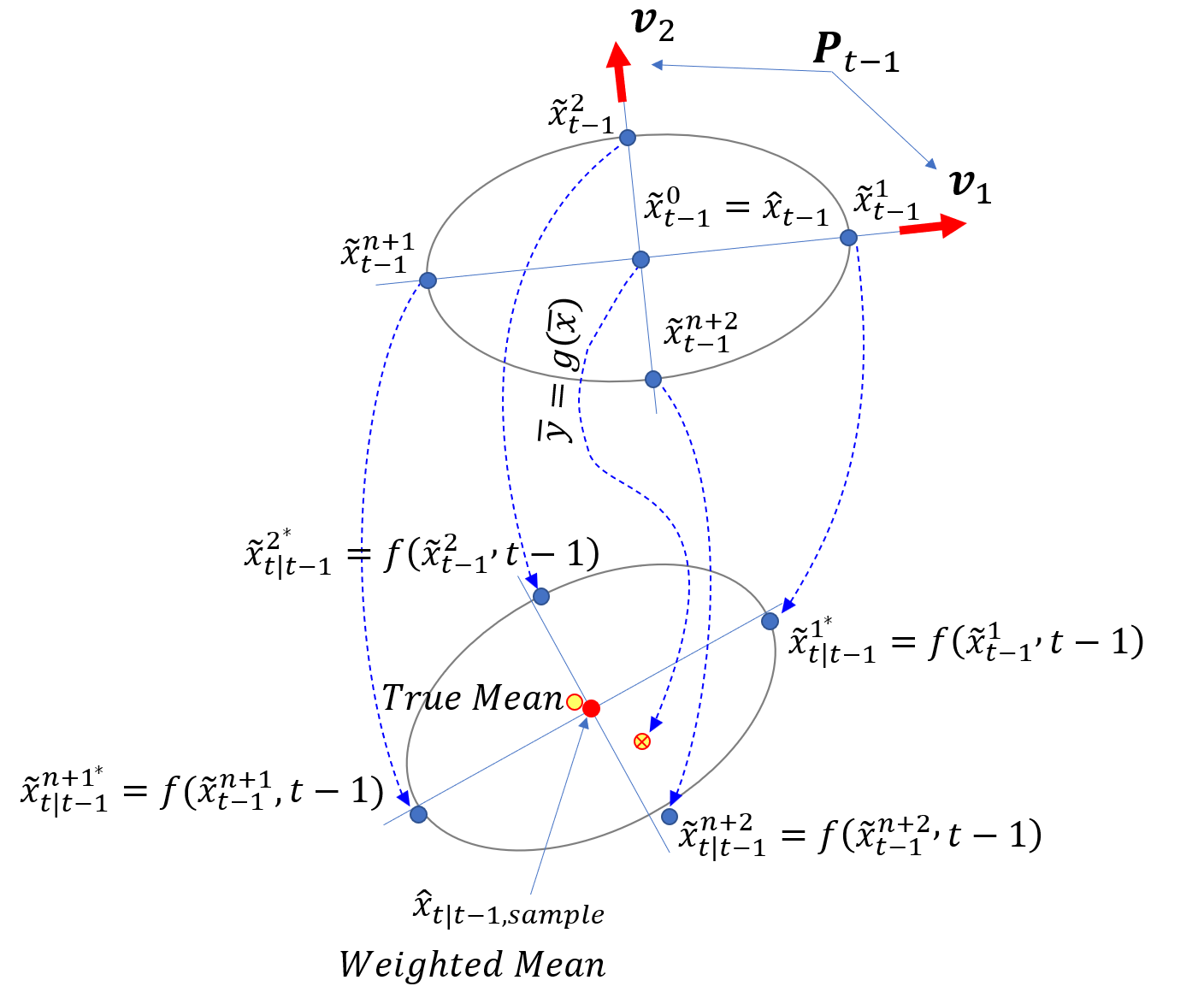
1.6 状态传播

1) 找到协方差 的特征值和特征向量，生成2n+1个点;

2) 通过状态方程传播 点，注意过程噪声为零均值:

3) 对于这些2n+1个 点，计算加权平均值:

1.7 协方差传播

先验协方差计算为:

 

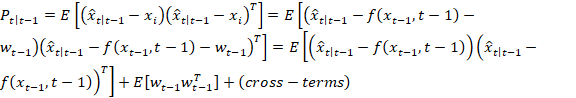
是未知的因为我们不知道 的确切状态。但是，加权平均值 近似于三阶。因此，我们将 替换为加权均值，并使用2n+1个 点计算先验协方差。

注意，预测的协方差在二阶前是正确的。为简便起见，下标“sample”将在下文中省略。

1.8利用新的协方差获得卡尔曼增益

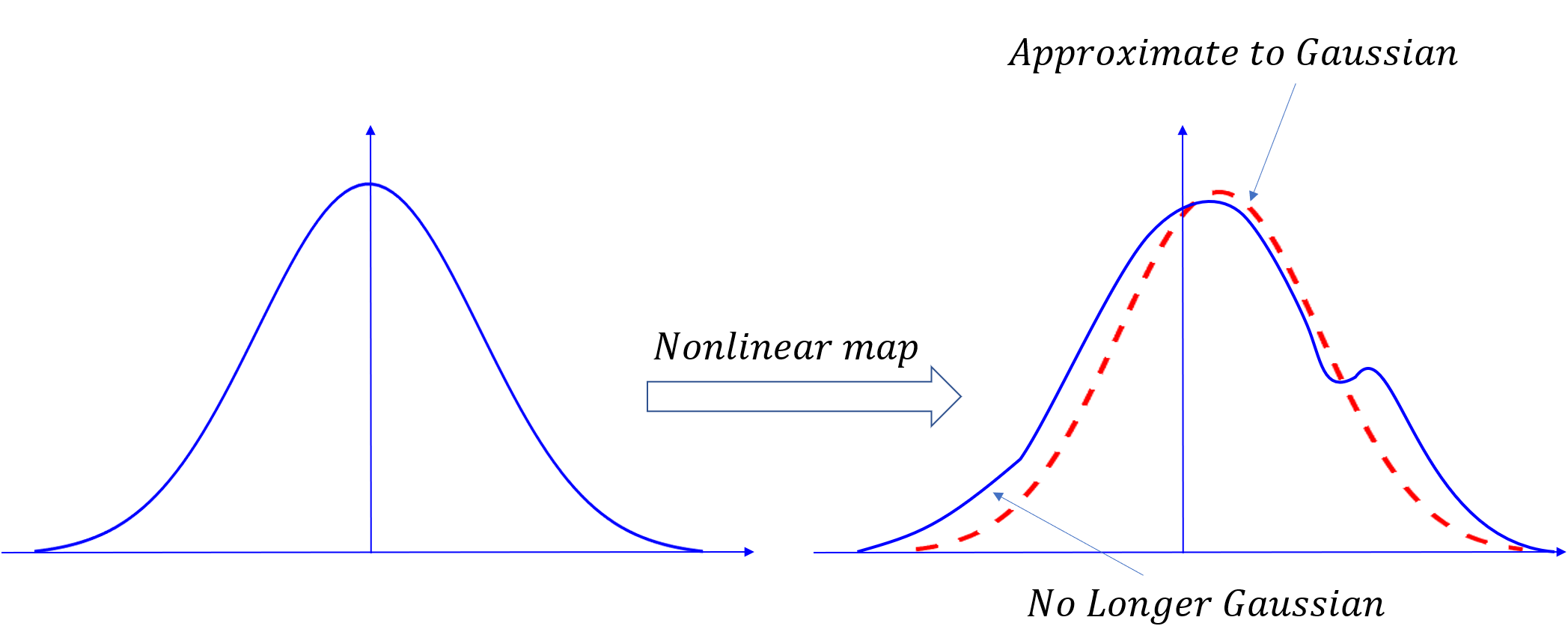
我们的目标是使用 点更新状态和协方差。然而，标准卡尔曼增益和协方差更新法不适用于无迹变换。相反，我们将考虑一种新的替代方法。卡尔曼增益为 ，但 矩阵对我们的非线性系统是不可用的。相反，我们使用下面的公式，

对于一个线性时变系统，这个新公式可以用结构证明。

结合上述两点，证明了卡尔曼增益的新公式。输出y的协方差称为“创新协方差”。

1.9 状态更新

通过对先验协方差 应用无迹变换可以更新状态和协方差。

1) 通过检验通过测量方程产生的输出，并通过分布来获得新协方差;

2) 计算先验协方差的特征值和特征向量:

3) 然后生成2n+1个 点，并估计输出y的分布与 点的均值和协方差；

4) 利用测量函数的确定性部分，将 点映射到:

5) 点的加权均值:

6) 结合创新协方差得到:

7) 用 点计算第一项:

同理，交叉协方差由:

8) 卡尔曼增益是 。

9) 状态更新为:

1.10协方差更新

1) 协方差更新公式中包含测量矩阵 ，需要替换。

我们可以使用创新协方差:

2) 协方差更新公式中插入协方差更新公式中插入 :

式中，利用卡尔曼增益消去测量矩阵 。

3) 利用 点，可以这样计算：

1.11无迹卡尔曼滤波器的递归算法

1) 给定 和 ，通过计算 的特征值和向量对 点进行抽样;

2) 将 点通过非线性模型传播得到 ;

3) 用2n+1个 点计算均值和方差:

4) 对 再次采样2n+1个 点;

5) 根据非线性测量方程，将传播的 点变换为输出估计 ，并计算输出估计:

6) 利用2n+1个点的传播输出估计来评估创新协方差和交叉协方差，得到卡尔曼增益:

7) 用卡尔曼增益更新状态估计:

8) 更新后验协方差:

9) 设 ，重复上述过程。

不需要雅可比矩阵，不需要偏导。用标准差点估计协方差比用雅可比矩阵估计协方差更精确。

警告!随机变量通过非线性方程 ， 变换后的分布不再是高斯分布，虽然原来的分布是高斯分布。

无迹卡尔曼滤波器将此分布近似为高斯分布，并以均值和协方差为特征。虽然该近似值精确到2阶，但随着过程的重复，与完全高斯分布的差异可能会增大。

这篇关于无迹卡尔曼滤波（UKF）推导的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---