本文主要是介绍二叉堆 | 大根堆 小根堆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
何为二叉堆
二叉堆的调整
最大堆
最大堆的插入操作
最大堆的删除操作
最大堆的构建
最大堆code
最小堆
小根堆的插入操作
最小堆的删除操作
最小堆的构建
最小堆code
二叉堆的存储方式
何为二叉堆
二叉堆本质上是一种完全二叉树,它分为两个类型:
- 最大堆
- 最小堆
二叉堆的调整
对于二叉堆,如下有几种操作:
- 插入节点:无论是大根堆还是小根堆,插入节点都是从完全二叉树的最后一个位置进行的,插入后再自下向上的调整,这一过程被称为“上浮”。
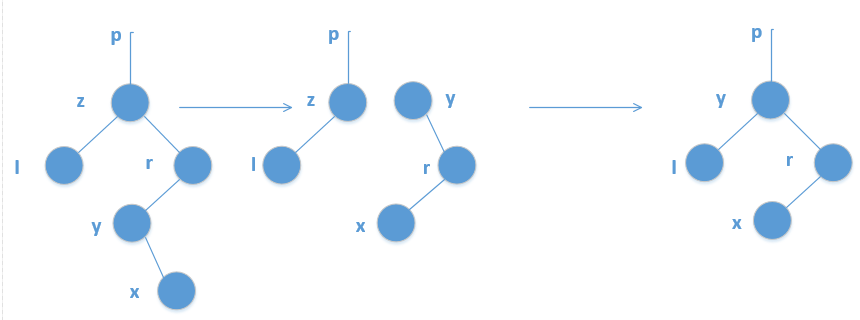
- 删除节点:无论是大根堆还是小根堆,删除的节点都是当前完全二叉树的堆顶元素,接着再将当前完全二叉树的最后一个节点补到原本堆顶的位置,然后再进行自上向下的调整,这一过程被称为“下沉”。
- 构建二叉堆:构建二叉堆,也就是把一个无序的完全二叉树调整为二叉堆,本质上就是让所有非叶子节点依次下沉。
这几种操作都是基于堆的自我调整。
最大堆
所谓的最大堆是指任何一个父节点的值,都大于等于它左右孩子节点的值。例如下图所表示的完全二叉树就是一个最大堆。
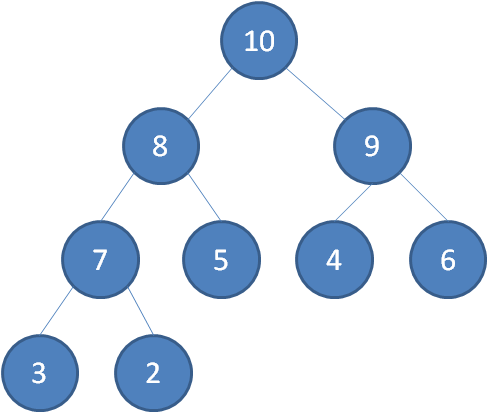
二叉堆的根节点叫做堆顶。最大堆的堆顶是整个堆中的最大元素。
最大堆的插入操作
现在有如下一个大根堆
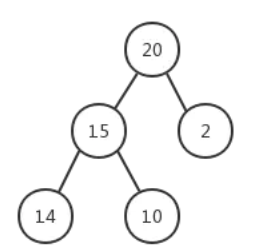
现在我们进行插入操作,插入节点21,即先将它插入到完全二叉树的最后一个位置。

接着进行“上浮”调整


最大堆的删除操作
现在有如下一个大根堆

删除节点20

再将当前完全二叉树的最后一个节点补到原本堆顶的位置

进行“下沉”调整



最大堆的构建
所谓最大堆的构建是指,将n个元素先顺序放入一个二叉树中形成一个完全二叉树,然后来调整各个结点的位置来满足最大堆的特性。
现有如下一个无序完全二叉树

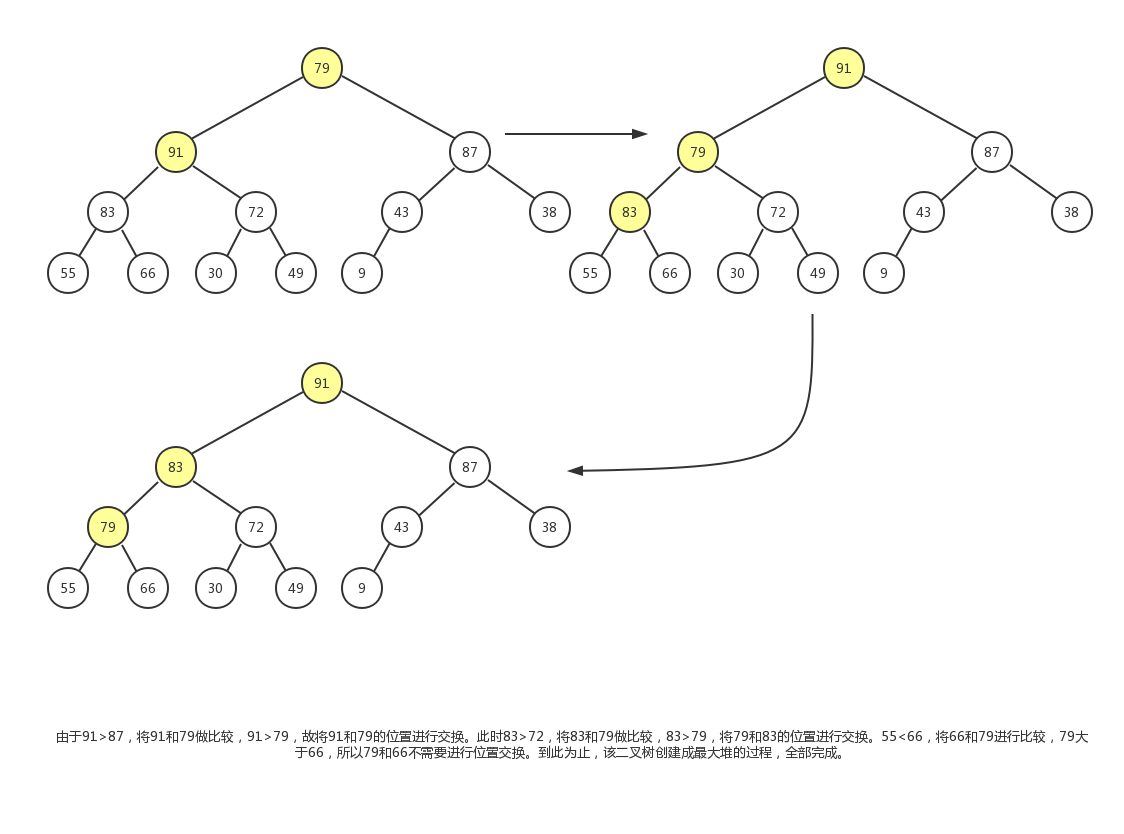
现在要将它变为一个最大堆,首先我们从该完全二叉树中的最后一个非叶子节点为根节点的子树进行调整,然后依次去找倒数第二个倒数第三个非叶子节点...
该完全二叉树的第一个非叶子结点为87
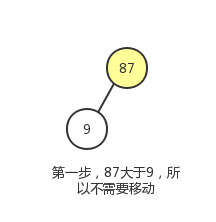
该完全二叉树的第二个非叶子结点为30
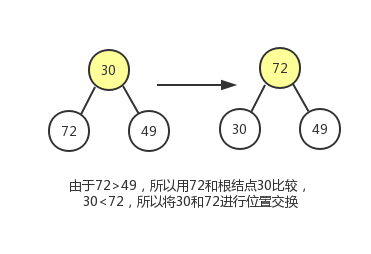
该完全二叉树的第三个非叶子结点为83
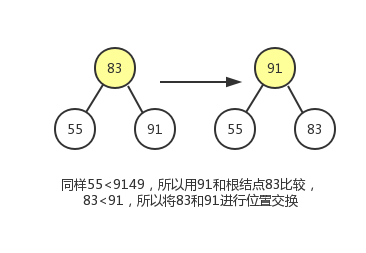
该完全二叉树的第四个非叶子结点为43
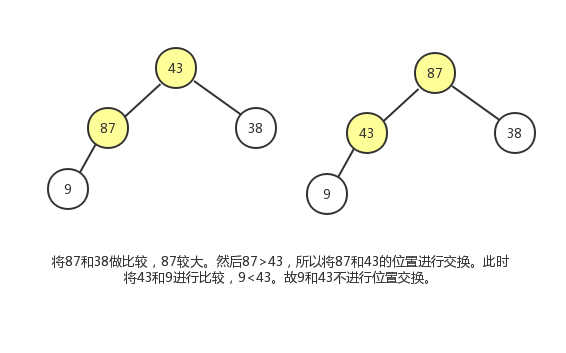
该完全二叉树的第五个非叶子结点为66
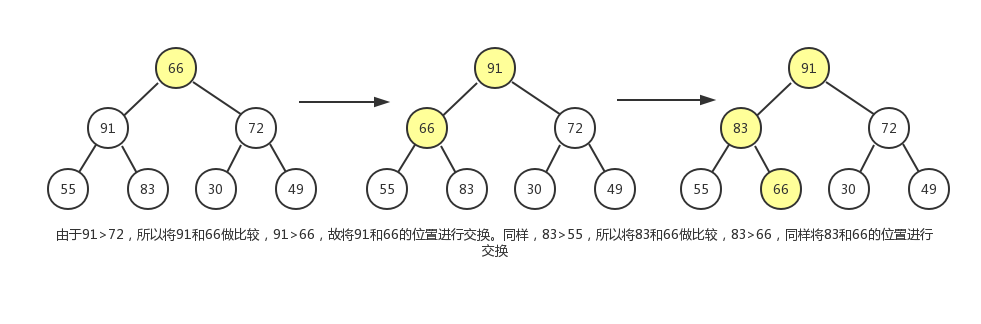
最后到根结点79
最大堆code
void FilterUp(int begin)//上浮操作 插入 大根堆{int j = begin, i = (j - 1) / 2;Type tmp = data[j];while (j > 0){if (data[i] >= tmp) break;data[j] = data[i];j = i;i = (j - 1) / 2;}data[j] = tmp;}void FilterDown(int begin, int end)//下沉操作 删除 大根堆{ int i = begin, j = i * 2 + 1;//j是左孩子Type tmp = data[i];while (j <= end){if (j < end && data[j] < data[j + 1]) ++j;if (tmp >= data[j]) break;data[i] = data[j];i = j;j = i * 2 + 1;}data[i] = tmp;}最小堆
所谓的最小堆是指任何一个父节点的值,都小于等于它左右孩子节点的值。例如下图所表示的完全二叉树就是一个最小堆。
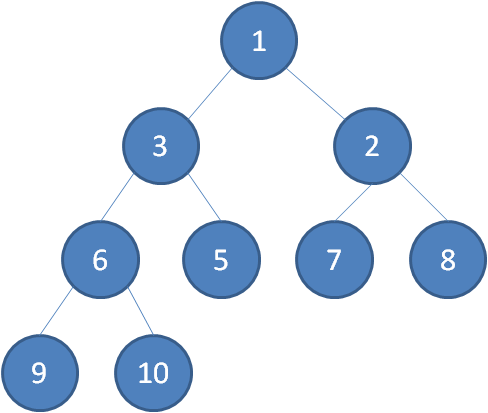
最小堆的堆顶是整个堆中的最小元素。
小根堆的插入操作
二叉堆的节点插入,插入位置是完全二叉树的最后一个位置。比如我们插入一个新节点,值是 0。
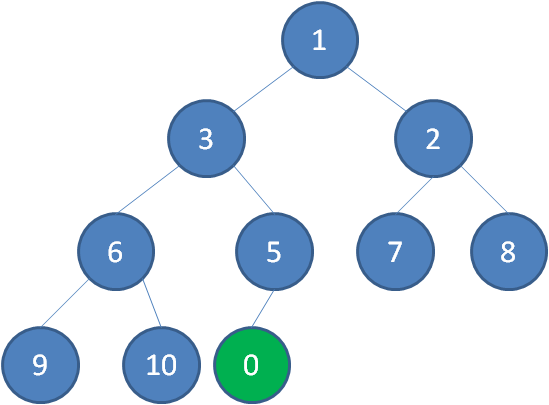
这时候,我们让节点0的它的父节点5做比较,如果0小于5,则让新节点“上浮”,和父节点交换位置。
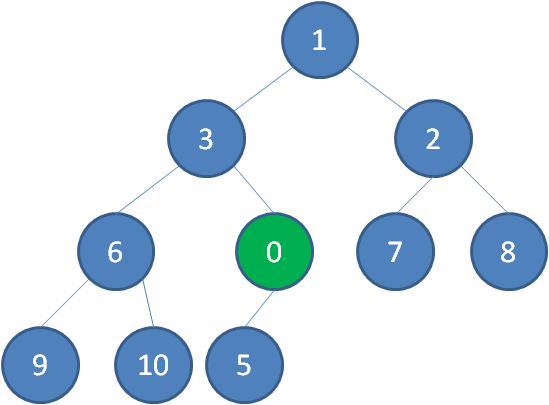
继续用节点0和父节点3做比较,如果0小于3,则让新节点继续“上浮”。
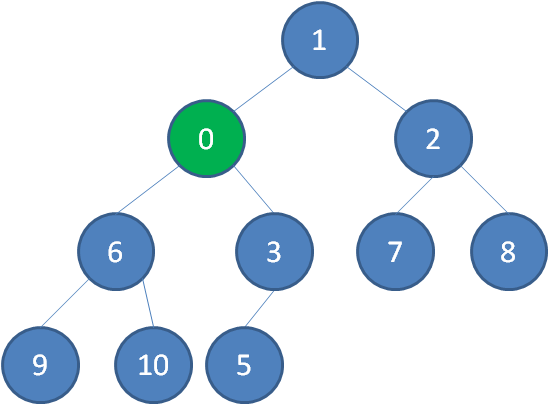
继续比较,最终让新节点0上浮到了堆顶位置。
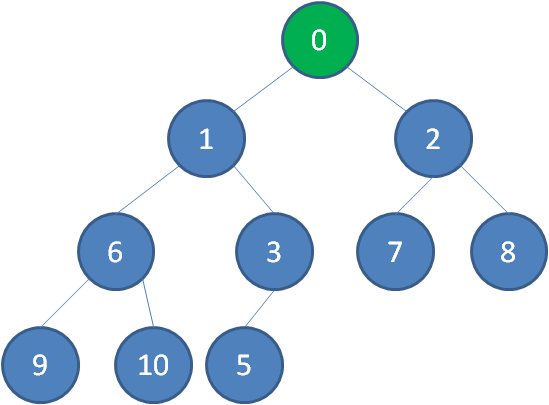
最小堆的删除操作
我们删除最小堆的堆顶节点1。
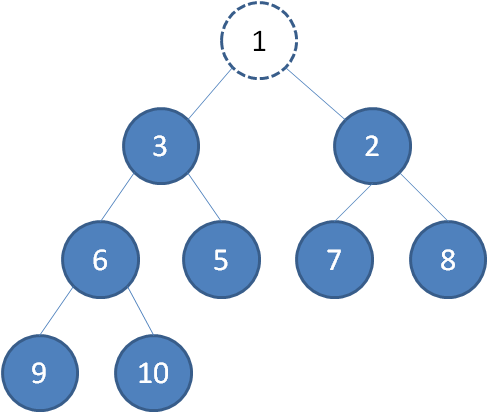
这时候,为了维持完全二叉树的结构,我们把堆的最后一个节点10补到原本堆顶的位置。
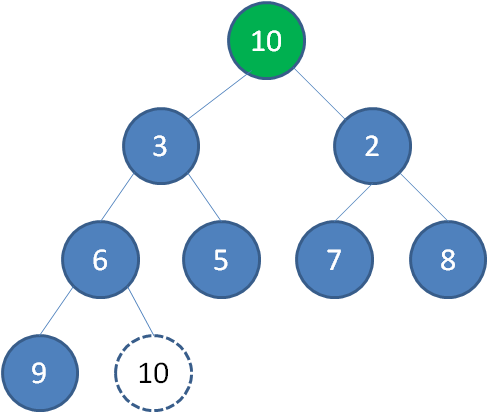
接下来我们让移动到堆顶的节点10和它的左右孩子进行比较,如果左右孩子中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”。
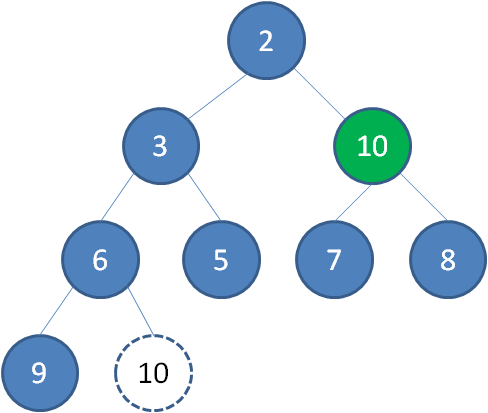
继续让节点10和它的左右孩子做比较,左右孩子中最小的是节点7,由于10大于7,让节点10继续“下沉”。
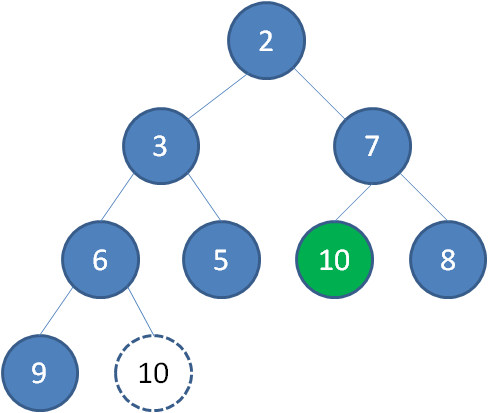
这样一来,二叉堆重新得到了调整。
最小堆的构建
构建二叉堆,就是把一个无序的完全二叉树调整为二叉堆,本质上就是让所有非叶子节点依次下沉。
我们举一个无序完全二叉树的例子:
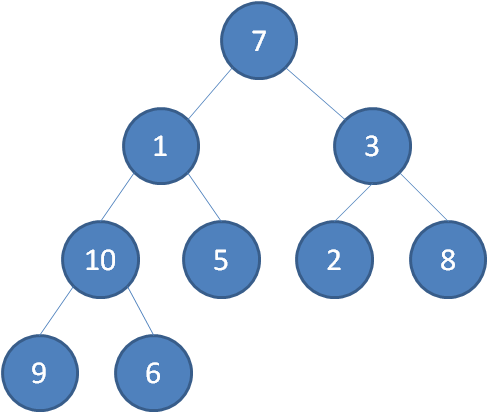
首先,我们从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左右孩子中最小的一个,则节点10下沉。
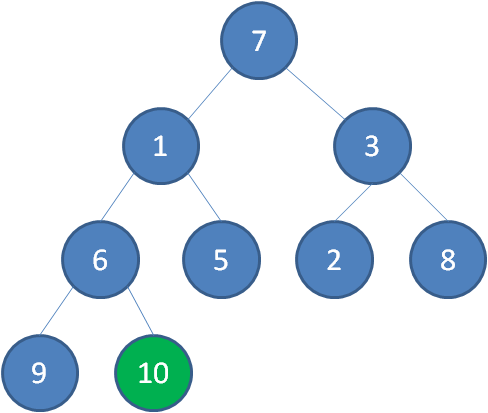
接下来轮到节点3,如果节点3大于它左右孩子中最小的一个,则节点3下沉。
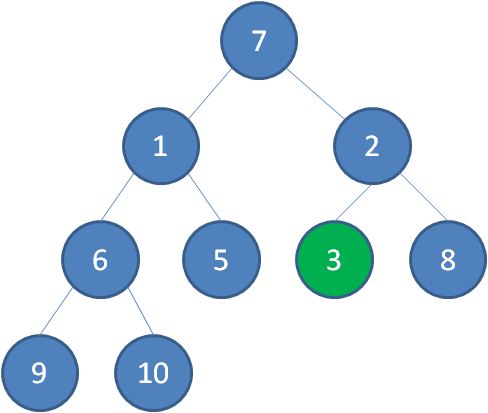
接下来轮到节点1,节点1小于它的左右孩子,所以不用改变。
接下来轮到节点7,如果节点7大于它左右孩子中最小的一个,则节点7下沉。

节点7继续比较,继续下沉。
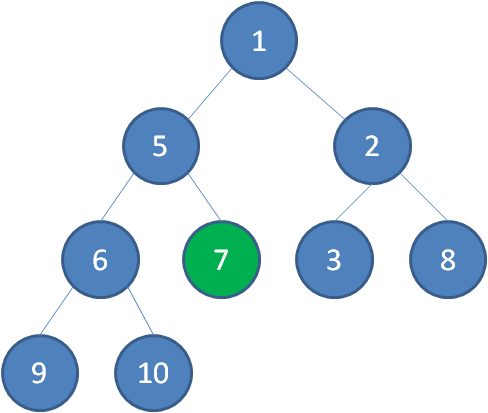
最小堆code
void FilterDown(int begin, int end)//下沉操作 删除 小根堆{int i = begin, j = i * 2 + 1;//i指向根结点Type tmp = data[i];//用来保存当前根结点的值while (j <= end){if (j < end && data[j] > data[j + 1]) ++j;//j指向左右孩子中值较小的那个节点if (tmp <= data[j]) break;//如果当前根结点的值小于它两个孩子,则不需要调整data[i] = data[j];//否则替换根结点和比他小的孩子结点的值i = j;//i指向替换后的根节点的位置j = i * 2 + 1;}data[i] = tmp;}void FilterUp(int begin)//上浮操作 插入 小根堆{int j = begin, i = (j - 1) / 2;Type tmp = data[j];while (j > 0){if (data[i] <= tmp) break;data[j] = data[i];j = i;i = (j - 1) / 2;}data[j] = tmp;}二叉堆的存储方式
二叉堆虽然是一颗完全二叉树,但它的存储方式并不是链式存储,而是顺序存储。也就是说,二叉堆的所有节点都存储在数组当中。
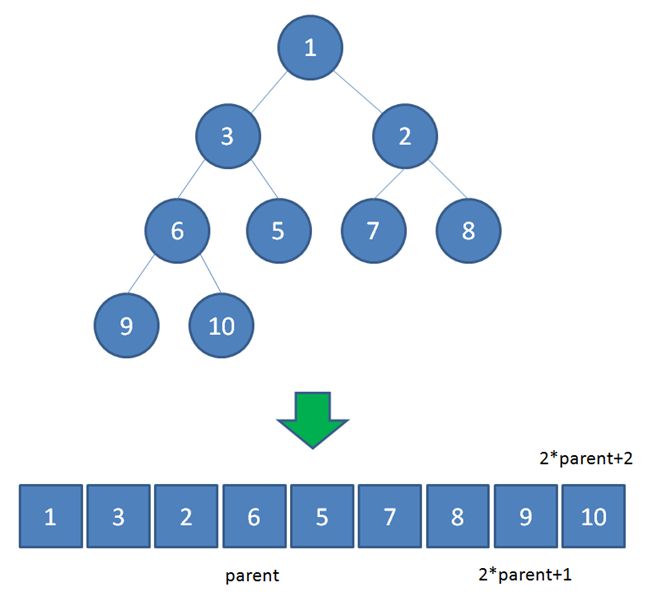
数组中,在没有左右指针的情况下,可以像图中那样,依靠数组下标来计算。
假设父节点的下标是parent,那么它的左孩子下标就是 2*parent+1;它的右孩子下标就是 2*parent+2 。
比如上面例子中,节点6包含9和10两个孩子,节点6在数组中的下标是3,节点9在数组中的下标是7,节点10在数组中的下标是8。
7 = 3*2+1
8 = 3*2+2
原文参考连接:
最大堆(创建、删除、插入和堆排序) - 简书 (jianshu.com)
https://mp.weixin.qq.com/s/cq2EhVtOTzTVpNpLDXfeJg
这篇关于二叉堆 | 大根堆 小根堆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!