Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning

本文主要是介绍Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

这是一篇郑宇团队2019年发表在 **IEEE Transactions on Knowledge and Data Engineering** 杂志上的一篇论文。 从题目来看文章提出的模型是一个多任务模型，在阅读文论之后发现是为了解决两个问题： ①流量预测；（同论文 [上一篇博文介绍的论文一样](https://blog.csdn.net/The_lastest/article/details/85001601)） ②流向预测；（从区域A到区域B的流量预测） 下面就从论文的目的、模型结构和损失函数三个方面来说一下自己的理解。

1. 论文目的

尽管上面已经总结了论文所要解决的主要问题，但笔者认为还是有必要详细介绍一下问题的背景（特别是第二个问题）以便于后面对网络模型的理解。首先，作者在介绍部分提出了从结点和边两个角度(Node-level)来分别解决这两个问题，那么这是怎么定义的呢？

1.1 Node-level

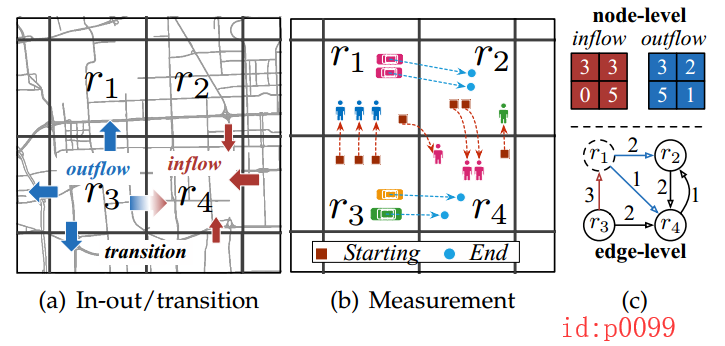
从图p0099所示为将一个大的区域划分成的若干小区域，以$r_1,r_2,r_3,r_4$分别表示4个小的区域。从(b)图中可以看出，流入到4个区域的流量分别为3,3,0,5；从4个区域流出的流量分别为3,2,5,1；此时，就得到了图©中的上面部分，若以时间为坐标轴，我们就能够得到如p0067所示的数据帧。接着，通过对历史数据的学习来预测下一时刻的数据帧。 这就是论文需要解决的第一个流量预测问题。

1.2 Edge-level

所谓从边的角度，就是从原始轨迹数据中，将每个区域之间的人口流向及流量通过一个带权有向图来表示。如图p0099中(a)所示，蓝色和红色箭头分别表示流出和流进的方向。根据(b)中的具体情况，我们就能得到一个带权有向图（©下面部分），其中箭头表示方向，权值表示流量。同时，可以看出，若有N个区域，则对应有向图就有N个顶点，以及理论上有N平方种转移的可能性（只是有很多权值为0的边，而这也导致的数据的稀疏性）。同样，若以时间为坐标轴，我们也能得到一系列这样的有向图；接着通过对历史数据的学习来预测下一时刻的有向图，这样就得到了实体的迁移方向和数量。这就是论文需要解决的第二个问题。

但这样的带权有向图如何喂给一个网络呢？论文作者给出的方案就是将其用向量来表示，如下图所示：

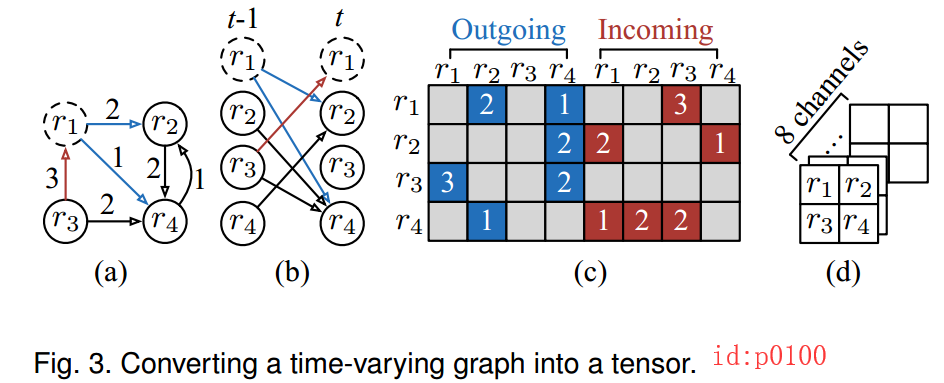
在图p0100中，有向图(a)经过展开后变成了©中所示的两个矩阵。其中左边表示出，右边表示进。例如第一行的2,1,3 分别表示从$r1$到$r2$的流量为2，$r1$到$r4$的流量为1，$r3$到$r1$的流量为3。最后，再将数据组织成(d)中的形式喂给网络进行卷积操作。值得注的是：图©中所有空白的地方都是0，这将导致(d)中每个channel的数据异常稀疏，所以作者提出先对©中的每个行向量进行Embedding操作，然后再构造成(d)的样式喂给网络。

总结一下就是，论文需要解决的就是流量进出和流量迁移方向两个方面的预测；通过对上述两个问题的解决，不仅能够知道每个区域在接下来一个时刻的具体流量，而且还知道了这些流量是从哪个区域转移过来的。

We here define the goal of our paper. Given the historical flow observations {${\mathcal{X}}_t,{\mathcal{M}}_t|t=t_1,\cdots ,t_T$} and external features ${\mathcal{E}}_T$ , we propose a model to collectively predict ${\mathcal{X}}_{t_{T+1}}$ and ${\mathcal{M}}_{t_{T+1}}$ in the future

2. 模型

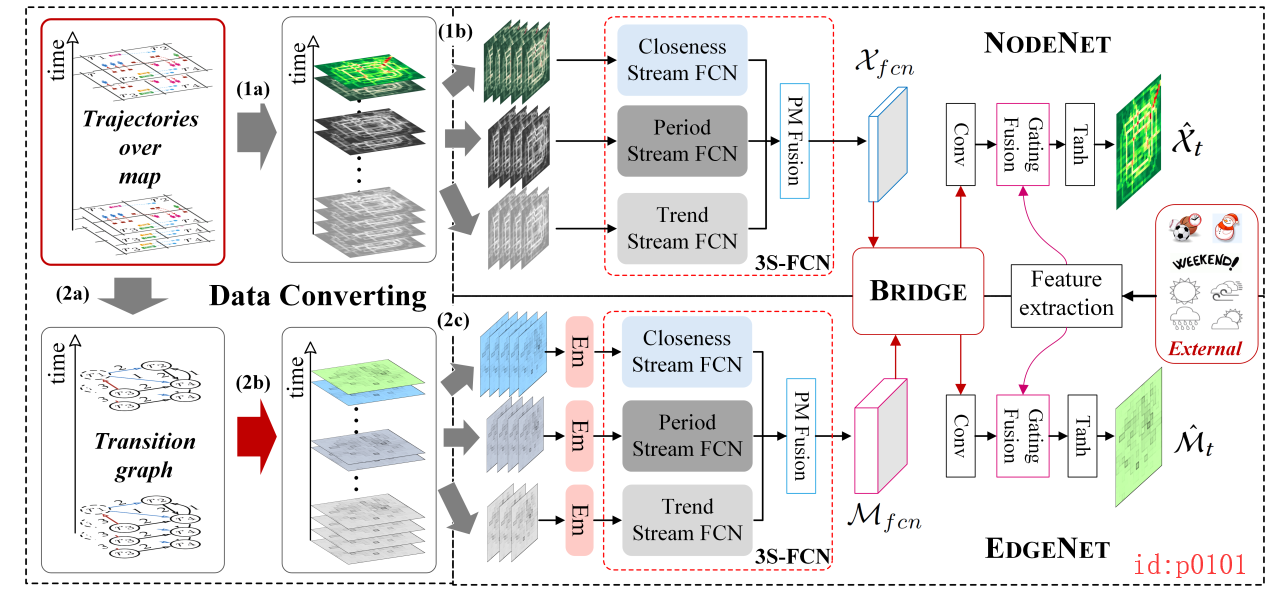
如图p0101所示为整个网络的结构，如果是之前了解过STResNet的话，看到这个结构那就一定不陌生了。从整体上看，整个网络呈对称的结构，上面部分为NodeNet，下面部分为EdegNet。

首先，对于上面的NodeNet来说，原始数据（最左上角）经过(1a)序列化的处理即可喂入到网络中；而对于EdeNet来说，原始数据先要经过(2a)转换为有向图，然后经过(2b)转换成矩阵表示形式再喂给网络（进入网络后首先是Em操作）。

接着，对于上下两个部分的数据来说都将流入到一个名为3S-FCN的模块中（也就是3个FCN），并且上下这两个3S-FCN模块的网络结构都相同，如下图所示。

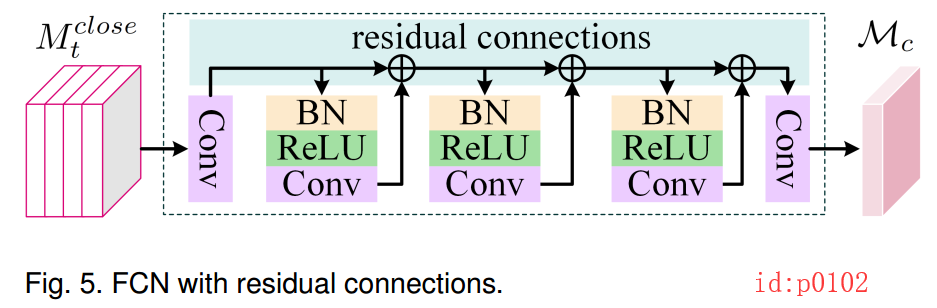
从图p0102可知，这个FCN结构是有一系列的卷积和残差连接构成的，且一目了然就不多说。另外，虽然FCN指的是全连接卷积网络，但在论文中的提现仅仅在于上下两个网络的输入输出大小一致，在这点上和全卷积网络相同，所有作者起了’FCN’这个名字。而其它地方并没有提现出全卷积网络中的“反卷积”操作。 下一步就是对这三个部分的一个融合（作者称为PM融合），以EdegNet为例，其融合方式为：

$${\mathcal{M}}_{fcn}=W_c\odot {\mathcal{M}}_c+W_p\odot {\mathcal{M}}_p+W_q\odot {\mathcal{M}}_q$$

在经过如上步骤之后，NodeNet部分的输出为${\mathcal{X}}_{fcn}$，EdgeNet部分的输出为${\mathcal{M}}_{fcn}$。从网络结构图可以看出，${\mathcal{X}}_{fcn},\mathcal{M}$

这篇关于Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---