线性代数-二次型及其正定性

本文主要是介绍线性代数-二次型及其正定性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

二次型及其矩阵表示形式

二次型:含有n个变量的二次齐次多项式
二次型矩阵:x^TAx,其中A为实对称矩阵
任给一个实二次型,就唯一确定一个实对称矩阵;反之,任给一个实对称矩阵,也可以唯一确认一个实二次型,因此,实二次型与实对称矩阵之间存在一一对应关系,称实对称矩阵A为二次型f的矩阵,二次型f称为实对称矩阵A的二次型,实对称阵的秩也称为二次型f的秩

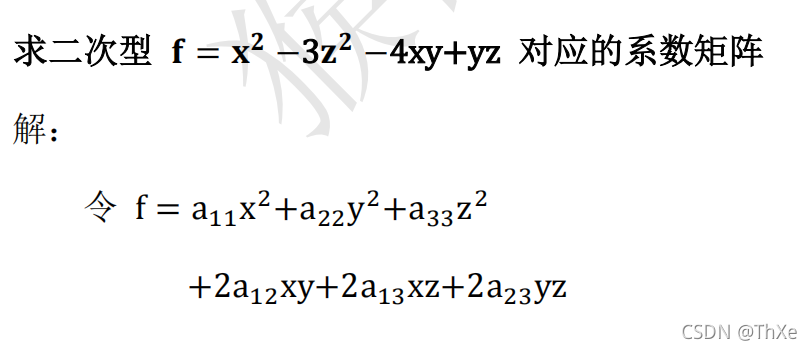
二次型的标准型

只含平方项的二次型称为二次型的标准型
其矩阵形式为y^TAy
其中A=$\left(\begin{array}{ccc}\lambda 1& & \\ & \lambda 2& \\ & & \lambda 3\end{array}\right)$y=$\left(\begin{array}{c}y1\\ y2\\ y3\end{array}\right)$

化二次型为标准型的方法

如果变换矩阵C是可逆矩阵,则称线性变换x=Cy是可逆线性变换.
对于一个二次型我们研究的主要问题是:寻求可逆线性变换x=Cy,化二次型为标准型即求 x=Cy使得
$y=x^{T}Ax=(Cy{)}^{T}A(Cy)=y^T(C^{T}AC)y=y^{T}Ay$
也就是寻求一个可逆矩阵C使得C^TAC=A,其中A为对角矩阵

正交变换法化二次型为标准型

(1)将二次型表示为矩阵形式f=x^TAx(A为实对称矩阵)
(2)求出A的特征值$\lambda 1.....\lambda n$
(3)求出A的特征向量
(4)将特征向量正交化并单位化
(5)标准型:$f=\lambda 1y_1^2.....+\lambda n{y}_n^2$
(6)交换矩阵P为A的可逆变化矩阵

配方法把二次型化成标准型

把标准矩阵化为规范型

矩阵正定性

这篇关于线性代数-二次型及其正定性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---