本文主要是介绍【文献分享】freud 程序: 用于原子模拟数据的高通量分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
![]()
================================
分享一篇用于原子模拟数据高通量分析的程序:freud 。
感谢论文的原作者!
================================
主要内容
“ freud 程序是一个用于分析仿真数据的库。考虑到现代模拟和数据分析工作流程,freud 提供了一个 Python 接口,用于在笔记本电脑、工作站和超级计算集群上高效运行的快速并行 C++ 例程。该软件包提供了在周期系统中寻找粒子邻居的核心工具,并为使用这些工具实现的各种方法提供了统一的 API。因此,freud 用户可以同样轻松地访问标准方法,例如径向分布函数以及更新、更专业的方法,例如平均力和扭矩的潜力以及局部晶体环境分析。而不是提供自己的轨迹数据结构,freud 直接在 NumPy 数组或其他 Python 包提供的轨迹数据结构上运行。这种设计允许freud 通过利用其他轨迹管理工具的文件解析能力与许多轨迹文件格式透明地交互。通过对其数据源保持不可知,freud 适用于分析任何粒子模拟,无论原始数据表示或模拟方法如何。当与 HOOMD-blue 等可编写脚本的模拟软件结合用于实时分析时,freud 可以实现适应系统当前状态的智能模拟,从而允许用户研究成核和生长等现象。”——取自文章摘要。
================================
Additional comments including restrictions and unusual features:
1. freud provides very fast parallel implementations of standard analysis methods like RDFs and correlation functions.
2. freud includes the reference implementation for the potential of mean force and torque (PMFT).
3. freud provides various novel methods for characterizing particle environments, including the calculation of descriptors useful for machine learning.
================================
Figure 1
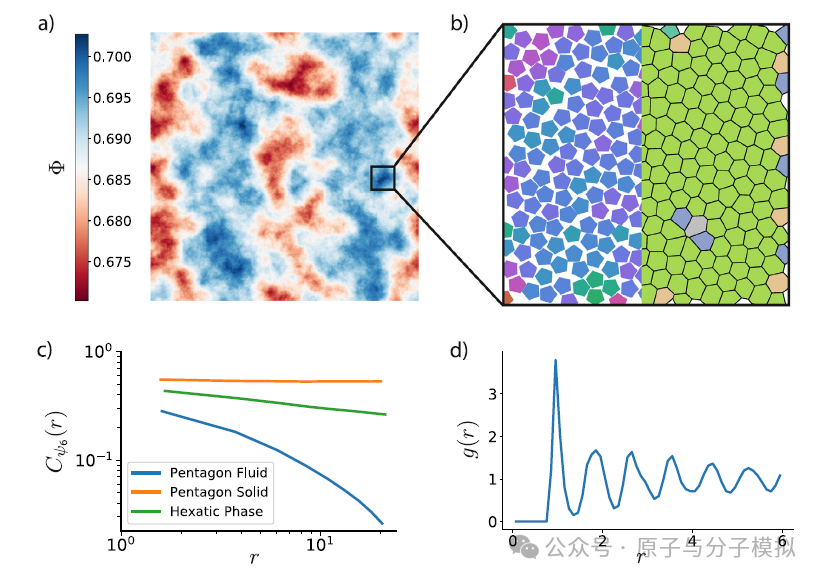
Figure 2
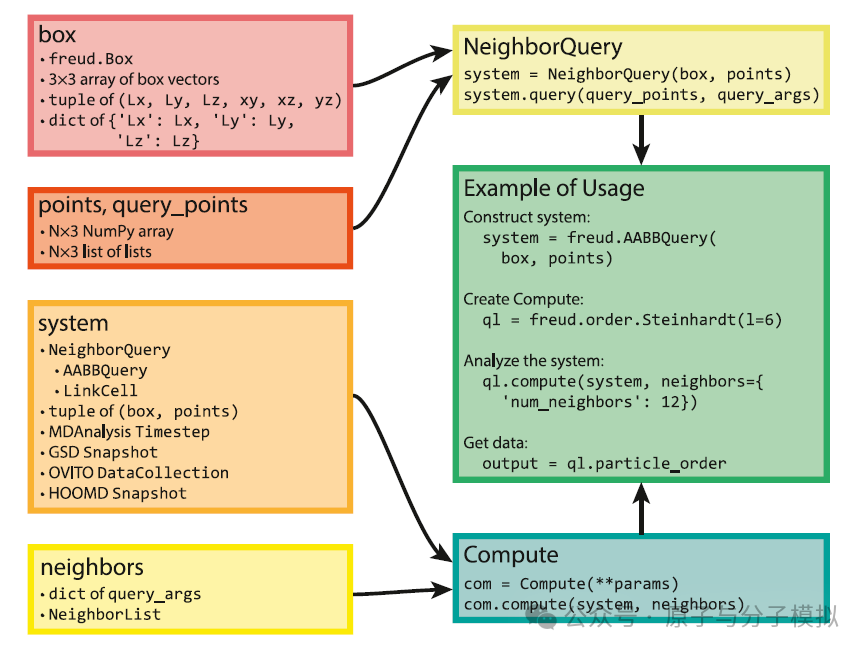
Figure 3
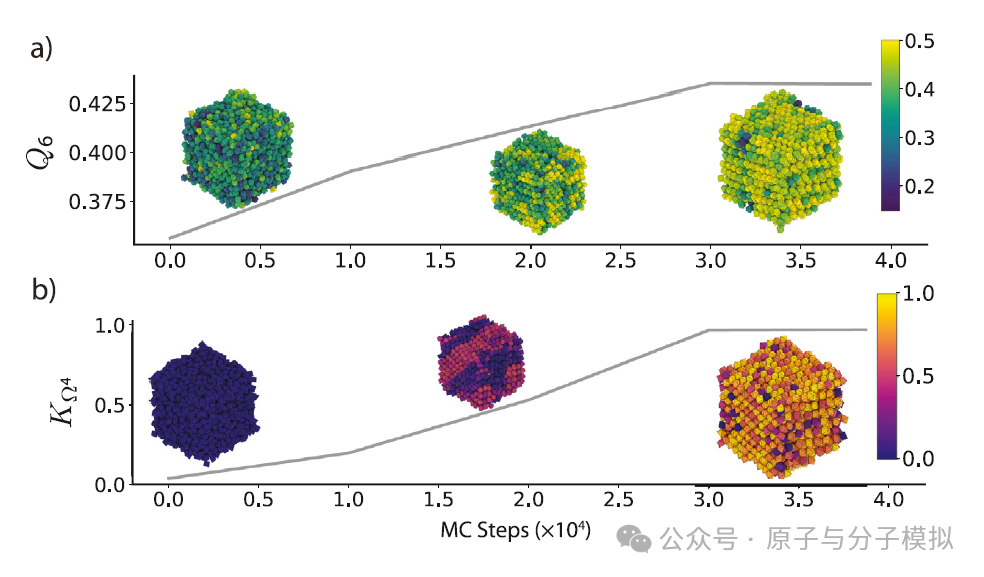
Figure 4
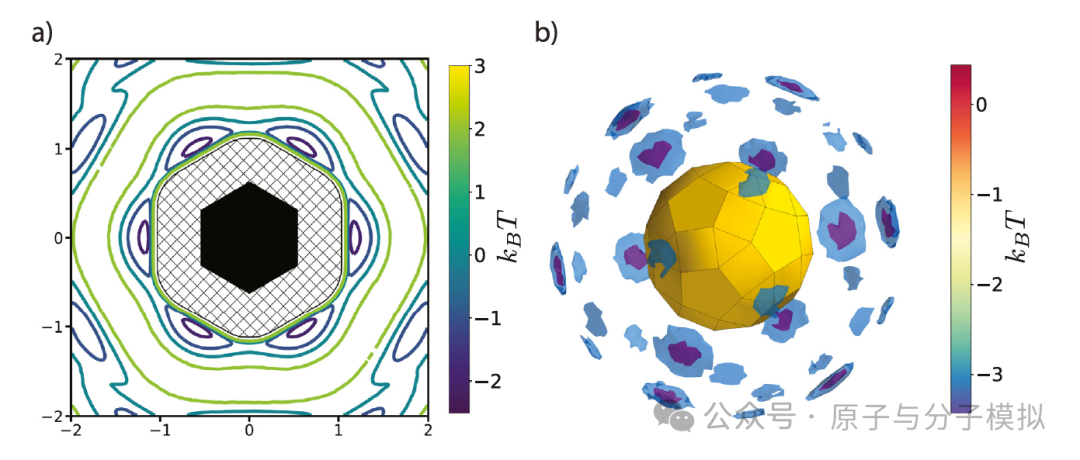
Figure 5
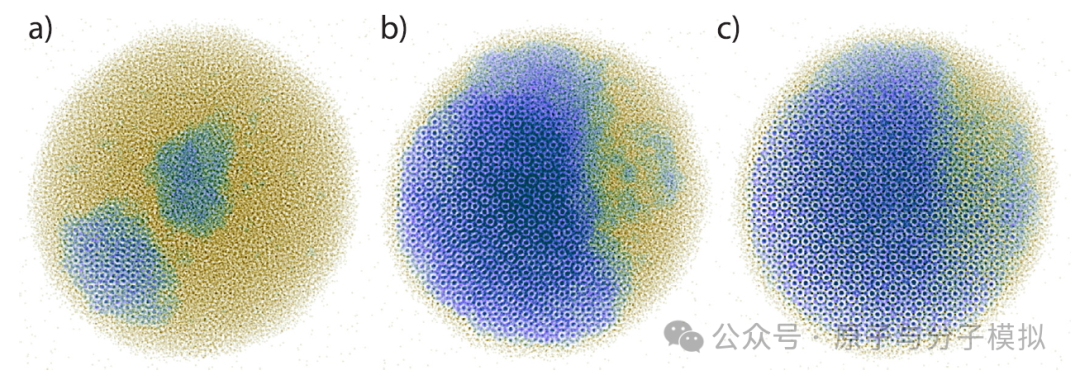
Figure 6
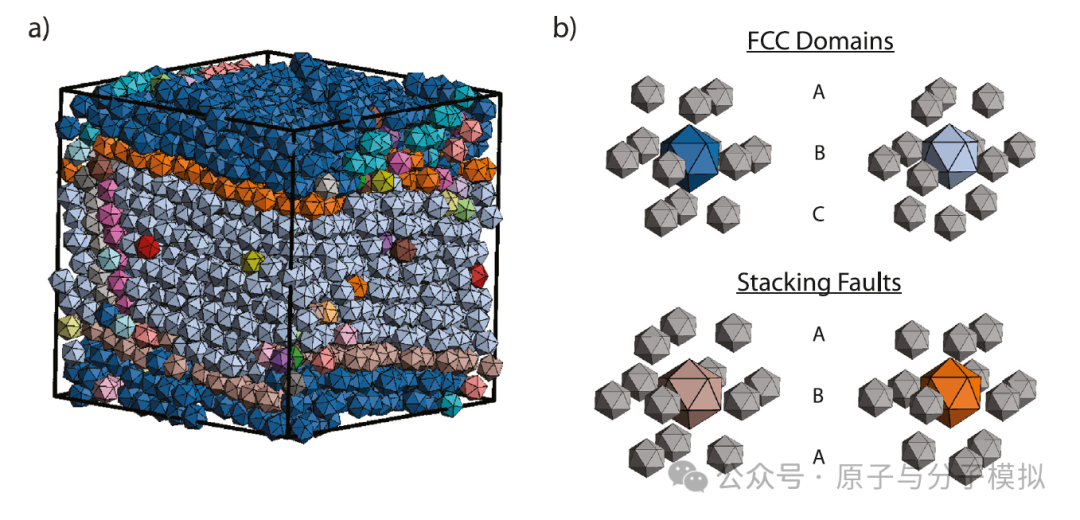
Figure 7

================================
Analysis Modules
These introductory examples showcase the functionality of specific modules in freud, showing how they can be used to perform specific types of analyses of simulations.
-
freud.cluster.Cluster and freud.cluster.ClusterProperties
-
freud.density.CorrelationFunction
-
freud.density.GaussianDensity
-
freud.density.LocalDensity
-
freud.density.RDF: Accumulating g(r) for a Fluid
-
freud.density.RDF: Choosing Bin Widths
-
freud.diffraction.DiffractionPattern
-
freud.diffraction.Static Structure Factor Direct and freud. diffraction. Static Structure FactorDebye
-
freud.environment.AngularSeparation
-
freud.environment.BondOrder
-
freud.environment.EnvironmentCluster
-
freud.environment.LocalDescriptors: Steinhardt Order Parameters from Scratch
-
freud.interface.Interface
-
freud.order.Hexatic: Hard Hexagons
-
freud.order.Hexatic: 2D Minkowski Structure Metrics
-
freud.order.Nematic: Nematic Order Parameter and the Nematic Tensor
-
The Nematic Order Parameter
-
Calculating the Nematic Order Parameter
-
Example 1: A Disordered System
-
Example 3: Different Degrees of Orientational Order
-
freud.order.Steinhardt
-
freud.pmft.PMFTXY
-
freud.pmft.PMFTXYZ: Shifting Example
================================
Example Analyses
The examples below go into greater detail about specific applications of freud and use cases that its analysis methods enable, such as user-defined analyses, machine learning, and data visualization.
-
Implementing Common Neighbor Analysis as a custom method
-
Analyzing simulation data from HOOMD-blue at runtime
-
Analyzing GROMACS data with freud and MDTraj: Computing an RDF for Water
-
Analyzing data from LAMMPS
-
Using Machine Learning for Structural Identification
-
Handling Multiple Particle Types (A-B Bonds)
-
Calculating the Radial Distribution Function (RDF) from Simulation Data
-
Calculating Strain via Voxelization
-
Visualizing analyses with fresnel
-
Visualization with plato
-
Visualizing 3D Voronoi and Voxelization
================================
部分例子
Figure 8 radial distribution function (RDF)
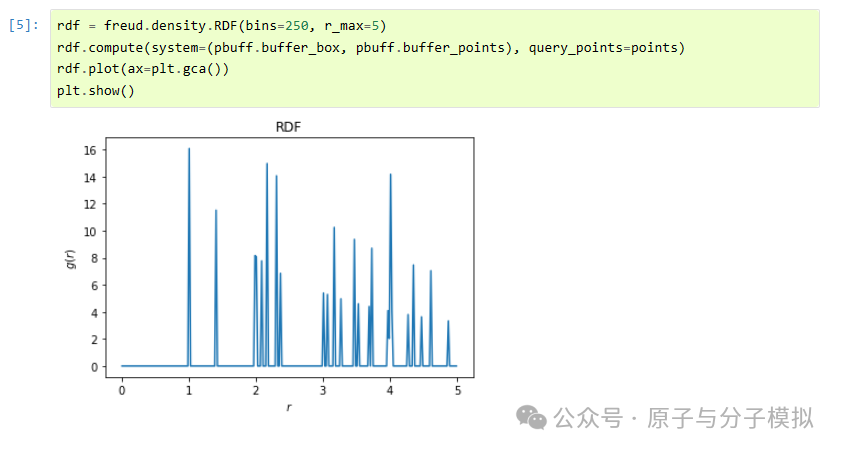
Figure 9 Voronoi diagram
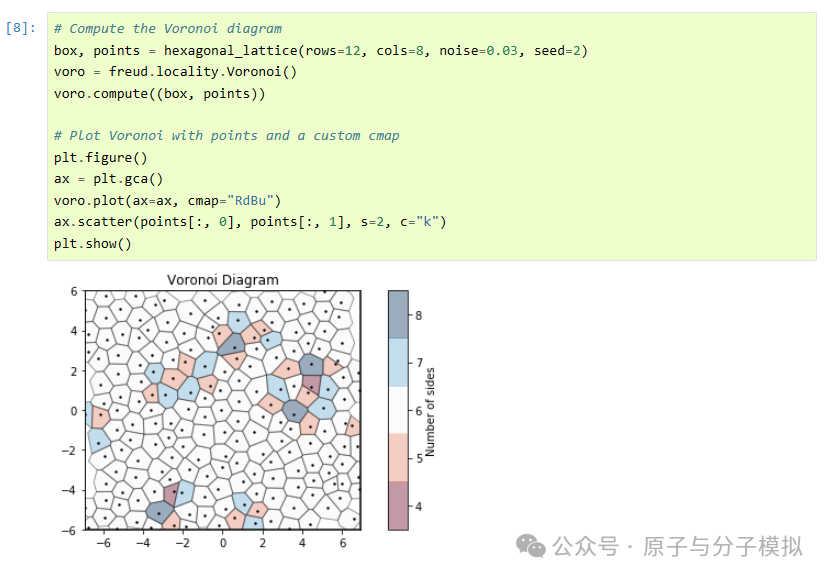
Figure 10 Cluster identified
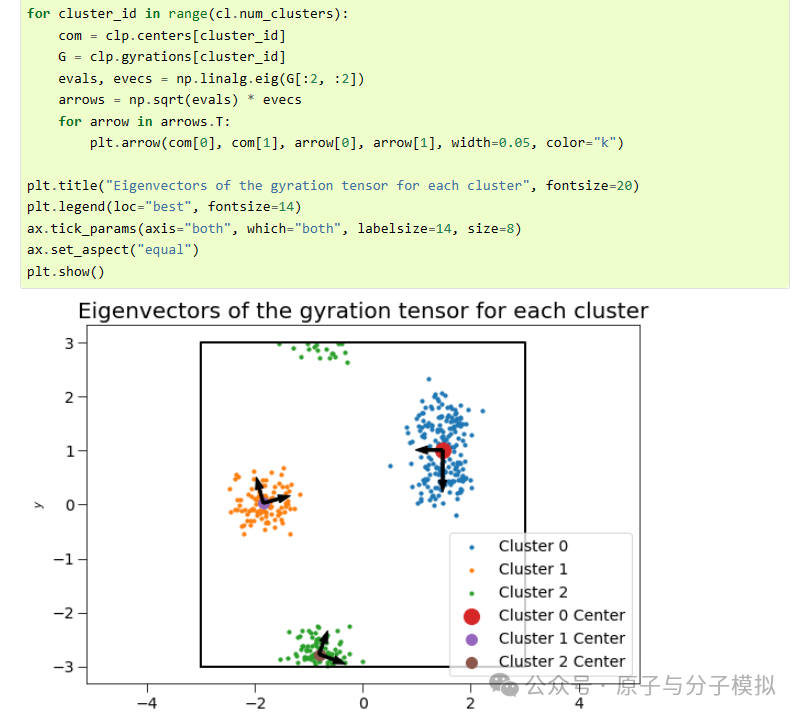
Figure 11 Compute the correlation functions
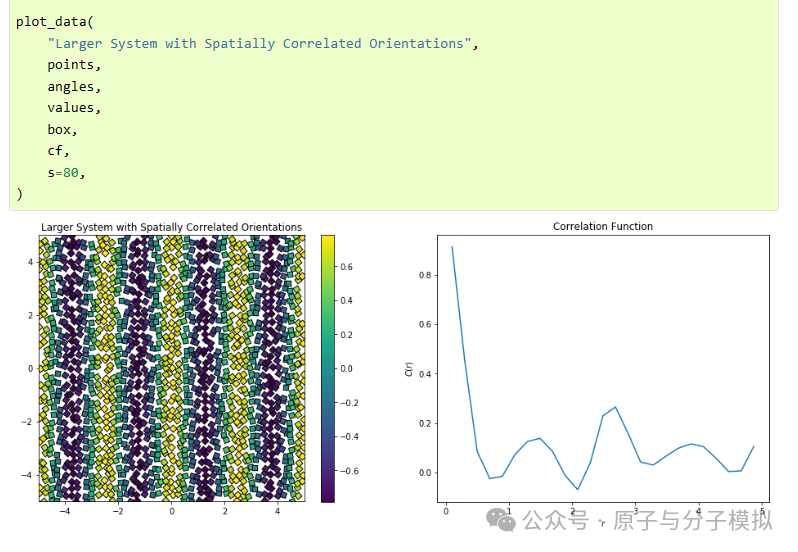
Figure 12 Gaussian density calculation

Figure 13 local density calculation
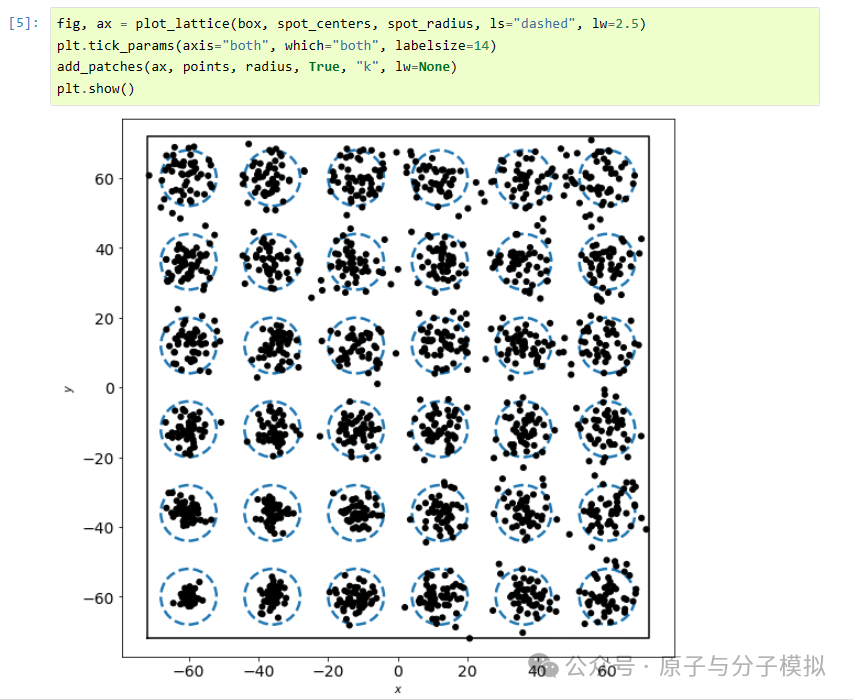
Figure 14 calculation of the radial distribution function
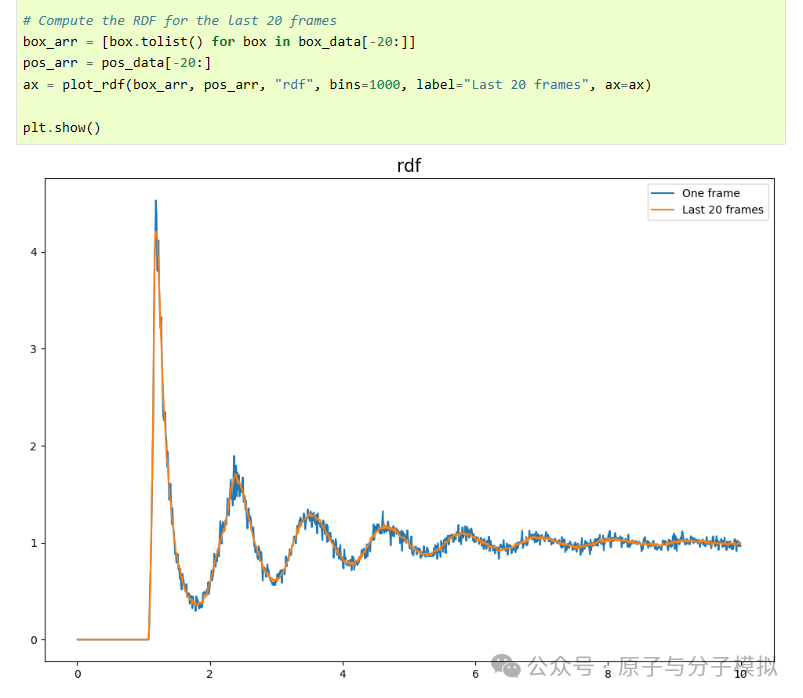
Figure 15 DiffractionPattern
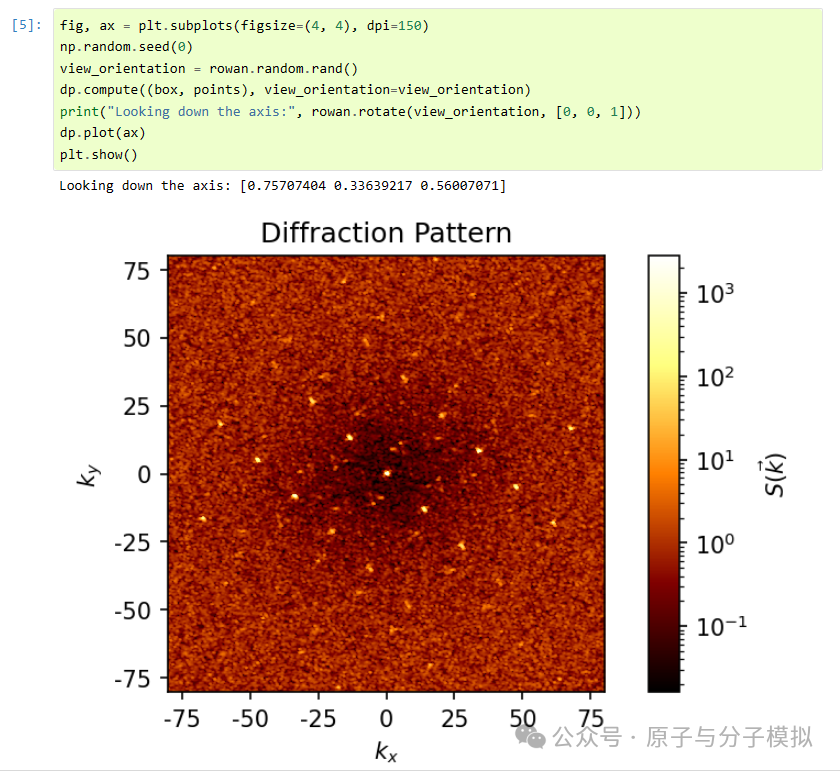
Figure 16 Static Structure Factor
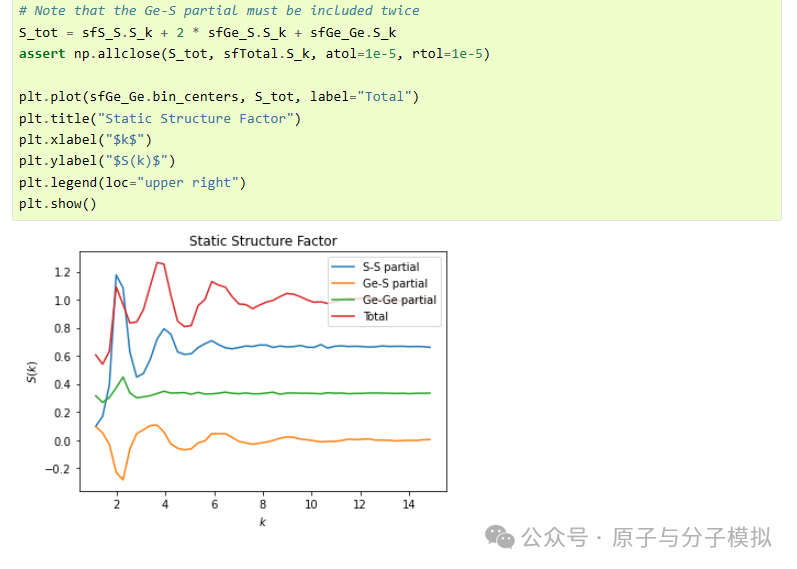
Figure 17 Angular Separation class
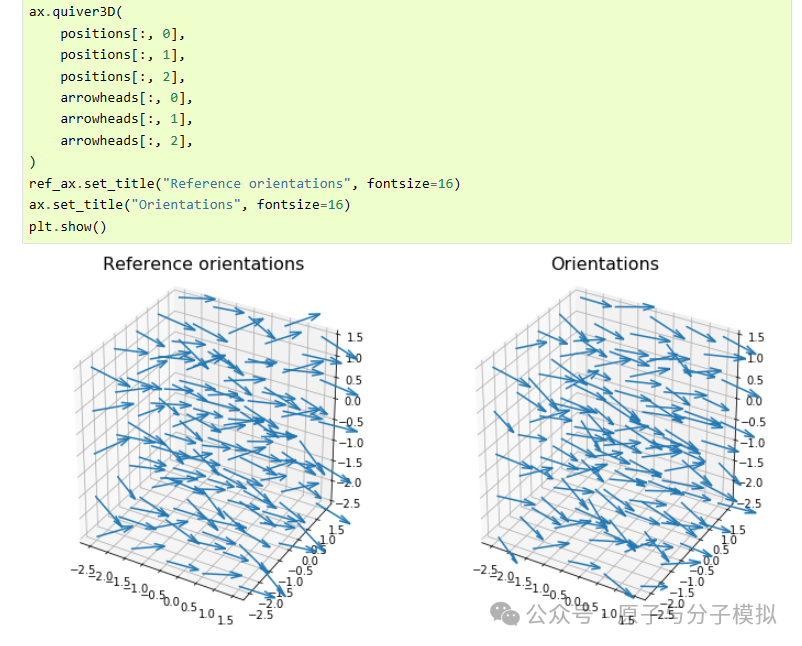
Figure 18 Computing the Bond Order Diagram

Figure 19 Particle Local Environment
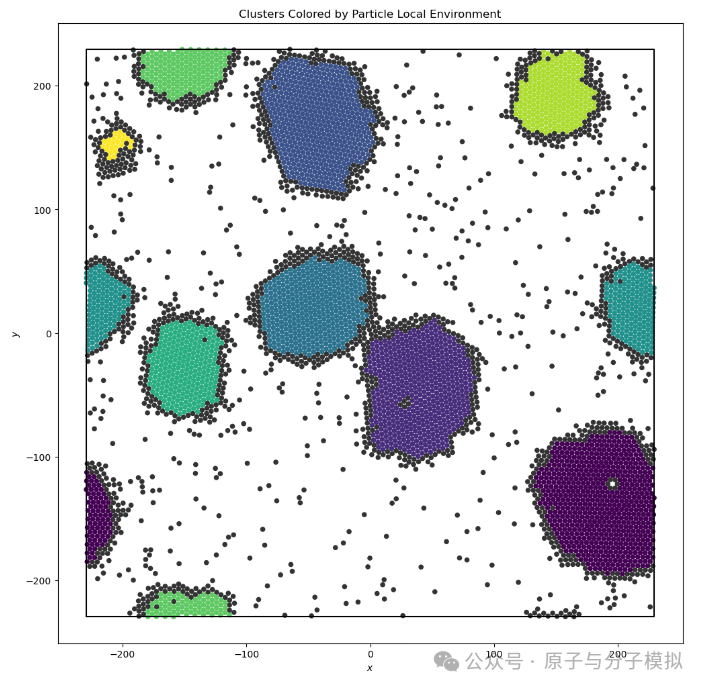
Figure 20 Locating Particles on Interfacial Boundaries
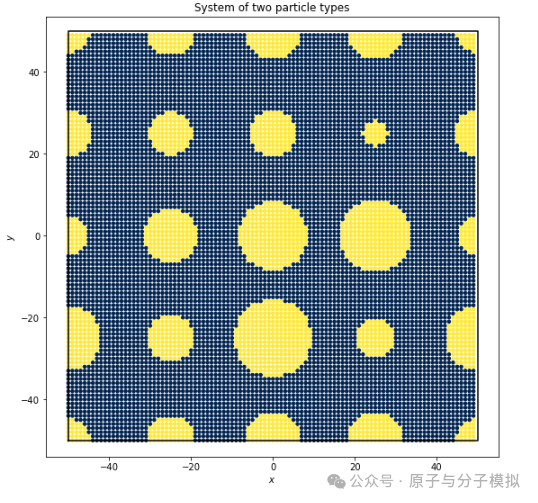
Figure 21 Hexatic Order Parameter
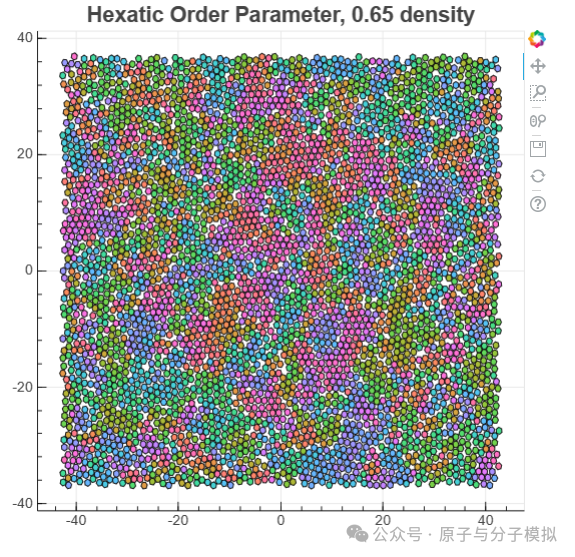
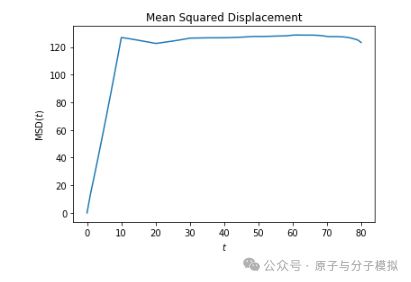
Figure 22 Mean Squared Displacement
================================
![]()
以上是我们分享的一些经验或者文章的搬运,或有不足,欢迎大家指出!
如有侵权,请联系我立马删除!
详细内容(文章题目、文章链接、附件下载)可在微 信 公 众 号:原子与分子模拟获取,欢迎大家关注。

这篇关于【文献分享】freud 程序: 用于原子模拟数据的高通量分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





