雷达系列论文翻译（九）：3D Scan Registration Using the Normal Distributions Transform

3D Scan Registration Using the Normal Distributions Transform with Ground Segmentation and Point Cloud Clustering

这篇论文是之后的第十篇论文的简述版，两者基本上没有区别，这里提到的贪婪聚类就是下一篇讲到的区域生长聚类方法

摘要

正态分布变换(NDT)扫描配准算法将环境建模为一组高斯分布，并通过将环境离散为体素来生成高斯分布。对于标准方法，NDT算法倾向于即使对于适度的初始变换误差也具有较差的收敛性。本文提出了一种分割贪婪聚类NDT(SGC-NDT)变体，它利用环境中的自然特征为NDT算法生成高斯聚类。通过分割地面和聚类剩余特征，SGC-NDT方法产生了平滑和连续的代价函数，这保证了优化将收敛。实验表明，在城市和森林环境中，与其他最先进的方法相比，SGC-NDT算法的扫描配准精度更高，收敛性能更好。

引言

扫描配准算法在移动机器人地图绘制算法中具有重要作用。许多传感器以点云的形式提供关于环境的信息，例如RGBD摄像机、LIDAR和双目相机。扫描配准算法依靠扫描之间的重叠几何来确定两次扫描之间的相对变换。了解变换参数有助于点云数据的聚合，这是未知环境中自主操作通常需要的。

最常见的扫描配准算法是迭代最近点算法。ICP算法由Besl和McKay[1]、Chen和Medioni[2]以及Zhang[3]独立介绍。ICP算法试图找到变换参数，使得最近邻点之间的欧几里得距离最小化。ICP算法没有考虑点云的表面级别的特征，因为它是在点的级别上运行的。此外，ICP假设两个点云可以完美重叠，然而实际上，由于噪声和传感器的采样特性，情况并非如此。为了解决ICP的不足，Segal等人引入了广义ICP (G-ICP) [4]，该方法使用局部邻域计算每个点的表面法线，并且仅包括两次扫描之间具有相似表面结构的点之间的对应关系。ICP算法的主要瓶颈是识别最近邻的点所需的最近邻搜索算法，它通常是计算昂贵的。

正态分布变换(NDT)是一种替代方法，由Biber和Strasser首次提出用于2D情况下的扫描配准和建图[5]。后来，Magnusson等人[6]将其扩展用于三维点云，Stoyanov等人[7]将其进一步扩展为分布到分布的配准问题。NDT算法的优势在于，它不需要显式计算最近邻对应关系，因为它将扫描表示为一组高斯分布，而不是单个点。NDT算法还将底层扫描表示为一组高斯分布，将表面局部建模为生成的分布。这是一种基于优化的方法，用于确定变换参数，从而最大化从NDT分布中采样到扫描的可能性。

NDT的标准公式导致非线性优化，当从明显偏离真实变换的初始估计开始时，非线性优化容易导致较差的收敛特性。NDT使用基于体素的离散化来产生高斯分布，它不一定精确地模拟环境。该分布仅局部地建模每个栅格单元内的点，并且可能无法捕捉扫描中存在的更广泛的特征。此外，在优化过程中栅格单元边界之间的交叉点导致代价函数是不连续的。在此之前，作者[8]提出了多尺度k-均值NDT(MSKM-NDT)，它利用多尺度上的k-均值聚类，用一种由粗到细的优化方法对2D激光扫描进行分割。虽然MSKM-NDT方法避免了局部极小值，提高了收敛性，并产生了平滑连续的代价函数，但聚类数必须是先验已知的。

Moos-mann等人也在3D中执行了扫描分割，他们使用基于图的方法基于局部凸性标准分割激光扫描[9]。基于图的方法计算表面法线信息，以便对扫描进行分割，然而，对于稀疏的激光扫描，或者当环境由诸如树木、灌木丛和树叶等对象组成时，很难生成高质量的表面法线信息。Douillard等人演示了使用高斯过程和增量采样一致性的扫描分区应用于ICP扫描配准的效果，其中相邻点之间的对应关系被限制为属于相应的分区[10]。

这项工作的贡献是应用分割和聚类算法来提高NDT算法的准确性和收敛性，特别是对于具有稀疏点云的户外开放环境。进行地面分割是为了分离环境中通常与地面分离的自然特征。代表环境的自然特征用于为NDT算法生成高斯聚类，这是可取的，因为与标准NDT算法相比，它允许使用明显更少的分布对环境进行精确建模。地面分割的应用导致环境分解为地面和障碍物分区，这些分区可用于更高级别的任务执行。

为了实现分解，将基于高斯过程回归[11]和增量采样一致性[12]的地面分割算法应用于三维激光扫描。然后提出了一种贪婪聚类算法，将非地面点划分成聚类。假设非地面点被完全和地面点分离开来，贪婪聚类算法生成聚类，该聚类将属于环境中分割后特征的点(例如树、灌木丛等)组合在一起。分割后的特征聚类被用来构建NDT算法的高斯分布。对NDT算法进行了修改，以评估所有生成的聚类的代价函数，这保证了非线性优化被很好地定义，并且所有标准的非线性优化算法将收敛到满足最优性必要条件的解[13]。对NDT算法的点对分布和分布对分布变体进行了评估。使用从福特校园数据集[14]和伍斯特理工学院的一个稀疏森林公园获得的激光数据，对所提出的方法的准确性和收敛性进行了评估。

问题描述

扫描配准算法寻求在两点云扫描、即参考扫描和场景扫描之间找到最佳变换。目标是确定最佳对齐两次扫描的转换参数，使它们尽可能重叠。将参考扫描表示为一组点 Y = { y 1 , . . . , y N y } Y = \{ y_1,...,y_{N_y} \} Y={y1​,...,yNy​​}其中 y i ∈ R 3 , i ∈ { 1 , . . . , N Y } y_i \in \mathbb{R}^3 ,i \in \{1,...,N_Y\} yi​∈R3,i∈{1,...,NY​}以及场景扫描 X = { x 1 , . . . , x N x } X = \{ x_1,...,x_{N_x} \} X={x1​,...,xNx​​}其中 x j ∈ R 3 , j ∈ { 1 , . . . , N X } x_j \in \mathbb{R}^3 , j \in \{1,...,N_X\} xj​∈R3,j∈{1,...,NX​}。一个点$x_j$由三个部分组成， x j = { x j x , x j y , x j z } x_j = \{ x_j^x, x_j^y, x_j^z \} xj​={xjx​,xjy​,xjz​}，分别指该点的$x$，$y$和$z$部分。使用参数估计$p=[t_x，t_y，t_z，\phi ，\theta ，\psi {]}^T\in {\mathbb{R}}^3\times \mathbb{S}\mathbb{O}(3)$将点$x$从场景扫描映射到参考扫描的坐标系的
$$T(p,x)=[R_{\phi }{R}_{\theta }{R}_{\psi }]x+{\left[\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right]}^T$$
其中，$R_{\phi }$是绕$x$轴旋转角度$\phi$的旋转矩阵，$R_{\theta }$是绕$y$轴旋转角度$\theta$的旋转矩阵，$R_{\psi }$是绕$z$轴旋转角度$\psi$的旋转矩阵，以及$[t_x，t_y，t_z]$是两帧之间的平移向量。

本文提出的方法

为了提高NDT算法的准确性和收敛性，提出了分割后贪婪聚类的NDT(SGC-NDT)方法。SGC-NDT方法对地面点进行分割，并对其余点进行聚类。地面点的分割和贪婪聚类算法的应用被应用于点对分布和分布对分布的NDT配准方法。

NDT算法在以下三个方面进行了修改：

1)

使用第四节中描述的地面分割方法去除扫描中的地面点。在大型户外场地等环境中，地面点的收集是多余的，并且不能像其他环境特征(如大树、栅栏等)那样为扫描匹配提供更多信息。扫描点密度也成为一个问题，因为非常靠近激光传感器的地面点比更远的地面点的密度大得多，这对于NDT来说是不可取的，因为车辆附近的高密度点会产生偏向传感器原点的高斯分布。使用基于体素的下采样滤波器可以在一定程度上减轻有偏分布的影响，但是滤波会给扫描配准增加额外的计算，并从整个扫描中移除有用的信息。虽然对扫描进行下采样可以减轻NDT的偏差分布问题，但它不能解决代价函数不连续的问题。

2）

使用第五节中描述的贪婪聚类方法对非地面点进行聚类。通过执行聚类步骤，环境中的自然特征(如树木和灌木丛)被聚类以形成SGC-NDT的高斯分布。相比之下，NDT执行基于体素的离散化，生成截断的高斯分布，不一定能正确建模环境。

3）

为了适应扫描聚类的贪婪聚类方式，NDT代价的计算按照第七节所述进行了修改。NDT评估被转换点所在单元内的高斯分布。SGC-NDT算法评估由被转换点在贪婪聚类方法识别的聚类的高斯分布。类似地，对于分布对分布的NDT匹配方法，场景中的每个高斯分布根据参考扫描的所有高斯分布进行评分。在所有高斯分布上的评估在计算上是可行的，因为在扫描中识别的聚类的数量通常比基于体素的离散化产生的高斯分布的数量小得多。基于扫描中的所有高斯分布计算代价允许最强的贡献来自最可能的聚类，并为优化提供了连续且可微的代价函数。

地面分割

用于这项工作的地面分割算法的基础首先由Douillard等人[12]提出。他们的方法基于稀疏点云的2D高斯过程(GP)模型执行地面分割，该模型使用增量采样一致性(INSAC)方法提供了识别地面点的概率框架。Tongtong等人[15]提出了一种改进的Douillard地面分割算法。为了减少计算量，Tongtong基于径向栅格bin将扫描划分为多个扇区，并将地面分割分别应用于每个扇区。高斯过程回归被表述为基于包含在每个扇区中的点的近似。Tongtong的方法被证明比2D的方法运行得更快，在分割质量上有相当的结果。本文采用了[15]中的1D近似地面分割法，并在本节中作了简要总结。

为了执行径向栅格绑定，激光坐标系中的激光扫描的$xy$平面首先被分割成$N_s$个角扇区，其中第$i$个角扇区被表示为${\zeta }_i$。每个扇区被进一步细分成$N_b$个基于线性范围的bin，它将扇区细分为 ζ i = { ζ i 1 , . . . , ζ i N b } \zeta_i = \{\zeta_i^1, ..., \zeta_i^{N_b} \} ζi​={ζi1​,...,ζiNb​​}。最后，从扫描$Y$得到的位于第$i$个扇区的第$j$个bin内的点被表示为 ( s i j ) Y = { y ∈ Y ： y ∈ ζ i j } , i ∈ { 1 , . . . , N s } , j ∈ { 1 , . . . , N b } (s_i^j)^Y = \{ y \in Y：y \in \zeta_i^j \}, i \in \{1, ..., N_s\}, j \in \{1,...,N_b\} (sij​)Y={y∈Y：y∈ζij​},i∈{1,...,Ns​},j∈{1,...,Nb​}。定义$S_Y$表示所有单独点集$(s_i^j{)}^Y$的集合，以及接受扫描$Y$并返回径向bin栅格集合的函数，$S_Y=\tau (Y)$。

三维点云的地面分割目标是将每个点指定为属于地面点或不属于地面点。在这项工作中，地面分割是通过执行高斯过程回归来实现的。在地形建模的情况下，GPs是非参数工具，可以用来学习地面地形的模型。为了更深入地探索GPs在地面建模中的应用，读者可以参考Vasudevan等人的工作[11]。在这项工作中，应用了[15]中描述的近似GP回归方法。图1中给出了典型激光扫描的地面分割结果示例。

定义接受一组径向bins$S_Y$并返回非地面点$Y^{{}^{\prime }}$的函数为$Y^{{}^{\prime }}\subset Y=\chi (S_Y)$

对非地面点进行聚类

一旦地面点已经被分割，剩余的非地面点必须被聚类，以便应用SGC-NDT算法，这是使用贪婪聚类技术实现的。对于扫描$Y$，定义一个聚类$\omega \subset Y$，以及集合为 Ω Y = { ω 1 , . . . , ω N Ω } \Omega_{Y} = \{ \omega_1,..., \omega_{N_{\Omega}} \} ΩY​={ω1​,...,ωNΩ​​}，其中$N_{\Omega }$是聚类的总数，最初是未知的。这些聚类是通过首先从均匀分布$\mathcal{U}$中随机采样一个初始的bin${\tilde{s}}_i^j\in S_Y$生成的的，满足${\tilde{s}}_i^j\sim \mathcal{U}(S_Y)$。请注意，$S_Y$是由3D雷达扫描中非地面点的径向bin构成的。定义最近邻函数${\Theta }_{S_Y}$，它返回来自${\tilde{s}}_i^J$的八个相邻bin的集合 { s ~ i + p j + q } ∖ s ~ i j , p ∈ { − 1 , 0 , 1 } , q ∈ { − 1 , 0 , 1 } \{\tilde{s}_{i+p}^{j+q}\}\setminus \tilde{s}_i^j, p \in \{-1,0,1\},q \in \{-1,0,1\} {s~i+pj+q​}∖s~ij​,p∈{−1,0,1},q∈{−1,0,1}。

${\tilde{s}}_i^j$的最近邻居生成并添加到最近邻居bin的有序列表$Q_{nn}$中。可以将$Q_{nn}$中一个bin与${\tilde{s}}_i^j$进行比较，以确定两者是否可以合并。使用$\Phi ({\tilde{s}}_i^j,Q_{nn}^k)$函数来决定是否合并bin、其中 Φ ： S Y × S Y → { 0 , 1 } \Phi：S_Y \times S_Y \to \{0,1\} Φ：SY​×SY​→{0,1}以及$Q_{nn}^k$是$Q_{nn}$列表的第$k$个元素。如果两个bin可以被合并则函数$\Phi$返回1，否则返回0。在$\Phi$函数中，不同的度量可以用来比较点集bin，例如bin中包含的点的平均值之间的欧几里得距离，每个bin内高斯分布之间的$L_2$距离，或者高斯拟合的测试。如果这些bin可以被组合，则邻居bin被添加到bin的开放列表${\mathcal{Q}}_o$中。邻居bin也被从所有bin的集合$S_Y$中移除，并被添加到当前聚类$C_{cur}$中。探索和评估了来自$Q_o$中bin最近的邻居。当一个bin被探索时，它最近的邻居也会根据评估函数$\Phi$被添加到$Q_o$中。一旦$Q_o$为空，这意味着没有其他的最近邻居可以被分配到当前的聚类中，所以从$S_Y$中选取一个新的bin，并且重复该过程。整个过程一直持续到将$S_Y$中的所有bin配给一个聚类。贪婪聚类完成后的高斯分布示例如图2所示。

定义接受非地面点$Y^{\prime }$并返回集聚类集合${\Omega }_Y$的函数，${\Omega }_Y=\beta (Y^{{}^{\prime }})$。

正态分布变换

正态分布变换是一种方法，通过这种方法，点云的各个部分被映射并表示为栅格结构中的高斯分布。NDT配准算法首先将参考扫描占据的空间细分为一组栅格单元$c$。定义在栅格$c_i$中的参考扫描中的点的集合为 Y c i = { y 1 c i , . . . , y N c i c i } Y^{c_i} = \{ y_1^{c_i},...,y_{N_{c_i}}^{c_i} \} Yci​={y1ci​​,...,yNci​​ci​​}满足 y k c i ∈ c i , k ∈ { 1 , . . . , N c i } y_k^{c_i} \in c_i, k \in \{ 1,...,N_{c_i} \} ykci​​∈ci​,k∈{1,...,Nci​​}。每个栅格$c_i$内的点分布被建模为具有平均值${\mu }_{c_i}$和协方差矩阵${\Sigma }_{c_i}$的高斯分布。高斯分布代表一个生成过程，他建模了栅格内点$Y^{c_i}$的局部表面。

由于点云是由高斯分布的分段连续和分段可微的高斯求和来建模的，因此可以使用数值优化工具来将场景扫描与参考扫描进行配准。可以计算适应度代价$\Lambda ：{\mathbb{R}}^3\times \mathbb{S}\mathbb{O}(3)\to \mathbb{R}$，它量化了扫描$X$和$Y$之间重叠的度量。Magnusson最初的工作是通过评估变换后扫描中的每个点对应于它所占据的NDT栅格的分布来计算代价[16]。每个点的得分贡献如下
$$\rho (y)=exp(-\frac{(y-{\mu }_{c_i}{)}^T{\Sigma }_{c_i}^{-1}(y-{\mu }_{c_i})}{2})$$
其中${\mu }_{c_i}$和${\Sigma }_{c_i}$是样本均值和协方差。扫描中所有点的得分分量之和称为NDT点到分布(p2d)的代价，给出如下
$$\Lambda (p)=-\sum _{k=1}^{N_x}{\rho }_Y(T(p,x_k))$$

Stoyanov等人提出课NDT的一个修改版本，它生成了两个扫描的NDT表示，然后比较扫描的分布，以便对齐它们[7]。分布到分布代价函数评估场景和参考扫描的所有成对高斯分布。然而，在Stoyanov的工作中，代价函数只在最近的高斯分量上评估以减少计算量，这导致总代价函数的不连续，因为当平均点之间的对应关系改变时，梯度和海塞矩阵不存在于变换空间中。当场景扫描点跨越栅格单元边界时，代价函数的不连续性也存在于点到分布NDT中。Magnusson等人利用三线性插值方案[17]缓解了代价函数不连续的问题，然而，插值并不能完全解决这个问题，因为代价函数仍然是不连续的。

应该注意的是，两个NDT代价函数都有可用于计算梯度${\eta }_g$和海塞矩阵${\eta }_H$的分析表达式。对于点到分布匹配，定义函数${\rho }_g(x_k,p)$和${\rho }_H(x,p)$，它们使用场景扫描中的一个点和变换参数来计算点$x_k$的相关梯度和海塞矩阵的贡献。优化从参数估计$p_0$开始，一旦梯度的范数小于用户指定的阈值$||{\eta }_g||\in \mathbb{R}$，优化就终止。Stoyanov用线搜索的拟牛顿法求解优化问题[7]，但是也可以使用其他方法，如Broyden-Fletcher-Goldfarb-Shanno(BFGS)更新方法。

分割贪婪聚类

使用由贪婪聚类生成的高斯分布，修改NDT算法以使用所有高斯分布来评估代价函数。算法1中给出了SGC-NDT-P2D的总结。

对于SGC-NDT-D2D，应用了类似于P2D版本的方法，除了在D2D的情况下，两个激光扫描都被分割和聚类，并且比较每个扫描的结果高斯分布集合以执行配准。

实验结果

SGC-NDT方法使用不同环境的两个数据集进行评估，并与其他扫描配准算法进行比较。用于比较的算法有ICP、NDT和G-ICP。出于比较的目的，使用了ICP、NDT和G-ICP的点云库(PCL)实现[18]。ICP算法使用$10m$的最大关联距离实现，NDT算法使用$3m$的栅格尺寸实现。对于所有基于优化的方法，当梯度的范数或步长的范数低于$10^{-6}$时，优化终止。

A. 户外城市环境中的精度

为了测试SGC-NDT相对于其他扫描配准方法的准确性，使用了福特校园视觉和LIDAR数据集[14]。数据集是使用Velodyne HDL-64E激光雷达生成的，地面真值是通过将Applanix POS-LV 420惯性导航系统产生的高质量速度和加速度测量结果与Trimble GPS相结合而获得的。当使用地面真值来对齐扫描时，可以看到对齐在方位上具有低于一度的精度，在位置上具有分米精度。每种算法使用激光雷达产生的每10个扫描进行成对扫描配准。用零平移和零旋转的参数估计初始化配准。然后将配准的平移和旋转误差与真实测量值进行比较。平移和旋转误差分布如图3所示。

应该注意的是，箱线图的上下相邻的白边代表数据的1.5×四分位距范围。

图3中的误差分布表明，与地面真值相比，SGC-NDT算法和G-ICP算法都能产生准确的结果。NDT的大平移误差分布表明算法的收敛性差，因为优化有收敛到局部极小值的趋势。ICP算法也显示出相当低的平移和旋转误差，然而，似乎不如SGC-NDT或G-ICP精确。

为了进一步评估扫描配准质量，成对配准的扫描被聚集成全局地图。使用清晰度测量对地图进行评估，它也被用于[10]中的地图评估。通过将三维空间离散成体素栅格，并记录占据的体素数量，来评估地图的清晰度。对于实验，使用$0.1m$的体素尺寸。一张评估为较低数量的地图被认为比评估为较高数量的地图更清晰。直观地说，清晰度质量测量捕捉到随着扫描的聚集，由渐进的成对配准误差引起的地图模糊。清晰度测量用于SGC-NDT、ICP和G-ICP。NDT的清晰度没有被评估，因为在许多情况下，配准没有收敛到全局最小值。表一列出了SGC-NDT、ICP和G-ICP的清晰度度量。

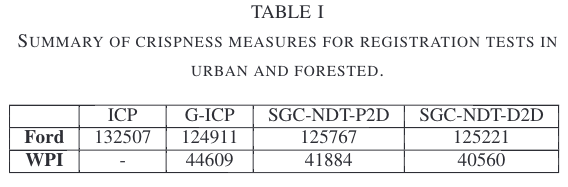
清晰度度量表明，SGC-NDT算法和G-ICP算法都能生成高质量的地图，而由于配准误差的累积，ICP生成的地图质量较低。

B.稀疏森林中环境中的准确性

为了确定所提出方法的鲁棒性，使用从一个稀疏森林环境中收集的数据集进行了实验。这些数据是作为WPI“NASA 采样返回机器人挑战赛”的一部分收集的。激光扫描是通过Velodyne HDL-32E激光雷达收集的，激光雷达安装在为迎接挑战而定制的底盘上。环境主要由树木和其他树叶以及一个小凉亭组成。森林环境对于配准来说特别具有挑战性，因为树叶、草地和灌木丛往往会产生不规则的、有噪声的点云，并带有模糊的局部表面，导致难以确定正确的点对应关系和准确的表面法线信息。

为了确定所有类型环境的鲁棒性，只给出了之前城市场景实验中表现最好的两种算法，SGC-NDT和G-ICP，因为ICP和NDT算法不能一致地收敛，也不能提供任何有意义的总体比较结果。该实验以类似于城市场景实验的方式进行，其中使用竞争的算法成对配准扫描。配准的扫描然后被聚集成一个全局地图。当机器人在环境中缓慢移动时，每一种算法都使用激光雷达产生的每50个扫描进行成对扫描配准。用零平移和零旋转的参数估计初始化。从视觉上看，图4显示了配准的汇总结果。

该实验证明了里程计估计高度不准确的情况下的性能，例如在GPS拒绝的环境中，或者在车轮打滑或其他因素使准确的状态估计变得困难的车辆上。由于WPI数据集无法获得准确的地面真值，因此仅根据清晰度度量来评估全局地图。WPI数据集的清晰度度量见表一。

清晰度测量表明，与SGC-NDT算法相比，G-ICP不能提供准确的扫描配准结果。收敛的困难很可能是因为G-ICP依赖于精确的表面法线来确定正确的点对应关系，这在森林环境中很难实现。SRG-NDT算法将树木和灌木等环境特征建模为高斯分布的混合，因此在局部表面结构较差的稀疏环境中可以获得良好的配准结果。图4显示了穿越区域自上而下的地图，以及环境特征的特写视图。G-ICP地图显示了很大的漂移，有时错误地收敛到局部极小值，而SGC-NDT地图保持了非常清晰的特征。通过检查特写视图中结构柱的对齐情况，可以清楚地识别特征的清晰程度。

结论

这项工作提出了分割贪婪聚类NDT，一个修改版本的NDT算法。所提出的方法从扫描中分割地面，使用贪婪聚类算法对非地面点进行聚类，并将每个聚类建模为高斯分布。NDT扫描配准算法被修改为使用聚类后的高斯分布，与标准NDT算法相反，标准NDT算法是从体素栅格生成高斯聚类。SGC-NDT方法既适用于点对点NDT，也适用于分布对分布NDT，并在城市和稀疏的森林环境中显示出良好的结果。未来的工作包括使用高斯聚类作为扫描初始对齐的特征，优化实时应用的实现，全面分析计算复杂性，以及在更大的环境下评估算法。

总结以下：三个亮点：1.地面分割，这个确实是相当有用的，尤其是在森林场景中。2.贪婪聚类算法，也就是下一篇论文中的区域生长聚类，也可以理解为简化版的DBSCAN聚类，解决了固定尺寸栅格聚类导致的计算复杂性高和无法建模较大的自然特征的问题。3.使用所有的聚类生成的高斯分布来评估代价函数，实现了代价函数在整个变换参数空间上的连续和可导性质，保证了收敛性，同时由于第二点的存在，在计算效率上也可以保证。