本文主要是介绍简述最小二乘法基本概念和拟合方法,给出高次函数的拟合公式,配有有matlab仿真程序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
最小二乘法是一种常用的曲线拟合算法,尤其对于存在白噪声的数据的拟合尤其有用。本文首先简析最小二乘法的作用,然后再推到高次(以3次为例)多项式的拟合公式,并用MATLAB仿真展示具体的应用示例。
一、最小二乘法的用途
最小二乘法是一种常用的曲线拟合算法,尤其对于存在白噪声的数据的拟合尤其有用。有效估计就是具有最小方差的估计,最小二乘法是一种对于物理量参数的有效估计,这种方法综合考虑所有点的偏差,所评估的参数使得对于所有的测量点方差最小。
二、高次多项式的拟合公式推导
假设需要使用最小二乘法对一个3次函数进行拟合,该函数的真值表达式如下:
在实际应用中,作为输入,在测量输出
时,往往会引入白噪声
,这样实际在测量数据时表达式变为:
现在给定一组输入值,会得到含有白噪声的一组测量值
,由输入值
和测量值
,使用最小二乘法对
四个参数进行估计。
根据最小二乘法的定义,使得
为最小。
为此,需要分别对四个参数求偏导数,并令其为0,即可得到一个线性方程组,如下:
对以上四个线性方程整理可得:
写成矩阵的形式可得:
令
可简化写成,,于是可得估计参数如下:
三、Matlab代码仿真
根据上面推导的公式,对一个3次函数进行参数辨识,以证明该公式的有效性。
需要辨识的三次函数如下:
辨识时对该三次函数加入10*[-0.5,0.5]范围的白噪声。matlab代码实现如下:
clc
clear
close all
X_6_sum=0;X_5_sum=0;X_4_sum=0;X_3_sum=0;X_2_sum=0;X_1_sum=0;
RX_3_sum=0;RX_2_sum=0;RX_1_sum=0;
R_sum=0;N=0;
X=-10:0.01:10;
Y=X;
for count=1:length(X)Y(count)=0.5*X(count)^3+1.2*X(count)^2+2*X(count)+5+10*(rand()-0.5);X_6_sum=X_6_sum+X(count)^6;X_5_sum=X_5_sum+X(count)^5;X_4_sum=X_4_sum+X(count)^4;X_3_sum=X_3_sum+X(count)^3;X_2_sum=X_2_sum+X(count)^2;X_1_sum=X_1_sum+X(count);N=length(X);RX_3_sum=RX_3_sum+Y(count)*X(count)^3;RX_2_sum=RX_2_sum+Y(count)*X(count)^2;RX_1_sum=RX_1_sum+Y(count)*X(count);R_sum=R_sum+Y(count);
end
plot(X,Y,'b.','MarkerSize',10);
A=[X_6_sum,X_5_sum,X_4_sum,X_3_sum;X_5_sum,X_4_sum,X_3_sum,X_2_sum;X_4_sum,X_3_sum,X_2_sum,X_1_sum;X_3_sum,X_2_sum,X_1_sum,N];
C=[RX_3_sum;RX_2_sum;RX_1_sum;R_sum];
B=inv(A)*C
B1=polyfit(X,Y,3)
Y1=B(1).*X.^3+B(2).*X.^2+B(3).*X+B(4);
hold on
plot(X,Y1,'r','MarkerSize',10);仿真结果如下:
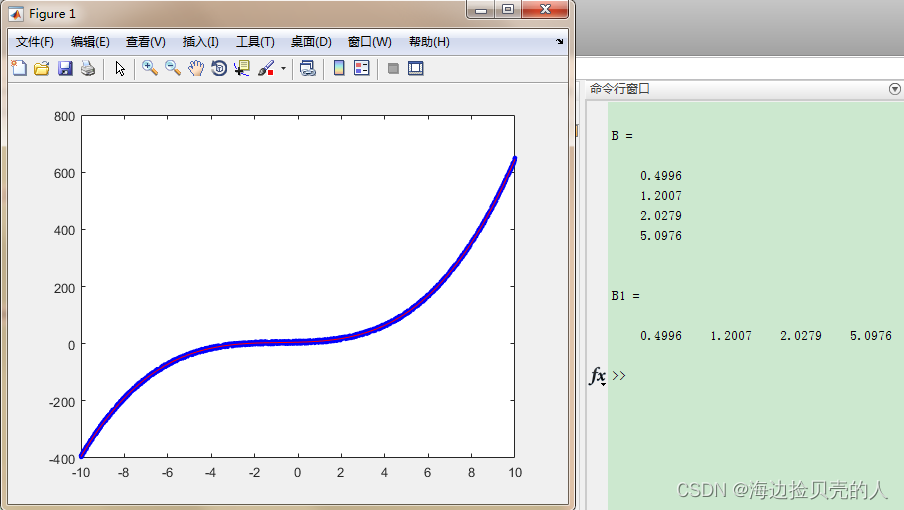
其中B为采用上述公式得到的拟合结果,B1为采用matlab自带的函数进行的拟合得到的结果,两者对比可证明结果是一致的,并且和设定的真实参数相差很小,从而证明该公式的正确性。
这篇关于简述最小二乘法基本概念和拟合方法,给出高次函数的拟合公式,配有有matlab仿真程序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






