神经元、神经网络和线性判别

本文主要是介绍神经元、神经网络和线性判别，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考《机械工业出版社的matlab》与《机器学习与机器学习算法视角》

Hebb法则

Hebb法则认为突触链接强度的变化与两个相连神经元激活的相关性成正比。如果两个神经元始终同时激活，那么他们之间连接的强度会变大。反之，如果两个神经元从不同时激活，它们之间的连接就会消失。是经典的条件发射（铃声与狗分泌唾液的实验）。当神经元同时被激活时，他们之间的连接会被增强，这种效应也被称为长时程增强效应和神经可塑性。

McCulloch和Pitts神经元

神经元的一种模型
模型包含如下部分：
1.一组输入加权ω_i相当于突触
2.一个加法器把输入信号相加（与收集电荷的细胞膜等价）
3.一个激活函数（最初是一个阈值函数）决定新报对于当前的输入是否激活（放电）。
McCulloch和Pitts神经元使用的是二元的阈值函数，把所有输入按权相加，结果超过阈值则判断为1，否则为0。这里的权重可正可负，等价于实际神经元的兴奋性和抑制性。
与现实神经元相比，这样的模型只能进行线性的计算，无法进行非线性的计算；只能给出单一的脉冲响应，实际的神经元可给出一个电位序列；实际神经元的兴奋性抑制性是无法转变的；且实际神经元通常存在反馈机制。

神经网络

单个神经元只能在提供输入后显现激活或不激活，单个神经元是不具备学习能力的。然而将一系列神经元放置在一起，形成神经网络的时候，则能做一些事情。
书里这一段思考十分值得一读，这里摘出来：
首先，我们要思考一个问题，如何使神经元能够学习。在线面几章中，我们将要研究监督学习，意思是算法将用过样例来学习：在学习数据集中，每一个数据点都有一个正确的输出值与之对应。乍一看，似乎毫无意义，既然你已经知道了正确答案，为什么还要去学习呢？这里的关键在于1.2节提到的泛化的概念。假设数据中存在某一种模式，通过给神经网络一些已知的样例，我们希望能够发现这种模式，并且正确地预测其他样例。这有时称为模式识别。
我们之前了解了McCulloch和Pitts神经元模型，它除了上面所说的三部分外并没有其他内容，将视野从单个神经元扩大到整个神经网络，神经元之间也存在联系。学习是发生在神经元与神经元之间的。我们应该如何改变神经元的权重和阈值，使网络能够频繁地得到正确的结果？

感知器

感知器是历史上第一个神经网络，是McCulloch和Pitts神经元组成的集合。
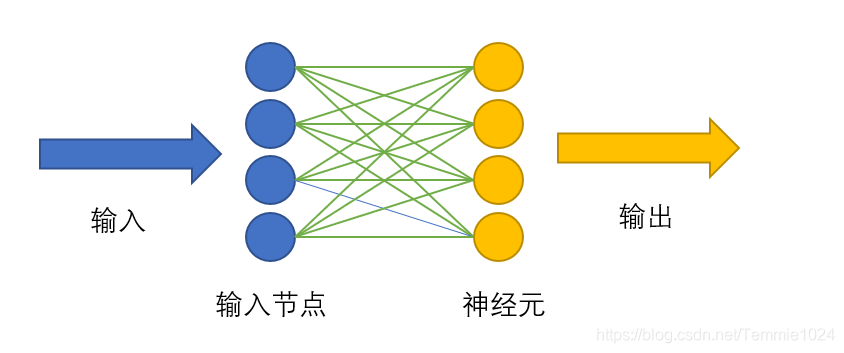
在这里插入图片描述
图中是一个示意图，实际上神经元和输入节点数量未必对等。
在学习时，对于给定的输入，得到一个包含激活和不激活的神经元模式。输入节点到神经元之间存在权重ω_iji表示节点，j表示神经元，这就指向了节点与神经元连接的关系。这里，权重的设置就是关键了。
当得到一个错误结果的时候，我们需要选中输出错误结果的神经元并找到与其相连的节点及其权重。我们需要调整这些关联的权重。如果错误的神经元不该激活，那么权重应该调小，反之如果应该激活，那么权重应该调大。
学习速率η权重调整的幅度幅度过大会导致网络不稳定，过小会较大幅度增大学习时间，但也会降低系统对噪音的敏感度。一般η取值在0.1-04之间。如果设置为1，则不会影响学习效率。
输入偏置输入偏置用于解决0输入时，某些神经元需要激活，因为在输入为0时，无论0乘以什么都为零，理论上是无法激活的，因此使用偏置来让它从一个值开始变化，这样0输入就不是一个0值了。
线性可分性： 感知器将神经元该不该激活的情况分开。它尝试寻找一条直线，对于三维是平面，更高维为超平面。在线（面）的一边神经元是激活的，另一侧是未激活的。这个边界为决策边界（判别函数）。当给定一些数据，以及与之对应的目标输出时候，感知器只是尝试寻找一条直线，使能够把神经元激活的样例和神经元不激活的样例区分开。如果这样的直线存在就称为线性可分。