本文主要是介绍深度学习(生成式模型)——DDIM:Denoising Diffusion Implicit Models,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 前言
- 为什么DDPM的反向过程与前向过程步数绑定
- DDIM如何减少DDPM反向过程步数
- DDIM的优化目标
- DDIM的训练与测试
前言
上一篇博文介绍了DDIM的前身DDPM。DDPM的反向过程与前向过程步数一一对应,例如前向过程有1000步,那么反向过程也需要有1000步,这导致DDPM生成图像的效率非常缓慢。本文介绍的DDIM将降低反向过程的推断步数,从而提高生成图像的效率。
值得一提的是,DDIM的反向过程仍然是马尔可夫链,但论文里有讨论非马尔可夫链的生成模型。本博文只总结DDIM如何提高DDPM的生成图像效率。
为什么DDPM的反向过程与前向过程步数绑定
DDPM反向过程的推导公式为
q ( x ^ t − 1 ∣ x ^ t ) = q ( x ^ t − 1 ∣ x ^ t , x ^ 0 ) = q ( x ^ t − 1 , x ^ t , x ^ 0 ) q ( x ^ t , x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 , x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) q ( x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) q ( x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 , x ^ 0 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) = q ( x ^ t ∣ x ^ t − 1 ) q ( x ^ t − 1 ∣ x ^ 0 ) q ( x ^ t ∣ x ^ 0 ) \begin{aligned} q(\hat x_{t-1}|\hat x_{t})&=q(\hat x_{t-1}|\hat x_{t},\hat x_0)\\ &=\frac{q(\hat x_{t-1},\hat x_t,\hat x_0)}{q(\hat x_t,\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1},\hat x_0)}{q(\hat x_t|\hat x_0)q(\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1}|\hat x_0)q(\hat x_0)}{q(\hat x_t|\hat x_0)q(\hat x_0)}\\ &=\frac{q(\hat x_{t}|\hat x_{t-1},\hat x_0)q(\hat x_{t-1}|\hat x_0)}{q(\hat x_t|\hat x_0)}\\ &=\frac{ q(\hat x_{t}|\hat x_{t-1})q(\hat x_{t-1}|\hat x_0)}{q(\hat x_t|\hat x_0)} \end{aligned} q(x^t−1∣x^t)=q(x^t−1∣x^t,x^0)=q(x^t,x^0)q(x^t−1,x^t,x^0)=q(x^t∣x^0)q(x^0)q(x^t∣x^t−1,x^0)q(x^t−1,x^0)=q(x^t∣x^0)q(x^0)q(x^t∣x^t−1,x^0)q(x^t−1∣x^0)q(x^0)=q(x^t∣x^0)q(x^t∣x^t−1,x^0)q(x^t−1∣x^0)=q(x^t∣x^0)q(x^t∣x^t−1)q(x^t−1∣x^0)
值得一提的是,反向过程的马尔可夫状态 x ^ t \hat x_t x^t、 x ^ t − 1 \hat x_{t-1} x^t−1不一定要与前向过程一致,如下图所示,反向过程的状态 x ^ T \hat x_T x^T、 x ^ T − 1 \hat x_{T-1} x^T−1对应前向过程的 x T x_T xT、 x T − 2 x_{T-2} xT−2。

从上述公式构成来看,反向过程的概率图形式与 q ( x ^ t ∣ x ^ t − 1 ) q(\hat x_t|\hat x_{t-1}) q(x^t∣x^t−1)有关。而在DDPM中, q ( x ^ t ∣ x ^ t − 1 ) q(\hat x_t|\hat x_{t-1}) q(x^t∣x^t−1)与前向过程 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1)一致,这就导致DDPM的概率图为

因此利用DDPM推导的 q ( x ^ t − 1 ∣ x ^ t ) q(\hat x_{t-1}|\hat x_{t}) q(x^t−1∣x^t)进行反向过程时,状态转移步数必须与前向过程一致。
DDIM如何减少DDPM反向过程步数
在上一节中,我们说明了反向过程的马尔可夫状态与前向过程不需要一致,这表明 q ( x ^ t − 1 ∣ x ^ t ) q(\hat x_{t-1}|\hat x_{t}) q(x^t−1∣x^t)的概率密度函数有多种。找到合适的概率密度函数,我们即可减少反向过程的迭代步数,同时保持生成图像的质量,这便是DDIM的出发点。以下的推导中,我们将用 x t 、 x t − 1 x_t、x_{t-1} xt、xt−1来表示反向过程的马尔可夫状态。
本章节的所有符号定义与深度学习(生成式模型)——DDPM:denoising diffusion probabilistic models一致
为了书写方便,除非特殊提及,在以下的所有推导中,所有的 x x x、 ϵ \epsilon ϵ符号都表示随机变量,而不是一个样本。
在DDPM的前向过程里有
x t − 1 = α ˉ t x 0 + 1 − α ˉ t ϵ t − 1 (2.0) \begin{aligned} x_{t-1}&=\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_{t-1}\tag{2.0} \end{aligned} xt−1=αˉtx0+1−αˉtϵt−1(2.0)
已知两个均值为0的高斯分布相加具备以下性质
N ( 0 , δ 1 2 ) + N ( 0 , δ 2 2 ) = N ( 0 , δ 1 2 + δ 2 2 ) \mathcal N(0,\delta_1^2)+\mathcal N(0,\delta_2^2)=\mathcal N(0,\delta_1^2+\delta_2^2) N(0,δ12)+N(0,δ22)=N(0,δ12+δ22)
依据重参数化技巧,已知
1 − α ˉ t − δ t 2 ϵ t ∼ N ( 0 , 1 − α ˉ t − δ t 2 ) δ t ϵ ∼ N ( 0 , δ t 2 ) 1 − α ˉ ϵ t − 1 ∼ N ( 0 , 1 − α ˉ t − 1 ) \begin{aligned} \sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_{t}&\sim \mathcal N(0,1-\bar\alpha_{t}-\delta_t^2)\\ \delta_t\epsilon&\sim \mathcal N(0,\delta_t^2)\\ \sqrt{1-\bar\alpha}\epsilon_{t-1}&\sim \mathcal N(0,1-\bar \alpha_{t-1}) \end{aligned} 1−αˉt−δt2ϵtδtϵ1−αˉϵt−1∼N(0,1−αˉt−δt2)∼N(0,δt2)∼N(0,1−αˉt−1)
则有
x t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t ϵ t − 1 = α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ t + δ t ϵ = α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 x t − α ˉ t x 0 1 − α ˉ t + δ t ϵ (2.1) \begin{aligned} x_{t-1}&=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_t}\epsilon_{t-1}\\ &=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_{t}+\delta_t\epsilon\\ &=\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\frac{x_t-\sqrt{\bar \alpha_t}x_0}{\sqrt{1-\bar\alpha_t}}+\delta_t\epsilon \end{aligned}\tag{2.1} xt−1=αˉt−1x0+1−αˉtϵt−1=αˉt−1x0+1−αˉt−δt2ϵt+δtϵ=αˉt−1x0+1−αˉt−δt21−αˉtxt−αˉtx0+δtϵ(2.1)
依据重参数化公式,式2.1可表征为
q ( x t − 1 ∣ x t ) = q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 x t − α ˉ t x 0 1 − α ˉ t , δ t 2 I ) (2.2) \begin{aligned} q(x_{t-1}|x_{t})&=q(x_{t-1}|x_t,x_0)\\ &=\mathcal N(x_{t-1};\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\frac{x_t-\sqrt{\bar \alpha_t}x_0}{\sqrt{1-\bar\alpha_t}},\delta_t^2\mathcal I)\tag{2.2} \end{aligned} q(xt−1∣xt)=q(xt−1∣xt,x0)=N(xt−1;αˉt−1x0+1−αˉt−δt21−αˉtxt−αˉtx0,δt2I)(2.2)
注意式2.2的推导过程绕过了贝叶斯公式,而且没有指定反向过程的状态转移图,因此式2.1是一个反向过程的概率密度函数族,不同的 δ t \delta_t δt表示不同的概率密度函数,对应反向过程不同的马尔可夫状态转移链。
结合式2.0,式2.2可进一步变化为
q ( x t − 1 ∣ x t ) = q ( x t − 1 ∣ x t , x 0 ) = N ( x t − 1 ; α ˉ t − 1 x t − 1 − α ˉ t ϵ t α ˉ t + 1 − α ˉ t − δ t 2 ϵ t , δ t 2 I ) (2.3) \begin{aligned} q(x_{t-1}|x_t)&=q(x_{t-1}|x_t,x_0)\\ &=N(x_{t-1};\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}\epsilon_t}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_t,\delta_t^2\mathcal I)\tag{2.3} \end{aligned} q(xt−1∣xt)=q(xt−1∣xt,x0)=N(xt−1;αˉt−1αˉtxt−1−αˉtϵt+1−αˉt−δt2ϵt,δt2I)(2.3)
DDIM的优化目标
由于DDIM与DDPM一样,前向过程与反向过程均为马尔科夫链,因此优化目标也一致。从上一篇博客,我们可知DDPM的优化目标为
L = ∑ t = 2 T D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) = ∑ t = 2 T ( 1 2 ( n + 1 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 − n + l o g 1 ) = ∑ t = 2 T ( 1 2 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 ) \begin{aligned} L&=\sum_{t=2}^TD_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))\\ &=\sum_{t=2}^T(\frac{1}{2}(n+\frac{1}{\delta_t^2}||\mu_t-\mu_\theta||^2-n+log1)\\ &=\sum_{t=2}^T(\frac{1}{2\delta_t^2}||\mu_t-\mu_\theta||^2)\\ \end{aligned} L=t=2∑TDKL(q(xt−1∣xt,x0)∣∣pθ(xt−1∣xt))=t=2∑T(21(n+δt21∣∣μt−μθ∣∣2−n+log1)=t=2∑T(2δt21∣∣μt−μθ∣∣2)
设网络预测的噪声为 ϵ θ ( x t ) \epsilon_\theta(x_t) ϵθ(xt),则DDIM的优化目标为:
L = ∑ t = 2 T ( 1 2 δ t 2 ∣ ∣ μ t − μ θ ∣ ∣ 2 ) = ∑ t = 2 T ( 1 2 δ 2 ∣ ∣ α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ t − ( α ˉ t − 1 x 0 + 1 − α ˉ t − δ t 2 ϵ θ ( x t ) ) ∣ ∣ 2 ) = ∑ t = 2 T ( 1 − α ˉ t − δ t 2 2 δ t 2 ∣ ∣ ϵ t − ϵ θ ( x t ) ∣ ∣ 2 ) \begin{aligned} L&=\sum_{t=2}^T(\frac{1}{2\delta_t^2}||\mu_t-\mu_\theta||^2)\\ &=\sum_{t=2}^T(\frac{1}{2\delta^2}||\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_t-(\sqrt{\bar \alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_\theta(x_t))||^2)\\ &=\sum_{t=2}^T(\frac{1-\bar\alpha_t-\delta_t^2}{2\delta_t^2}||\epsilon_t-\epsilon_{\theta}(x_t)||^2) \end{aligned} L=t=2∑T(2δt21∣∣μt−μθ∣∣2)=t=2∑T(2δ21∣∣αˉt−1x0+1−αˉt−δt2ϵt−(αˉt−1x0+1−αˉt−δt2ϵθ(xt))∣∣2)=t=2∑T(2δt21−αˉt−δt2∣∣ϵt−ϵθ(xt)∣∣2)
结合上式以及坐标下降法,可得DDIM最终优化目标 L L L为
L = ∣ ∣ ϵ t − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ t ) ∣ ∣ 2 L=||\epsilon_t-\epsilon_\theta(\sqrt{\bar \alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon_t)||^2 L=∣∣ϵt−ϵθ(αˉtx0+1−αˉtϵt)∣∣2
与DDPM一致
DDIM的训练与测试
DDIM的训练过程与DDPM一致,反向过程的采样公式变为
x t − 1 = α ˉ t − 1 x t − 1 − α ˉ t ϵ θ ( x t ) α ˉ t + 1 − α ˉ t − δ t 2 ϵ θ ( x t ) + δ t ϵ (4.0) x_{t-1}=\sqrt{\bar \alpha_{t-1}}\frac{x_t-\sqrt{1-\bar \alpha_t}\epsilon_\theta(x_t)}{\sqrt{\bar\alpha_t}}+\sqrt{1-\bar\alpha_{t}-\delta_t^2}\epsilon_\theta(x_t)+\delta_t\epsilon\tag{4.0} xt−1=αˉt−1αˉtxt−1−αˉtϵθ(xt)+1−αˉt−δt2ϵθ(xt)+δtϵ(4.0)
其中 ϵ \epsilon ϵ从标准正态分布中采样得到, δ t \delta_t δt为超参数,其取值为
δ t = η ( 1 − α ˉ t − 1 ) / ( 1 − α ˉ t ) 1 − α ˉ t / α ˉ t − 1 \delta_t=\eta\sqrt{(1-\bar\alpha_{t-1})/(1-\bar\alpha_{t})}\sqrt{1-\bar\alpha_t/\bar\alpha_{t-1}} δt=η(1−αˉt−1)/(1−αˉt)1−αˉt/αˉt−1
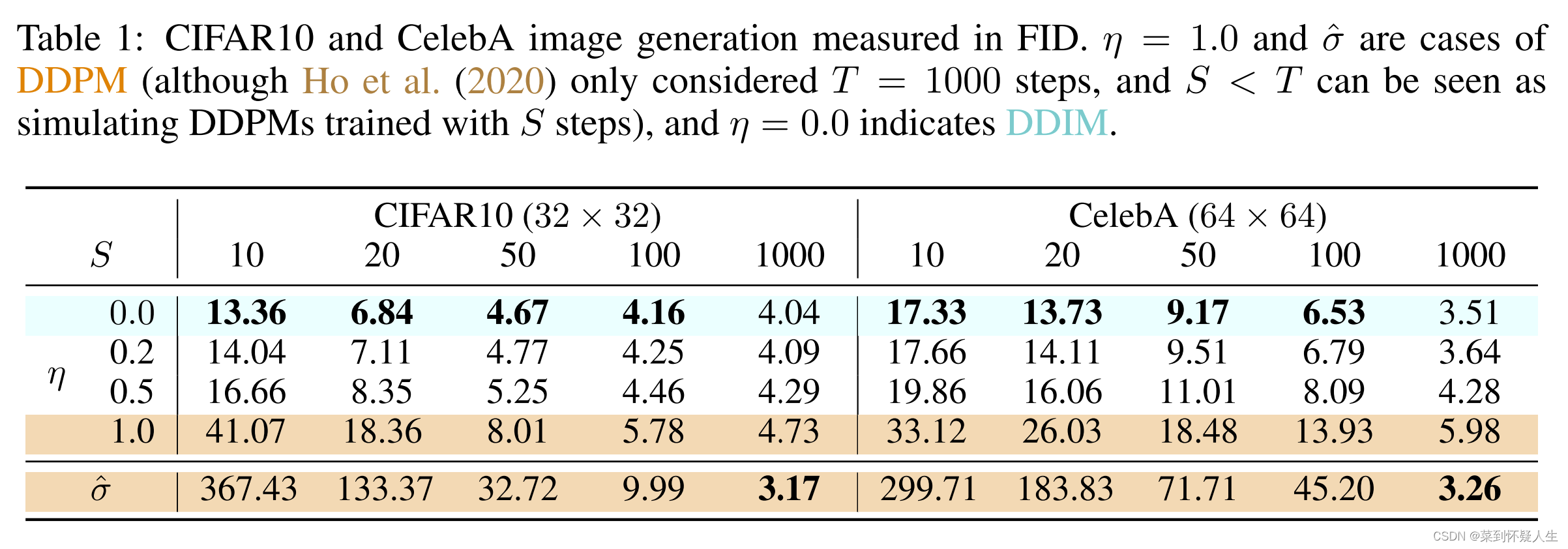
特别的,当 η = 1 \eta=1 η=1时,DDIM的反向过程与DDPM一致。当 η = 0 \eta=0 η=0时,式4.0的 ϵ \epsilon ϵ将被去掉,从而不具备随机性。即反向过程步数固定情况下,从一个噪声生成的图片将是确定,DDIM一般将 η \eta η取值设为0。
具体的实验结果可见下图:
这篇关于深度学习(生成式模型)——DDIM:Denoising Diffusion Implicit Models的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



