本文主要是介绍C#,图论与图算法,有向图(Graph)之环(Cycle)判断的颜色算法与源代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
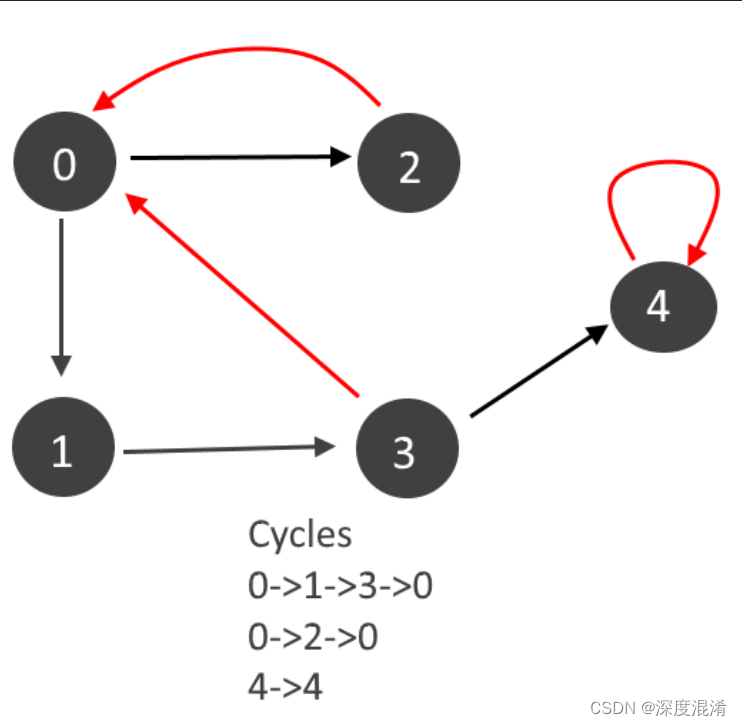
1 检查该图是否包含循环
给定一个有向图,检查该图是否包含循环。如果给定的图形至少包含一个循环,则函数应返回true,否则返回false。
方法:深度优先遍历可用于检测图中的循环。连接图的DFS生成树。只有当图中存在后缘时,图中才存在循环。后边是从节点到自身(自循环)或DFS生成的树中其祖先之一的边。在下图中,有3条后缘,用十字符号标记。可以观察到,这3条后缘表示图中存在3个循环。
对于断开连接的图,我们将DFS林作为输出。为了检测循环,我们可以通过检查后边缘来检查各个树中的循环。
图像来源:http://www.cs.yale.edu/homes/aspnes/pinewiki/DepthFirstSearch.html
在上一篇文章中,我们讨论了一个解决方案,该解决方案将访问的顶点存储在一个单独的数组中,该数组存储当前递归调用堆栈的顶点。
在这篇文章中,讨论了一种不同的解决方案。解决方案来自CLRS手册。其思想是对给定的图进行DFS,在进行遍历时,将以下三种颜色中的一种指定给每个顶点。
白色:尚未处理顶点。最初,所有顶点都是白色的。
灰色:正在处理顶点(此顶点的DFS已启动,但尚未完成,这意味着尚未处理此顶点的所有子体(在DFS树中)(或此顶点位于函数调用堆栈中)
这篇关于C#,图论与图算法,有向图(Graph)之环(Cycle)判断的颜色算法与源代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








