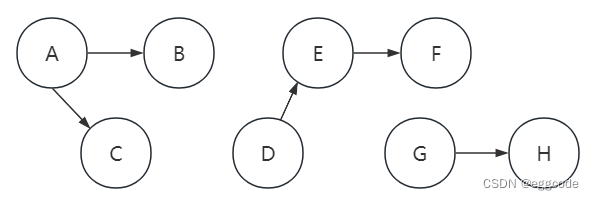
有向图专题

【HDU】3861 The King’s Problem 强连通缩点+有向图最小路径覆盖

传送门：【HDU】3861 The King’s Problem 题目分析：首先强连通缩点，因为形成一个环的王国肯定在一条路径中，这样才能保证拆的少。然后缩点后就是DAG图了，由于题目要求的是最小路径覆盖，那么二分匹配即可。代码如下： #include <cstdio>#include <cstring>#include <algorithm>#includ

图论求有向图的所有强连通分量 kosaraju算法

一、问题如何找到有向图（a）中的所有强连通分量，如图（b) 二、kosaraju算法 Kosaraju的算法（又称为–Sharir Kosaraju算法）是一个线性时间(linear time)算法找到的有向图的强连通分量。 1. 原理它利用了一个事实，逆图（与各边方向相同的图形反转, transpose graph）有相同的强连通分量的原始图。 2. 逆图

有向图的平方图算法分析与实现

有向图的平方图算法分析与实现 1. 使用邻接链表表示图2. 使用邻接矩阵表示图3.总结有向图的平方图（Graph Squaring）是一种图论中的操作，其目的是创建一个新图，其中如果原图中存在一条最多由两条边构成的路径从顶点u到顶点v，则在平方图中存在一条边(u, v)。本文将探讨如何通过邻接链表和邻接矩阵两种方式来表示有向图，并分别给出计算其平方图的算法，同时分析这些算法的时间

判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i≠j)

试基于图的深度优先搜索策略写一算法，判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i≠j)。注意：算法中涉及的图的基本操作必须在此存储结构上实现。图的邻接表以及相关类型和辅助变量定义如下： Status visited[MAX_VERTEX_NUM];typedef char VertexType;typedef struct ArcNode {int adj

有向图中打印所有的环路

转自：http://www.cnblogs.com/dugujiujian/archive/2011/08/19/2146042.html　最近项目中需要研究了一下有向图的环路问题。一个IT企业中有成千上万个应用，各个应用之间都是相互依赖的，一个用户请求进来后，会调用一系列应用，比如A调B、B调C、C调D等。这样所有的应用形成一个有向图，那么如果这个有向图中出现了环路，就悲剧了，用户的请求

判断一个有向图是否有环

转自：http://blog.csdn.net/panhe1992/article/details/8366466 Description 给出一个有向图，判断图中是否存在回路。 Input 第 1 行：输入图的顶点个数 N （ 1 ≤ N ≤ 2,500 ）和 C （图的边数， 1 ≤ C ≤ 6,200 ）；第 2 到 C+1 行中，第

【POJ3164】【有向图的最小生成树】【自己的模板】

Command Network Time Limit: 1000MS Memory Limit: 131072KTotal Submissions: 14811 Accepted: 4259 Description After a long lasting war on words, a war on arms finally breaks out between li

有向图的邻接表实现（Java版）

我是蚊子码农，欢饮您的关注。一、有向图介绍在无向图中，边没有方向性，就相当于一条公路，你可以来我这，我也可以去你那。然而，现实世界里，有一些通道是单向的，只允许一个方向通过。比如某些工作流程，你必须完成工作A，才能进行工作B。这时候，我们需要用有向边，来表达这些数据。当然，无向图可以看成特殊的有向图。二、有向图的表达（思考部分）我们知道，图是由结点集和边集构成的。其中，每一

HIHO #1182 : 欧拉路·三（有向图输出欧拉路径）

题目链接 A)建图是巧妙，使用边表示每一个数字，那么就是走完每一个边一次再回到起点，便是求欧拉回路 B)建图是有向图，建图需要注意，同时，输出的时候逆序输出 C)path保存的是完整的路径，输出的时候只需&1即可 #include<bits/stdc++.h>using namespace std;#define cl(a,b) memset(a,b,sizeof(a))#defin

有向图游戏 SG函数【博弈论】C++

SG函数可以用来判断在一个给定的有向图游戏中，当前局面的胜负状态。 SG函数的定义如下：设当前节点为v，那么SG(v)为当前局面的SG值。SG(v)的定义如下： - 如果当前节点v没有后继节点，则SG(v) = 0 - 如果当前节点v有若干个后继节点，分别为v1,v2,...,v_n，那么SG(v)为所有后继节点的SG值的异或和。即：SG(v) = SG(v1) XOR SG(v2) XOR

POJ 1847 Tram（Dijkstra单源有向图最短路径算法）

//Accepted 212 KB 0 ms C++ 1096 B 2013-02-27 19:42:55/*Sample Input3 2 12 2 32 3 12 1 2Sample Output0题意：给出N个站点，每个站点都有铁路通向其它的多个站点。如果当前要走的铁路是现在开关指向的铁路，则直接走即可，否则要手动扳动开关。难理解的可能是题意：直接指向的 w = 0, 需要

Day47 | 110.字符串接龙 105.有向图的完全可达性 106.岛屿的周长

110.字符串接龙 110. 字符串接龙题目题目描述字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列： 1. 序列中第一个字符串是 beginStr。 2. 序列中最后一个字符串是 endStr。 3. 每次转换只能改变一个字符。 4. 转换过程中的中间字符串必须是字典 strList 中的字符串，且strLis

代码随想录day53 110. 字符串接龙 105.有向图的完全可达性 106. 岛屿的周长

代码随想录day53 110. 字符串接龙 105.有向图的完全可达性 106. 岛屿的周长 110. 字符串接龙代码随想录 #include <iostream>#include <vector>#include <unordered_set>#include <unordered_map>#include <queue>using namespace std;int main(

代码随想录算法训练营第 53 天 |卡码网110.字符串接龙卡码网105.有向图的完全可达性卡码网106.岛屿的周长

代码随想录算法训练营 Day53 代码随想录算法训练营第 53 天 |卡码网110.字符串接龙卡码网105.有向图的完全可达性卡码网106.岛屿的周长目录代码随想录算法训练营前言卡码网110.字符串接龙卡码网105.有向图的完全可达性卡码网106.岛屿的周长一、卡码网110.字符串接龙1.题目链接2.思路3.题解二、105.有向图的完全可达性1.题目链接2.思路3.题解

10129 - Play on Words(欧拉道路有向图)

题目：10129 - Play on Words 题目大意：词语接龙。解题思路：刚开始没想到欧拉道路，直接找，结果超时了。这题满足要求的话就是把每个单词看做一条路，每条路连在一起走一遍就符合要求，欧拉回路也是符合要求的。满足欧拉道路：1，至多只有两个点的出度入度相差1。 2，这个有向图的无向图连通。（刚开始一直在想，如果有两条一样的路，这样怎么处理，后面

区分有向图和无向图：连通分量

连通图，只可能包含一个连通分量。若不连通才可能有多个连通分量区分有向图和无向图：连通分量 1.无向图：假设顶点3到顶点6有路径，称3和6是——连通的若图中任意两个点是连通的，则图为连通图，否则为不是连通图极大连通子图==连通分量 2.有向图：假设顶点3到顶点6有路径，顶点6到顶点3有路径，称3和6是——强连通的若图中任意两个点是强连通的，则图为

卡码网KamaCoder 105. 有向图的完全可达性

题目来源：105. 有向图的完全可达性 C++题解1： #include <iostream>#include <vector>#include <algorithm>using namespace std;int main(){int N, K;cin>>N>>K;// 如果边的数量不够，则一定不能到达所有点if(N-2 >= K) {cout<<-1; return 0;}// pat

C++ 有向图拓扑排序算法

代码 #include <algorithm>#include <cassert>#include <functional>#include <map>#include <memory>#include <queue>#include <set>#include <unordered_set>#include <vector>namespace jc {template <ty

算法训练营第六十七天 | 卡码网110 字符串接龙、卡码网105 有向图的完全可达性、卡码网106 岛屿的周长

卡码网110 字符串接龙这题一开始用的邻接表+dfs，不幸超时 #include <iostream>#include <list>#include <string>#include <vector>using namespace std;int minLen = 501;bool count(string a, string b) {int num = 0;for (int i

通俗范畴论2 有向图与准范畴

退一步海阔天空，在正式进入范畴论之前，我们可以重新审视一下我们是如何认识世界的，有了这个对人类认识世界过程的底层理解，可以帮助我们更好地理解范畴论。对于人类认识世界，最神奇的一点就是这个世界居然是可以认识的，我们可以用自然语言描述它、我们可以用数学公式表示它，当然我们也可以用二维的图画描摹它，我们也可以把它看成三维的空间加一维的时间，也可以将三维空间和时间看成一体的，从而我们的世界是四维时空。

有向图的强连通算法 -- tarjan算法

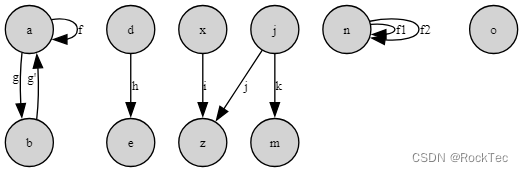
（画图什么真辛苦）强连通分量：在有向图 G 中，若两个顶点相互可达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。比如上面这幅图( a, b, e ), ( d, c, h ), ( f, g ) 分

有向图的负权值边与建模

参见 dijkstra 算法为什么高效昨天的文字最后提到 “经理办公桌上有一堆报表，让工人拟合一份最佳收支方案，工人用图论建模，就要使用 floyd，bellman-ford 算法。”，为什么工人的建模的熵减过程会出现负权重边，而自然的熵增过程不会出现负权重边，本文解释一二。自然的过程如爆炸，河水泛滥，昆虫无意识漫游等，这些都遵循第一性原理，而人为的过程比如金融投资，成本估算，道路交通网络

有向图最小环 floyd 和暴力bfs

Kessel Run locked by masonsbro ProblemSubmissionsLeaderboardDiscussionsEditorial

有向图强连通分量的Tarjan算法 [有向图强连通分量] 在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，

有向图强连通分量的Tarjan算法 [有向图强连通分量] 在有向图G中，如果两个顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。下图中，子图{1,2,3,4}为一个强连通分量，因为顶点

【QuikGraph】C#调用第三方库计算有向图、无向图的连通分量

QuikGraph库项目地址：https://github.com/KeRNeLith/QuikGraph 相关概念图论、连通分量、强连通分量相关概念，可以从其他博客中复习： https://blog.csdn.net/weixin_50564032/article/details/123289611 https://zhuanlan.zhihu.com/p/37792015 有向图计

hdu1269 有向图强连通分量 kosaraju 算法

迷宫城堡 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 4943 Accepted Submission(s): 2175 Problem Description 为了训练小希的方向感，Gardon建立了一座大城堡，里面有