本文主要是介绍通俗范畴论2 有向图与准范畴,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
退一步海阔天空,在正式进入范畴论之前,我们可以重新审视一下我们是如何认识世界的,有了这个对人类认识世界过程的底层理解,可以帮助我们更好地理解范畴论。
对于人类认识世界,最神奇的一点就是这个世界居然是可以认识的,我们可以用自然语言描述它、我们可以用数学公式表示它,当然我们也可以用二维的图画描摹它,我们也可以把它看成三维的空间加一维的时间,也可以将三维空间和时间看成一体的,从而我们的世界是四维时空。
特指对象
现在我们做一个思想实验,在这个实验中,人类突然失去了语言能力,我们看到苹果,我们就本能地吃它,我们看到狮子,就本能地逃避,但是我们说不出,也认识不到苹果和狮子这两个符号。其实,我们的很多行为,都是这样的情况。比如,骑自行车,你需要练习和掌握,形成直觉和习惯,于是你就会骑自行车了,但是你可能对自行车运动的物理公式一无所知。同样,我们跑步、打篮球、游泳,也是一样,当我们做着这些行为时,我们并不是抽象思考和运算,而是依赖本能的直觉和习惯,并不依赖于语言。
现在,你要将这些直觉和习惯传递给另一个个体,怎么办呢?因为没有语言能力,其实没有什么特别好的办法,比如你想让同伴也会骑自行车,你只能不断骑,希望同伴能领会和模仿,但是同伴可能并不能会意,即使看到多次,也完全没有领会你是想让他学骑自行车。我们可以看到,个体间交流信息,必须有一个符号系统,这个符号系统双方要都能领会才行,在本能和直觉的世界,你的直觉驱使你向同伴展示骑车,而同伴的本能告诉他,你在骑车,没有别的意思,那么,你的意图就没法有效传递。
现在,让我们回到有语言的世界,我们突然发现,语言是如此重要,它是人与人沟通的桥梁和工具,而这个工具的核心是符号。比如,我们把经验中头顶最亮的部分叫做天,我们把脚踩的部分叫做地,我们把挡在前面的需要爬的土堆叫做山,把一种长者白色斑点有角的小型食草动物叫做梅花鹿,等等。于是,我们可以非常方便地描述世界,也能够愉快地和同伴交流了。
符号又是什么呢?符号就是事物的名字。我们反复观察到一个现象,给它取个名字,这就是符号。那取个名字是个什么意思呢?取个名字,就是一种映射,或者叫做对应,英文称为Mapping。比如,我说苹果这个名字,你想到了什么:
苹果 → 圆形的、红黄色的、甜的、带皮的、有果肉的….
在上述对应中:
-
苹果是符号,如果没有右半部分的对应物,这个符号没有任何意义
-
圆形的、红黄色的、甜的、带皮的、有果肉的….,这个右半部分,是符号的对应物,它的内涵很丰富,我们右半部分只写了一部分,他的全部内涵,一本书都写不完,如果我们需要把对苹果的描述精确到DNA特征,或分子级别的话
-
对应是一种抽象:当我们给右半部分取一个名字时,我们浓缩或者说忽略了苹果的具体内涵,把它所有的内涵作为一个整体,以苹果这个名字代之
我们在日常生活中,因为有语境的关系,所以我们对苹果的具体含义不会造成混肴。具体说,自然语言的苹果有三个含义,泛指含义、小泛指含义和特指含义。
我们先看泛指含义,如果我们把苹果这个名字所指代的所有东西,都放到一起,那么就是世界上所有的苹果,把它们一个个地放到一起,比如放到一个很大很大的箩筐里,这个箩筐,就构成了苹果集合,苹果集合这个大箩筐,里面是世界上所有的苹果。
我们在日常生活中也使用小泛指含义,以下是一些例子:
-
我想去买点苹果:大多数情况,指的是买某个数量/重量的一些苹果
-
这些苹果要做成苹果派:指的是眼面前的多个苹果
最后让我们看看特指含义:
-
把桌上的苹果递给我吃:指桌上的放着的一个具体苹果
-
这是我吃到的最甜的苹果:指一个在我看来最甜的苹果
-
我要吃一个苹果:指某个我未来要吃的苹果
因此,泛指含义指所有的,小泛指含义指在某个范围内的所有,特指含义指某个具体的。如果把泛指看成一个集合,那么小泛指就是泛指集合的某个子集,而特指则是泛指或小泛指中的一个具体元素。对于所有特指的东西,我们给它取个名字,叫做特指对象:
特指对象
名字对应的某个东西
下面我们取一个特指对象:苹果1,对于 苹果1 这个特指对象, 因为它是某个,因此我们可以用一个点表示它,于是我们有:

Figure 1. 特指对象
在上图中,点和苹果1,都代表同一个特指对象。用点表示这个特指对象非常形象,它有下面三层含义:
-
我们把特指对象画成一个点,表示它可以与世界的其他部分区分开来,即可以与其他的点(其他特指对象)和空白(世界中未取名字的部分)区分开来
-
特指对象不同于元素,一个集合的元素之间彼此独立,我们不考虑元素间的关系,特指对象之间可以考虑关系
-
如果名字不同,或者点不同,我们默认它们是不同的特指对象,除非特别说明多个名字或多个点是同一个特指对象的不同标记。
请看下图:
Figure 2. 不同的特指对象
在上图中,苹果1和苹果2是两个不同的特指对象,也就是说,是两个不同的苹果,除非在图中我们特别指明苹果1和苹果2是同一个苹果。
现在我们从上图反推特指对象,苹果1是一个名字,苹果2是一个名字,两个名字不同,我们没有特别说明苹果1和苹果2指同一个特指对象。因此就默认了这两个名字所代表的特指对象是可区分的(distinguishable),也就是说,是不同的。这两个特指对象哪里不同呢?也许大小不同、也许颜色不同,也许位置不同….,总之,苹果1指代的特指对象,和苹果2指代的特指对象,必然有某种属性,或者特征,使得我们可以断定,苹果1和苹果2不同。
特指对象间的关系
下面我们看看特指对象之间的关系,我们还是以苹果为例。止不住好奇心,我们观察了一下两个苹果的大小,发现苹果2比苹果1小,为了表示两个特指对象的这种关系,我们引入箭头,箭头的名字叫做“小于”,于是有:
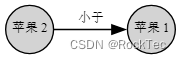
上面这个由点、箭头以及点和箭头的标记(名字)构成的图,叫做有向图。它是一种很有力的思维整理工具。这里的箭头有如下特征:
-
箭头的首尾必须分别连接一个特指对象
-
箭头将起点的对象映射(Mappping)到终点的对象,因此如果我们有一个箭头,那么就意味着必然有一个起点特指对象和一个终点特指对象
-
你可以将起点特指对象看作输入,经过箭头的mapping,我们得到了终点特指对象
有向图
下面我们做下推广,把你当下想到的特指对象,放到一起,看看它们是什么关系。这是笔者得到的一幅图:
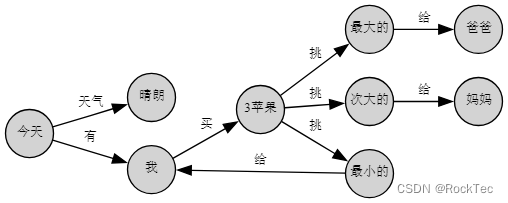
Figure 3. 分苹果有向图
这副图的含义是今天天气晴朗,我买了3个苹果,最大的给了爸爸,次大的给了妈妈,最小的给了我自己。可以看到,有向图可以较好地描述自然语言背后的结构,因此它是一种很好的整理思路的工具。在上图中:
-
上图中的点,全部是特指对象
-
3苹果是我买的三个苹果,一个整体,对应最大的一个、次大一个的和最小的一个苹果
-
今天对应晴朗,今天的晴朗
-
今天对应一个我,今天的我
-
每个箭头都取了一个名字
-
一个特指对象可以作为0条,1条,乃至于多条,甚至无限多条箭头的起点或终点
-
连续的起点和终点以及它们之间的箭头,可以形成环路
有向图与MindMap
我们再看一个有向图的例子:
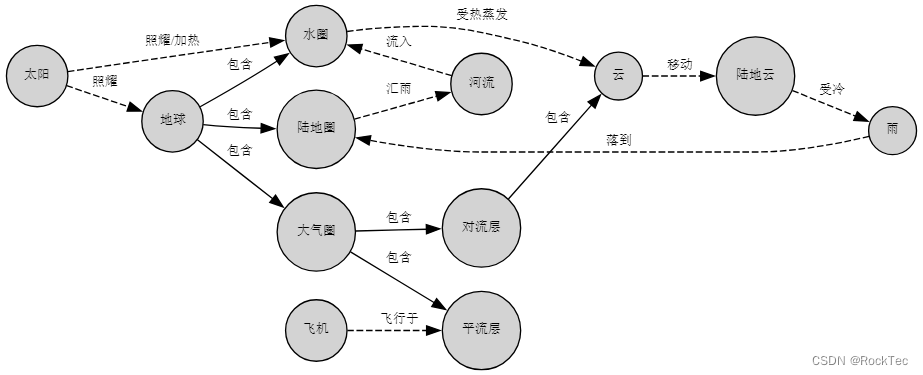
Figure 4. 地球圈
请看上图的实线部分,地球包含了水圈、陆地圈和大气圈,大气圈包含了对流层和平流层,对流层里包含云。这些箭头构成了一个树型结构,因此树型结构是有向图的一种特殊形式,而我们常用的思维导图(MindMap)也是树型结构,因此MindMap是有向图的一种特殊形式。
有向图形成的网状结构,可以从多个方面反映一个系统的结构,在上图中,我们还可以看到水圈的水受太阳照耀,受热会蒸发形成某朵云,这朵云飘到陆地,受冷降雨落到了地面,在地面上汇入河流,最后河流里的水再次回归大海。因此,对于一个系统结构的全面描述,有向图要有力得多,而思维导图(MindMap)对于包含关系描述或分类描述,则是很好的分析工具。
特指对象下的有向图
如果仔细考虑分苹果有向图和地球圈有向图,您可能会有些疑问:
对于分苹果有向图,3个苹果不一定有一个最大,一个中等大,一个最小,所以挑苹果的三个箭头不一定能成立。请注意,我们这里的3个苹果是特指对象,它是特定的三个苹果,具体地说,就是我在天气晴朗的今天买的3个苹果,它们恰好一个最大,一个中等大,一个最小。
对于地球圈有向图,升起的云不一定移动到陆地,变成陆地云,因此移动箭头不一定成立。请注意,我们这里的云是特指对象,这朵云恰好就移动到了陆地。如果我们要考虑云直接在海面上受冷变成雨的情况,我们就需要再举一个特指云对象:
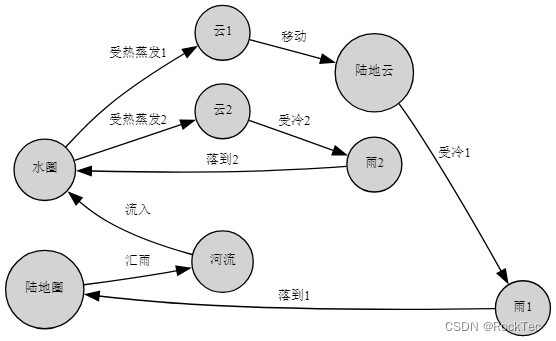
Figure 5. 多个特指云对象
如上图所示,我们有了云1和云2两个特指对象,分别表示两个特指云对象,一个飘向陆地,一个留在海面上。相应地,也有雨1和雨2,表示两个特指雨对象,一个落到大地上,一个落到海面上。
试想一下,如果要描述的系统有很多对象,那么我们就会有很多、很多相似的特指对象和箭头,例如上图中的云1、云2,和受热蒸发1,受热蒸发2等。一个更极端的例子是非负整数加操作,它的特指对象有无限多个,为简化起见,我们限定特指对象只有0,1,2,3,4:
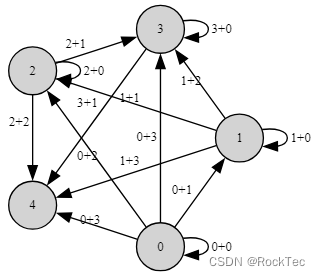
Figure 6. 整数1到4的加操作
如果把上图扩展到所有非负整数,那么具体对象就会有无穷多个,而每一个具体对象,都有无穷多条箭头指向大于或等于它的其他非负整数,因此我们说非负整数加操作富含特指对象和箭头。
在上图中,我们还注意到,从一个特指对象出发,经过箭头,可以回到该特指对象,也就是说,特指对象可以自指。
此外,特指对象有向图表达方式比较“原始”。从上图中我们可以看到,它巨细无遗地显示了非负整数加法的结构,以至于我们无法把所有非负整数加法的特指对象有向图完整画出来。但是,相应地,这种原始性,也意味着这种表达方式的基本性。按照前述特指对象的定义,它是一个有名字的某个东西,所有特指对象的共同特征就只有两个:有一个名字,可以作为箭头的起点或终点。因为一个名字可以指代任意的某个东西,因此它可以被应用到几乎任何语境,从而箭头也可以应用到任何语境,从而得到一个有向图。而名字到底指的什么,箭头到底什么意思,则取决于该语境。
有向图与准范畴
我们用特指对象画出的有向图并不是范畴论中所说的范畴,它是范畴论中范畴的一种弱化形式,我们给它取个名字:准范畴。
准范畴
由特指对象和箭头构成的结构
一个准范畴里有若干东西,每个东西有个名字,东西之间可以用箭头连起来,箭头也有个名字,可以画成一个有向图,如此而已,仅此而已。
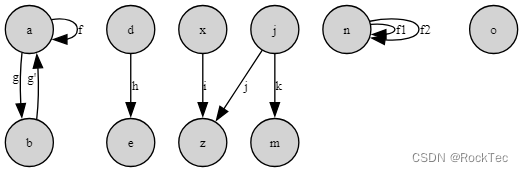
Figure 7. 准范畴示例
上图是一个准范畴的示例,点可以用箭头相连,也可以不相连。抽象地看这个图,也就是不考虑特指对象的具体语境:
-
我们不知道这些特指对象到底是什么,只知道它们是一些东西,并有个名字
-
我们不知道这些箭头到底是什么,只知道它们将一个特指对象对应到了另一个特指对象,并有个名字
通过准范畴,我们距离范畴的定义,就更近了一步。
这篇关于通俗范畴论2 有向图与准范畴的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





