有向图的负权值边与建模

本文主要是介绍有向图的负权值边与建模，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参见 dijkstra 算法为什么高效

昨天的文字最后提到 “经理办公桌上有一堆报表，让工人拟合一份最佳收支方案，工人用图论建模，就要使用 floyd，bellman-ford 算法。”，为什么工人的建模的熵减过程会出现负权重边，而自然的熵增过程不会出现负权重边，本文解释一二。

自然的过程如爆炸，河水泛滥，昆虫无意识漫游等，这些都遵循第一性原理，而人为的过程比如金融投资，成本估算，道路交通网络行为分析等，都需要注入能量，它们不是自然的过程，背后的原理不再是最小作用量，分析求解的方式自然不同。

以跑步为例来建模。

跑步需要付出成本，但它也能获得收益，将收益看作负成本，最终我们追求目标的就是 “一段周期内的跑步总成本最小”，以此来安排跑步计划，跑 x 休 y：
在这里插入图片描述

设跑步一天的成本为 a，收益是 b，而收益每天衰减系数为 c，跑 x 休 y 的总成本就是：

$A=a*x-b*x-\dfrac{b*c(1-c^y)}{1-c}$

基于此，我们可以规划一个比较久的跑步时间，比如一年，然后在这一年中按固定跑 1 休 0，或跑 1 休 1，或跑 3 休 1，或跑 5 休 2，或在一长段时间随机 x，y，调节参数 a，b，c。

将每个计划的每一个跑休周期看做一条边，该周期的总成本 A 视为该边权重(它可能为负数)，每个计划的起点视作顶点，跑步开始时间视作源顶点 S，结束时间视作目标顶点 D，事情就变成了求 S 到 D 的最短路径问题：
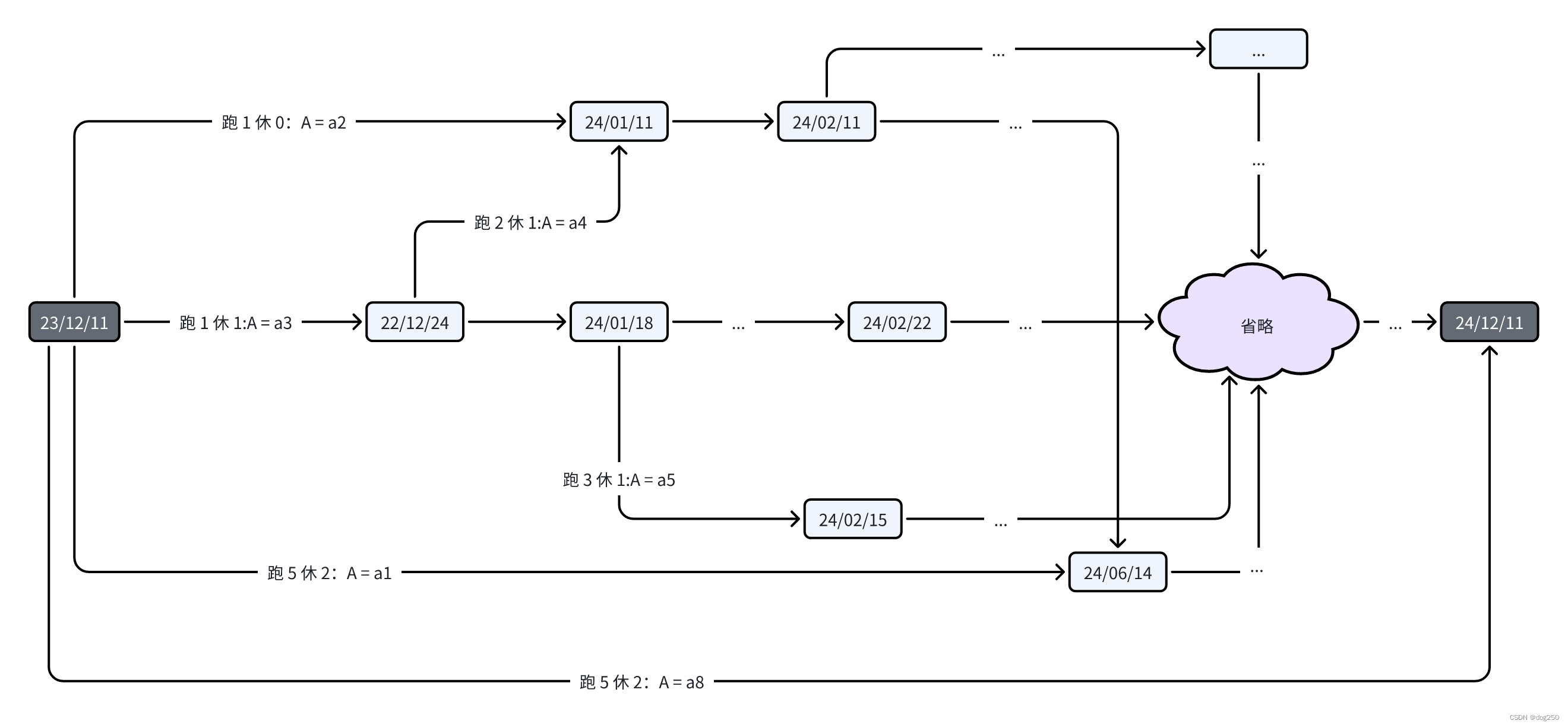
在这里插入图片描述

找到的最短路径就是最佳的跑步计划。类似的还可以用这个模型规划读书计划，生意买卖等和收支有关的计划，其中的关键在于边权重可以是负数。

负数权重显然是一种附着 “人为解释” 的权重，而不是 “自然的距离”，比如路由器之间链路的长度，传输 delay 都是自然距离，但如果规定何时走某条路有收取拥塞税进而增加 cost 度量，或奖励突发令牌，则属于人为附加权重了。

图论算法中，自然的最短距离，比如求物理最短距离或可划归为物理最短距离，那非 dijkstra 算法莫属，但人为建模的应用题，则要考虑边的负数权重，这种情况下必须通过遍历松弛来求解，而不能使用 “利用自然熵增” 的算法，因为假设不再成立了。至于单源还是多源最短路径，属于问题空间之外的话题，与本文讨论关系不大。