poj 3259： 题意：John的农场里n块地，m条路连接两块地，w个虫洞，虫洞是一条单向路，不但会把你传送到目的地，而且时间会倒退Ts。 任务是求你会不会在从某块地出发后又回来，看到了离开之前的自己。 判断树中是否存在负权回路就ok了。 bellman代码： #include<stdio.h>const int MaxN = 501;//农场数const int

题目：Bellman_ford:优化算法 题目链接： 94. 城市间货物运输 I (kamacoder.com) 代码： #include<bits/stdc++.h>using namespace std;struct Edge {int to;int val;Edge(int t, int w) :to(t), val(w) {}};int main() {int n, m;c

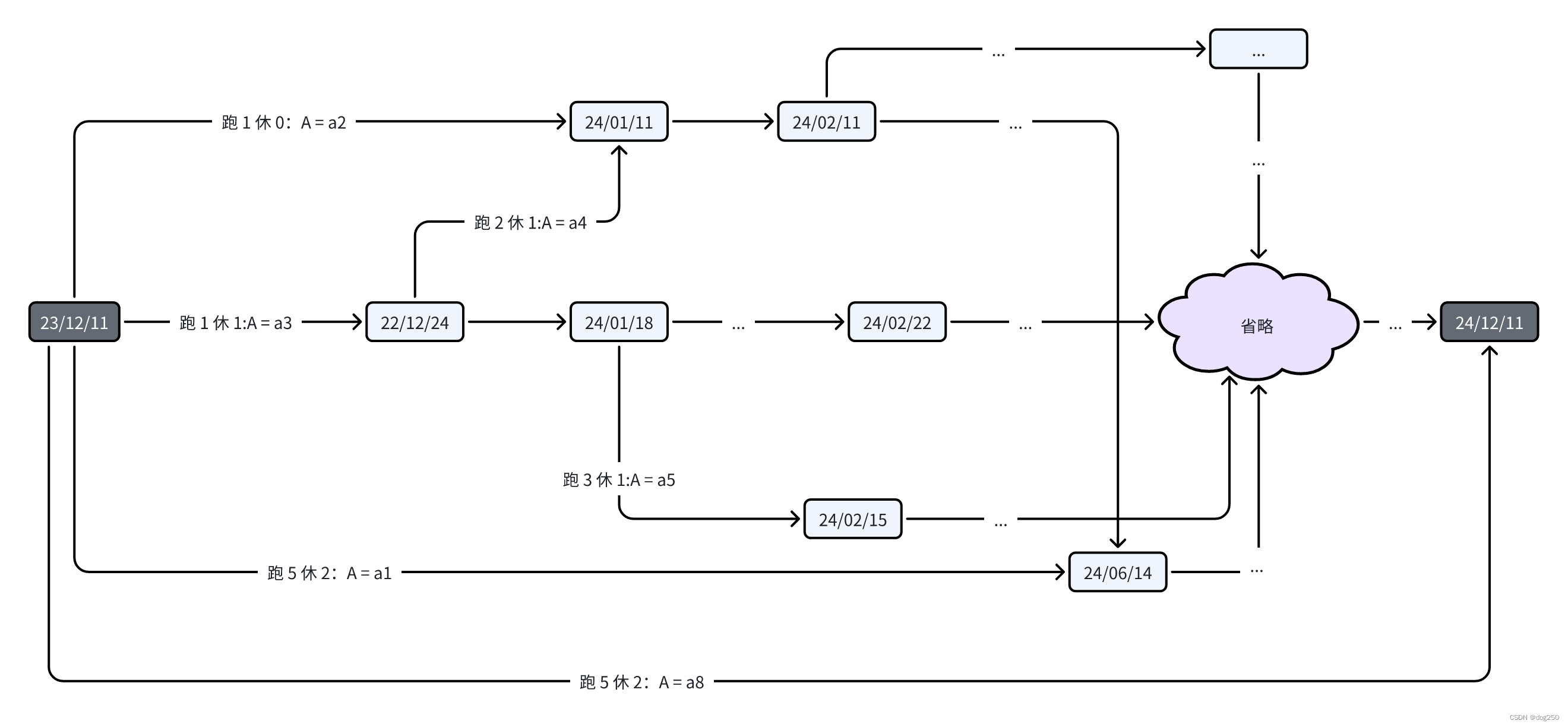
参见 dijkstra 算法为什么高效 昨天的文字最后提到 “经理办公桌上有一堆报表，让工人拟合一份最佳收支方案，工人用图论建模，就要使用 floyd，bellman-ford 算法。”，为什么工人的建模的熵减过程会出现负权重边，而自然的熵增过程不会出现负权重边，本文解释一二。 自然的过程如爆炸，河水泛滥，昆虫无意识漫游等，这些都遵循第一性原理，而人为的过程比如金融投资，成本估算，道路交通网络

1.负权边回路首先dist数组刚开始初始化是0，（因为是检测回路，那么无论从哪里开始起点都是一样的，所以一开始就会把所有点都加载到队列中，所以就相当于把dist[所有点] = 0）；下面就是cnt数组----很多人应该都看过模板长什么样子了，其中的cnt为什么要大于n才算有回路？其实是如果存在负权回路，那么这条路肯定是一直减少的，所以当走过的路大于n条，还是<0，那一定是存在负权回路的！

题目描述 输入一个有向网络图，边的权值可正可负，求顶点1到其他各点的最短路。题中数据保证无负权环。 输入描述 输入文件第一行为 n 和 m（ n,m≤20），表示 n 个顶点和 m 条边，接下来有 m 行，每行三个整数 i、j、k，代表从顶点 i 到顶点 j有一条边，且权值为 k（ −100≤k≤100）。 输出描述 输出文件为一行，有 n−1个数据，即顶点1到其他各顶点间的最短路径长度

本文参考了书目《算法笔记》     对于一个图如果存在零环、正环，利用Bellman-Ford算法不会影响到最短路径的求解；如果一个图出现了负环，则会导致恶性循环，会导致dis[u]出现负无穷，永远也求解不出来，但如果从源点出发，无法到达负环，则最短路径的求解不会收到影响（不在负环上的dis[u]可以求出确切值，在负环上的点v，标记dis[v]为不可达就行了）   下面是代码： #in

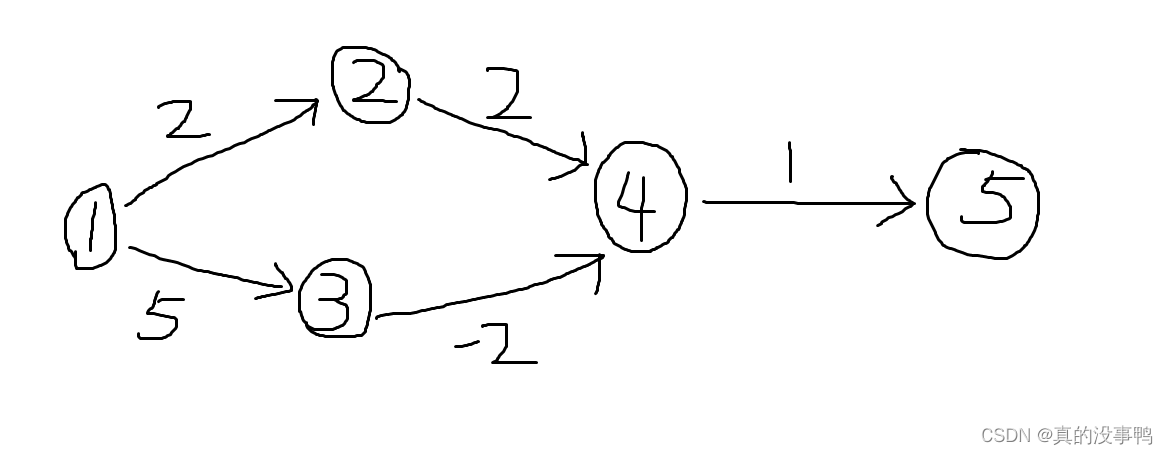
之前我们说了Dijkstra算法不能解决带有负权边的图，这是为什么呢？下面用一个例子讲解一下 以这里图为例，一共有五个点，也就说要循环5次，确定每个点的最短距离 用dijkstra算法解决的的详细步骤 1，初始dist[1] = 0，1号点距离起点1的距离为0 2，找到了未标识且离起点1最近的结点1，标记1号点，用1号点更新和它相连点的距离，2号点被更新成dist[2] = 2，3号点

之前我们说了Dijkstra算法不能解决带有负权边的图，这是为什么呢？下面用一个例子讲解一下 以这里图为例，一共有五个点，也就说要循环5次，确定每个点的最短距离 用dijkstra算法解决的的详细步骤 1，初始dist[1] = 0，1号点距离起点1的距离为0 2，找到了未标识且离起点1最近的结点1，标记1号点，用1号点更新和它相连点的距离，2号点被更新成dist[2] = 2，3号点