本文主要是介绍【Eviews实战】——ARIMA模型建模,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 数据背景
- 2 时序可视化
- 3 平稳性检验
- 4 一阶差分后序列
- 5 模型定阶
- 6 模型估计
- 7 模型改进
- 8 模型拟合
- 9 模型预测
目的:熟悉eviews基本操作, 通过建立ARIMA模型进行时间序列预测。
该篇文章对1990年1月-1997年12月我国消费价格指数进行平稳性检验,并利用ARIMA模型预测未来6个月消费价格指数变动情况。文章涉及ADF检验; τ \tau τ检验;t检验、自回归过程、移动平均过程等。
1 数据背景
我国1990年1月-1997年12月消费价格指数数据,数据来源于实验课数据文件,部分数据如表1所示。
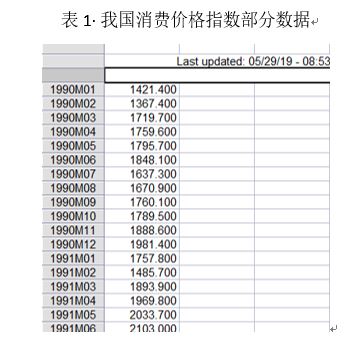
2 时序可视化
利用eviews10.0绘制1990年1月-1997年12月我国消费价格指数数据时序图:
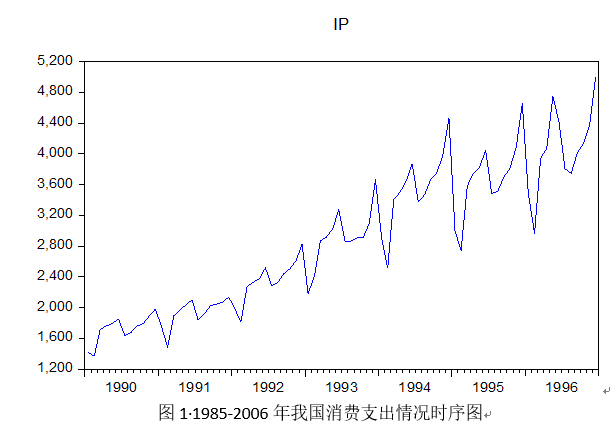
由图1可以看出,我国消费价格指数数据存在趋势项和截距项,为非平稳数据,接下来利用ADF单位根检验并判断其所属类型。
3 平稳性检验
首先检验原序列的平稳性,根据ADF检验模型:
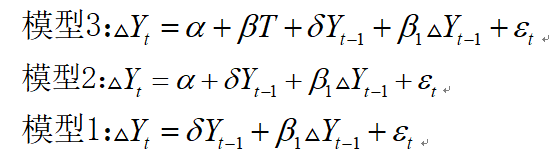
利用eviews10.0分别对三个模型进行ADF检验得到结果:
①模型3:
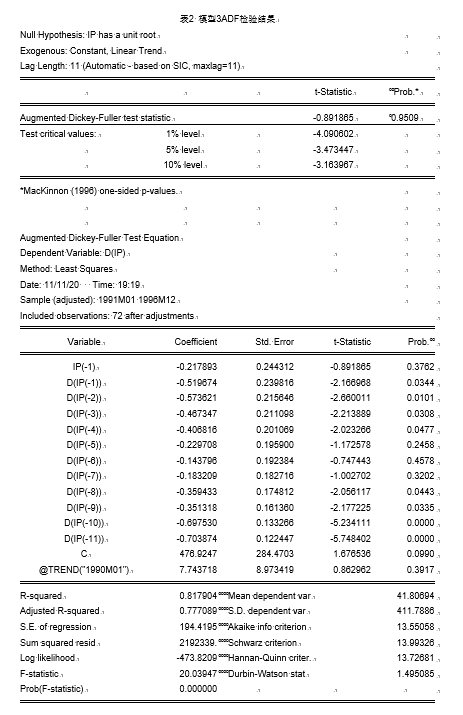
结果显示, τ \tau τ统计量显示结果不拒绝显著性水平为0.05的原假设,继续模型2的单位根检验。
②模型2:
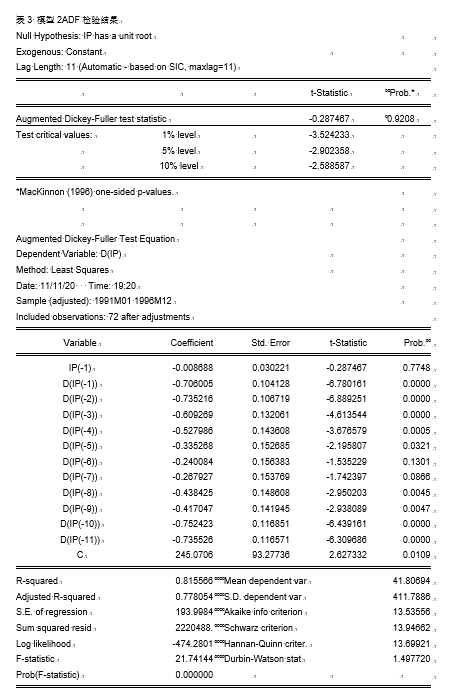
结果显示, τ \tau τ统计量显示结果不拒绝显著性水平为0.05的原假设,继续模型1的单位根检验。
③模型1:
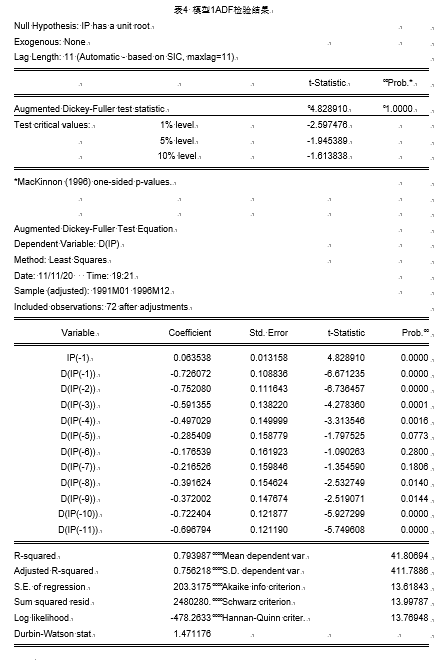
结果显示, τ \tau τ统计量显示结果不拒绝显著性水平为0.05的原假设,三种模型检验均未通过显著性检验,说明原序列是非平稳序列,且三种情形下,检验模型对应的AIC、SC、HQ值如表5所示。
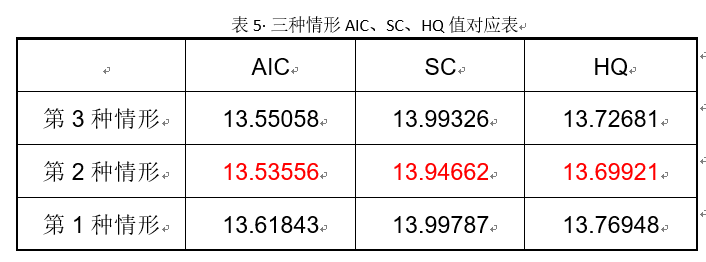
由5单位根检验可知,综合三种情况下的AIC、SC、HQ信息准则的值可知,第2种情形的值最小,即该序列为存在截距项的单位根过程。继续检验其一阶差分后的序列是否平稳。
4 一阶差分后序列
根据ADF检验模型:
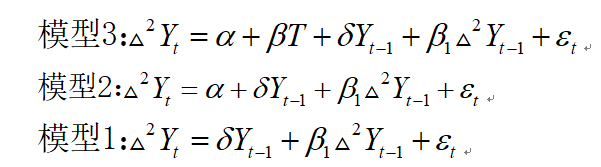
其中, △ 2 Y t \bigtriangleup ^2Y_t △2Yt表示对 Y t Y_t Yt进行两次差分。
利用eviews10.0分别对三个模型进行ADF检验得到结果:
①模型3:
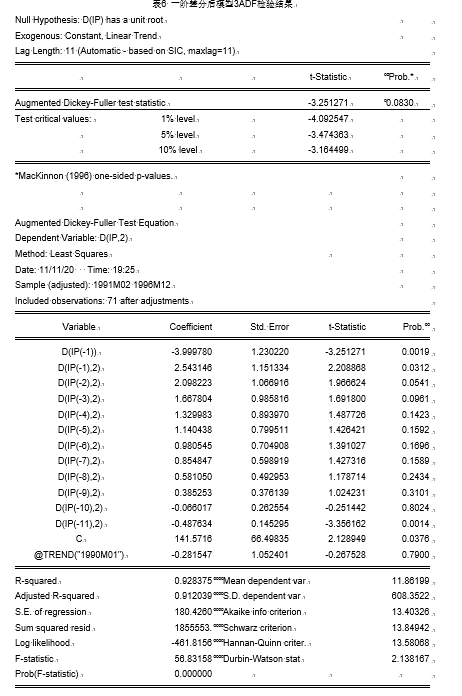
结果显示, τ \tau τ统计量显示结果拒绝显著性水平为0.05的原假设,同时,趋势项@TREND(“1985”)通过显著性水平为0.05的显著性检验,可得到我国人均食品消费支出的1阶差分序列是平稳的,但截距项未通过显著性水平为0.05的显著性检验,为使结果比较更为细致,继续进行模型2、模型1的单位根检验。
②模型2:
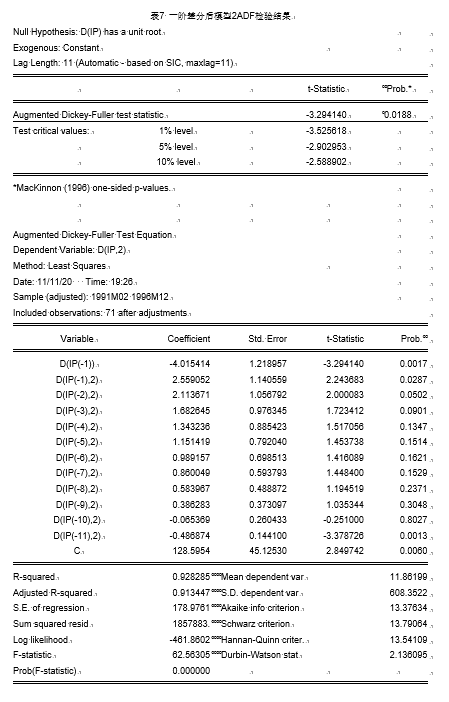
结果显示, τ \tau τ统计量显示结果拒绝显著性水平为0.05的原假设,同时,截距项通过显著性水平为0.05的显著性检验,表明即该序列ip(我国消费价格指数)的一阶差分序列是平稳序列,即一阶单整,计为I(1),说明经过一阶差分后,实验数据符合ARIMA模型的平稳性条件。
5 模型定阶
通过图2和表8可初步判定建立ARIMA(2,1,2)模型。
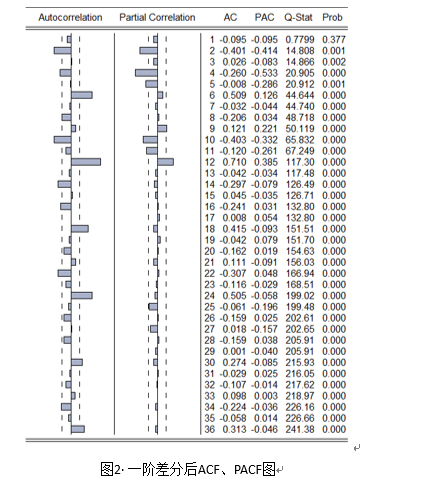
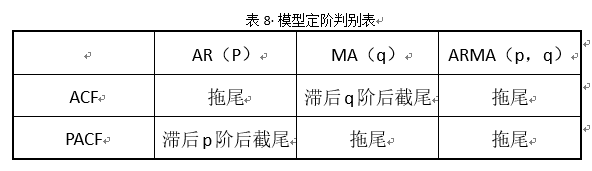
通过图2和表8可初步判定建立ARIMA(2,1,2)模型。

6 模型估计
利用eviews10.0得到回归结果:
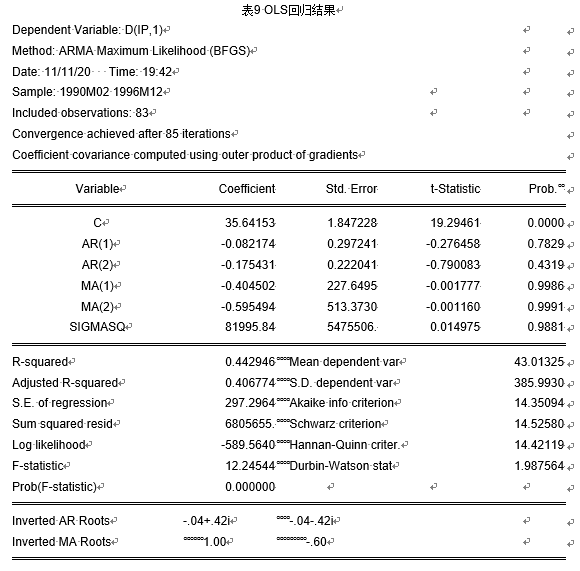
回归结果显示,拟合效果并不是很好,且存在移动平均单位根为1,模型并不稳定,故通过改进AR(p),MA(q)进行改进。
7 模型改进
通过改进一阶差分后消费价格指数与自回归、移动平均组合方式寻找最优模型。
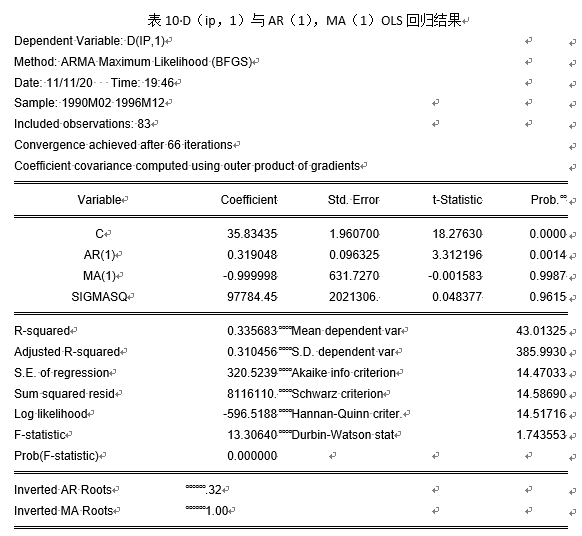
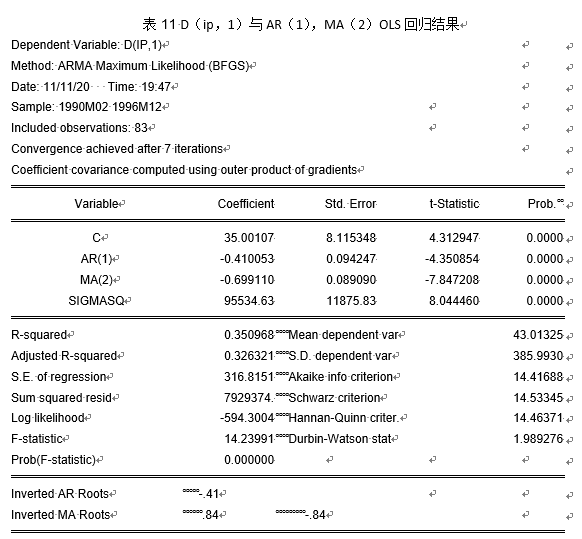
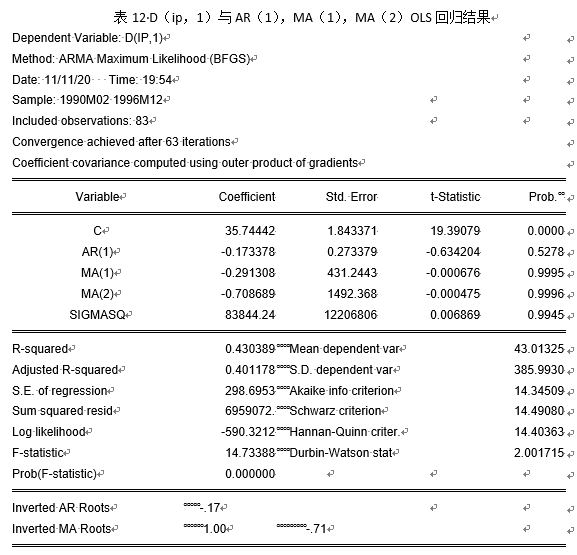
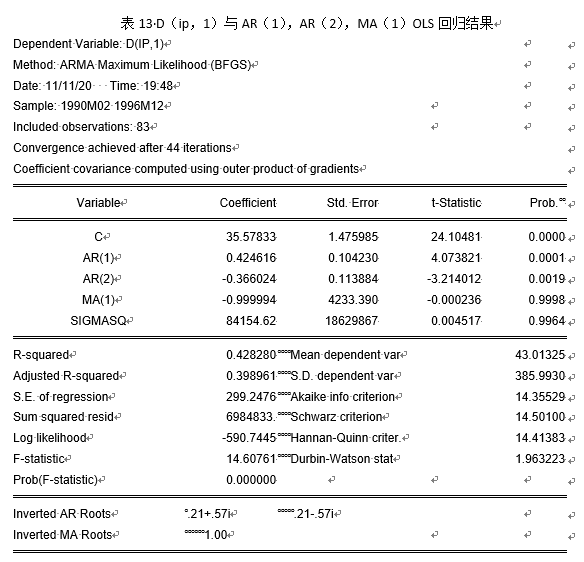
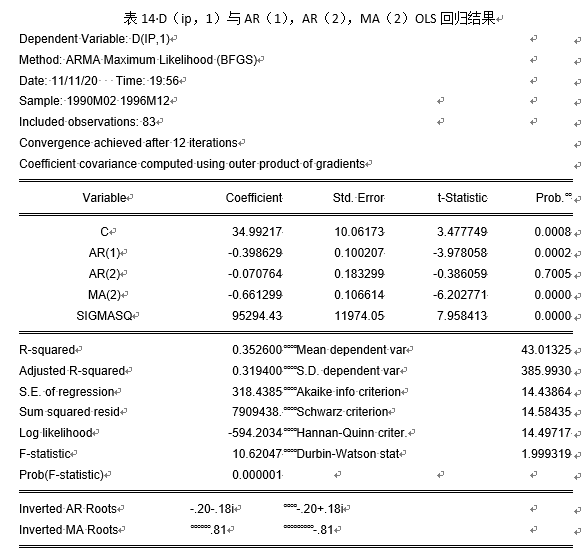

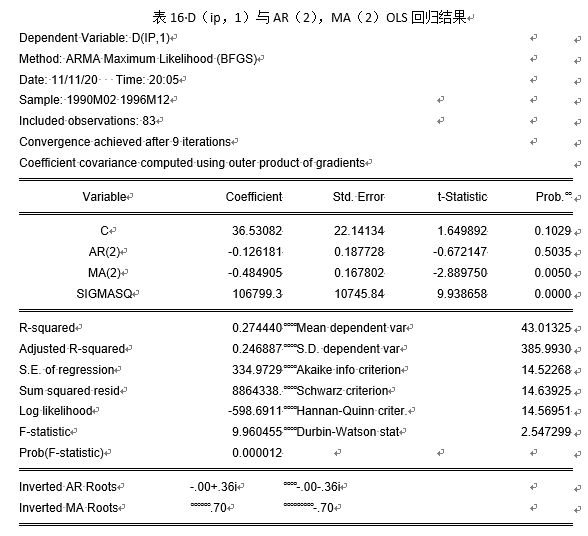
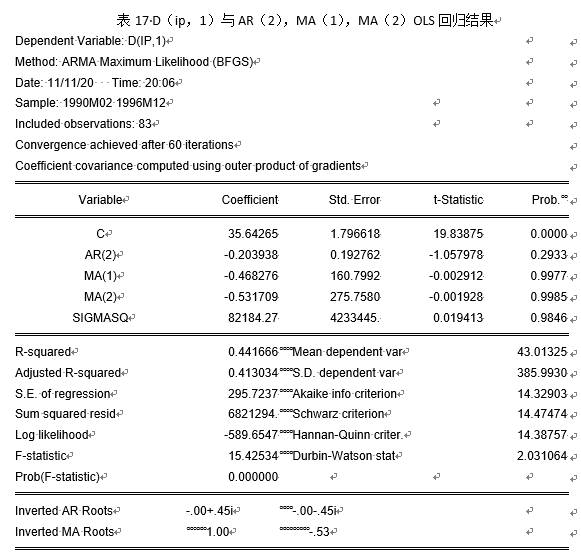
模型改进后结果汇总见表18。
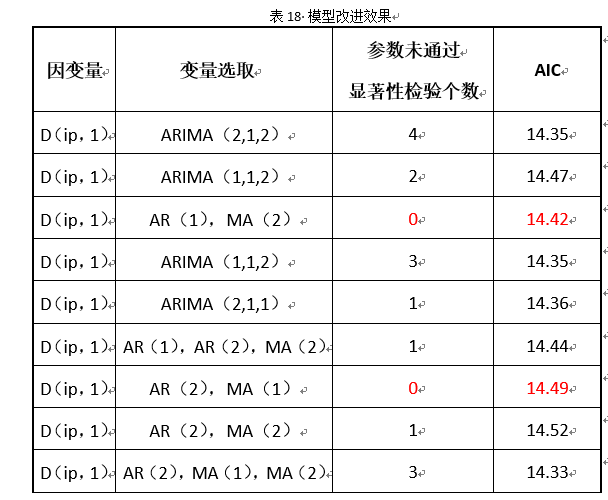
通过图18显示,自变量选取AR(1),MA(2)时参数均通过0.05显著性水平的显著性检验,且AIC相对于变量选取AR(2),MA(1)更小,同时,AR与MA单位根如图3所示:
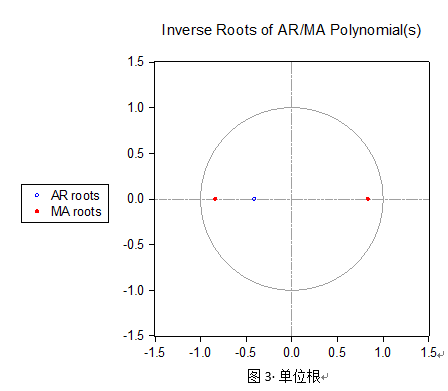
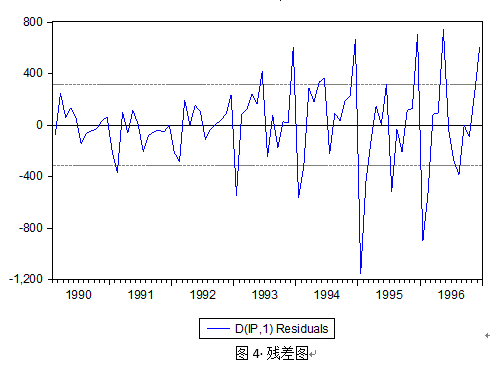
由图3显示,AR、MA单位根均小于1,模型估计具有稳定性,同时根据残差图及残差ACF、PACF可以判断回归方程残差序列趋于平稳,为白噪声序列,模型建立成功。

故选取最终模型:

8 模型拟合

由图5可以看出,回归方程的拟合效果较好。
9 模型预测
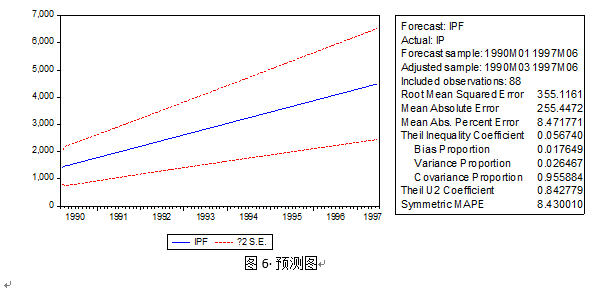
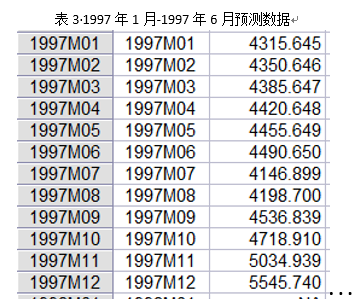
根据图6和表3,看可以看出,未来一段时间居民消费价格指数总体呈上升趋势。
这篇关于【Eviews实战】——ARIMA模型建模的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







