【博士每天一篇文献-综述】Brain network communication_ concepts, models and applications

本文主要是介绍【博士每天一篇文献-综述】Brain network communication_ concepts, models and applications，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阅读时间：2023-12-1

1 介绍

年份：2023
作者：Caio Seguin，Olaf Sporns印第安纳大学心理与脑科学系
期刊： nature reviews neuroscience
引用量：33
中文翻译参考：https://swarma.org/?p=44524

本文主要讨论了脑网络通信的概念、模型和应用。脑网络通信模型可分为三大类：扩散过程、参数模型和路由协议。每个系列又分为多种通信模型，每种模型都提出特定的策略或算法来引导网络节点之间的信号传递。根据通信成本的三个维度：延迟、信息和能量，可以从概念上评估一个模式的优缺点。对每种模型给出了多个详细的量化指标。此外，本文通过一些例子展示了脑网络通信模型如何为研究健康和疾病中的大脑功能提供一个多功能、可相互解释和可计算的框架。

2 创新点

（1）结合了图论和网络科学概念来描述和量化大脑结构连接组中信息传递的模型。
（2）将网络通信模型和测量方法根据信号概念进行归纳，并对其生物学合理性进行定性评估。
（3）探讨了这些模型在基础、认知和临床脑科学等关键领域中的新兴应用，展示了网络通信作为研究大脑功能的多功能框架。
（4）提出了未来指导网络通信模型开发、应用和验证的建议。
（5）利用大量直接电刺激数据集研究人脑中的经验信号传输，并绘制了全脑因果关系刺激传播图，以探索神经信号传输的特点。
（6）发现通信测量能够准确预测通过白质连通性发出的信号，对不同预测因子的解释力进行比较，发现搜索信息和可交流性优于其他交流测量指标。

3 关键知识点

（1）脑网络通信模型概念
脑网络通信模型描述了通过连接组传递信号的策略。人类连接组是由灰质区域（网络节点）与白质束（网络连边）相互连接而成的宏观连接网络。
脑网络通信模型是通过结构连接引导信号传播的策略。该模型确定了从节点到节点之间的路径，通信测量方法量化该模型确定的路径的特征，包括效率（efficiency）、成本（cost）和弹性（resilience）。网络通信模型和度量可以在无向（双边连接）或有向（非对称连接）以及无权重（仅表示存在或不存在连接）或有权重（表示连接强度）的结构网络中计算。
（2）网络通信成本的三个维度：延迟（delay）、信息（information）和能量（energy）

• 延迟成本指信号传输的拓扑效率（或速度）
• 信息成本指引导信号传播所需的网络知识量
• 能量成本指信号传递所必须的代谢资源量

（3）最短路径概念
脑网络中节点之间通信的路径长度表示沿该路径传播信号的成本大小。最短路径最有效率。通过最大限度减少在两个节点间传递的步数，最短路径可以最大限度减少信号传输延迟以及穿过突触和沿轴突传播信号时的代谢消耗。但是要计算最短路径需要了解整个网络的拓扑结构。

（4）三种通信模型

• 扩散过程（diffusion processes）：信号沿着多个网络前端进行广播，或通过随机游走动力学传播。与路由协议不同的是，扩散过程不要求单个神经元掌握其周边以外的连接组知识，然而这种传播方式需要更多信号重传才能建立节点间的通信。因此，扩散模型具有较低的信息成本，高延迟和高能量成本的特点。
• 路由协议（Routing protocols）：信号是通过高效、选择性访问的少量路径传递的。信号在连接组中是沿单一、有选择的路径传输的。路由协议旨在找到由强大而可靠的少量连边组成的路径，从而高效、准确地传输信号。路由模型具有较高的信息成本、低延迟、低能量成本的特点。
• 参数模型（parametric models）结合了路由和扩散的要素，根据模型参数的调整，提出倾向于通过有效路径或随机游走进行通信的混合策略。

以上不同的通信模型的性能可通过一系列通信指标来量化，衡量标准根据其量化的神经通信特征（如信号成本或弹性）进行分组并用颜色编码。

• AT，激活时间
• Cinfo，信息成本
• CMY，可交流性
• Ctrans，传输成本（相当于 MFPT）
• DE，扩散效率
• EDP，边缘不连接路径
• ER，效率比
• k-SPL，k-最短路径长度
• MFPT，平均首次通过时间
• NE，导航效率
• NPL，导航路径长度
• PT，路径传递性
• RE，资源效率
• SI，搜索信息
• SPE，最短路径效率
• SPL，最短路径长度
• SR，成功率

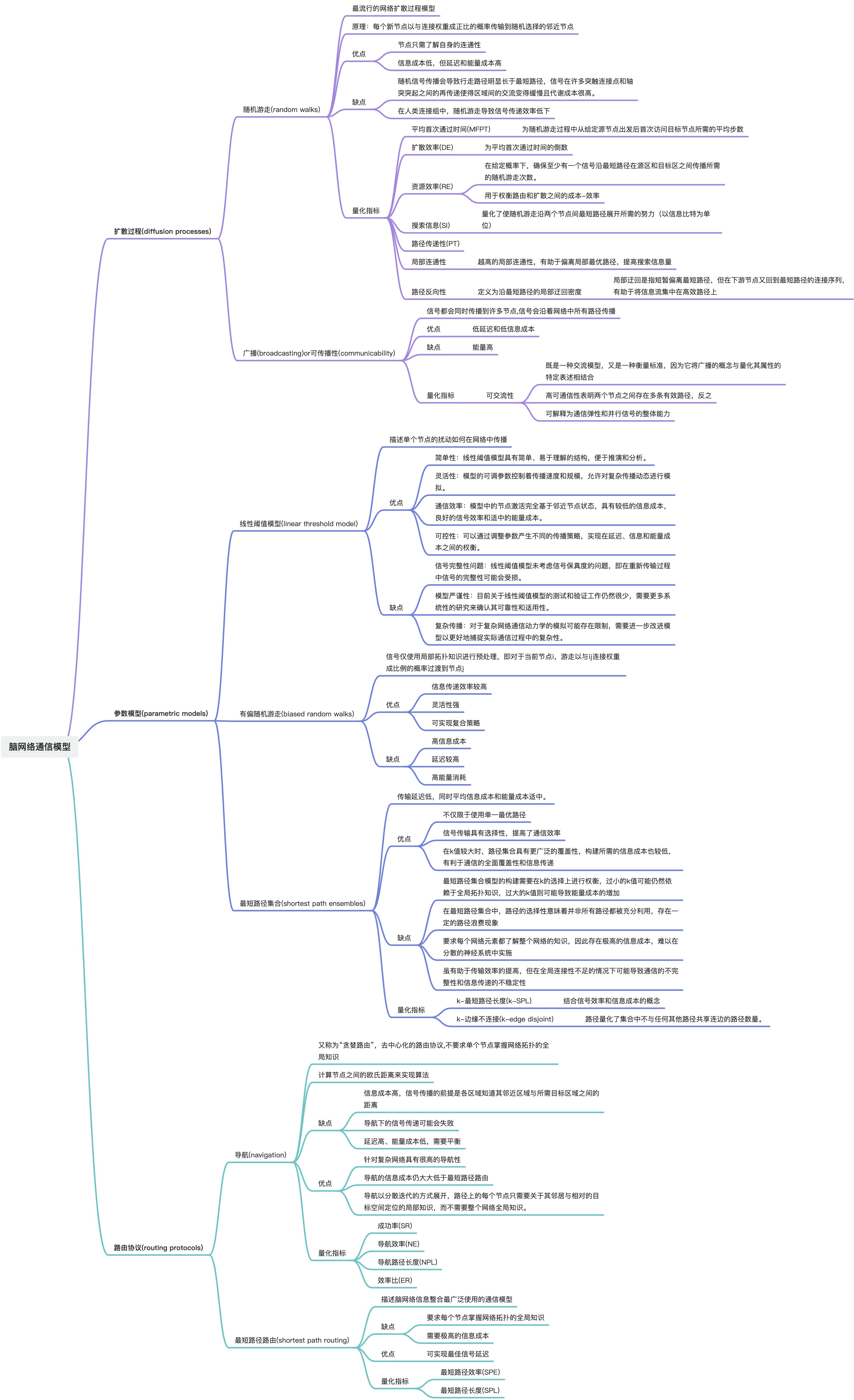
（5）路由协议模型算法原理

1. 最短路径路由是最常用的通信模型，它认为信号传递沿着连接两个区域的最有效路径进行。这意味着在选择通信路径时，会优先考虑最短的路径，以实现最佳信号延迟和节约能量消耗。最短路径路由的算法要求每个网络元素了解整个网络的拓扑结构，以找到最佳通信路径。这就意味着在确定最短路径时，需要有高信息成本的支持，因为每个节点都需要掌握整个网络的情况。
2. 导航是一种去中心化的路由协议通信模型，不需要单个节点了解整个网络的拓扑知识。导航通过基于节点距离的局部知识来确定通信路径，从源节点到目标节点的路由是通过每个节点将信号转发给距离目标最近的邻节点来实现的。导航的贪婪路由策略可能会导致信号传递失败或陷入循环，但复杂网络具有很高的导航性，即成功传播信号并找到有效路径的能力。因此，导航作为另一种路由协议提供了一种与最短路径路由不同的通信策略。

（6）扩散模型之可传播性的算法原理

1. 信号源开始向相邻区域发送信号，划定所有单位长度的路径，使信号传播到直接相连的区域。
2. 接收到信号的区域将信号传播给所有相邻区域，划分出从信号源开始所有长度为2的可能路径。
3. 所有可能的路径集合包括最短路径。
4. 在广播过程中，信号从首次离开信号源到首次到达目标区域的延迟与最短路径路由的延迟相同。
5. 路由过程遵循“细粒度、粗粒度、细粒度”的传播模式，即信号沿着较短路径传播，随着路径变长，低效路径的总体贡献会迅速减少；对节点间的可通信性进行加权和计算，以确保短路径比长路径更重要。
6. 可传播性模型是一种在大脑网络中广泛应用的特定广播模型，其中信号同时沿网络的多个路径传播。
7. 可传播性衡量了两个节点之间存在多少有效路径，体现了通信弹性和并行信号传播的整体能力。

（7）参数模型的算法原理
参数模型的行为由可调参数控制，可调参数沿一连续可能值定义。在这个范围两端，参数值通常近似于通过路由或扩散进行通信，而中间值则实现混合策略。对参数进行仔细调整后，就能产生复合策略，在延迟、信息和能量成本之间实现有利权衡，而这是路由和扩散，两种截然相反的策略，所无法实现的。
（8）参数模型之线性阈值模型的算法原理及优缺点
线性阈值模型是描述节点扰动在网络中传播的模型，算法步骤如下：

1. 模型假设：线性阈值模型假设网络中的每个节点在任何给定时间点处于“活跃”或“不活跃”状态，其中“活跃”状态表示节点已经接收并传播了扰动。
2. 阈值参数设置：模型的阈值参数!∈[0,1]控制着级联的速度和规模，该参数决定了节点何时会处于“活跃”状态。如果节点的邻居中有大于阈值参数比例的节点处于“活跃”状态，那么该节点将被激活。
3. 激活时间计算：激活时间是线性阈值模型的主要通信指标，用于量化网络中扰动传播时两个节点激活之间的延迟。
4. 级联传播：局部节点扰动会触发通信级联，沿着多个网络节点传播，由节点的局部知识决定激活的方式。节点状态的传播基于邻居节点的状态。
5. 参数调节：线性阈值模型中的可调参数可以调节参数值以产生不同模式的传播动力学，如延迟、信息和能量成本的权衡。
6. 有偏随机游走：有偏随机游走是对线性阈值模型的一种参数化表述，通过增加参数“来引导节点利用全局拓扑信息进行通信，最终收敛到最短路径路由。

优点

• 简单性：线性阈值模型具有简单、易于理解的结构，便于推演和分析。
• 灵活性：模型的可调参数控制着传播速度和规模，允许对复杂传播动态进行模拟。
• 通信效率：模型中的节点激活完全基于邻近节点状态，具有较低的信息成本，良好的信号效率和适中的能量成本。
• 可控性：可以通过调整参数产生不同的传播策略，实现在延迟、信息和能量成本之间的权衡。

缺点

• 信号完整性问题：线性阈值模型未考虑信号保真度的问题，即在重新传输过程中信号的完整性可能会受损。
• 模型严谨性：目前关于线性阈值模型的测试和验证工作仍然很少，需要更多系统性的研究来确认其可靠性和适用性。
• 复杂传播：对于复杂网络通信动力学的模拟可能存在限制，需要进一步改进模型以更好地捕捉实际通信过程中的复杂性。

（9）参数模型之有偏游走模型的算法原理及优缺点

1. 参数化表述：在有偏随机游走模型中，节点可利用的全局拓扑信息量由参数控制。
2. 偏差因素：有偏随机游走使用额外因素来影响过渡概率，这些因素可以代表网络元素的内在属性，如个体在社交网络中的地位。
3. 信号传输：信号从源节点出发，以与连接权重成正比的概率传输到随机选择的邻近节点，直到到达目标节点为止。这一过程被称为“无偏”随机游走。
4. 通信动力学：有偏随机游走模型的参数值影响通信成本和行走路径，从无偏随机游走到最短路径路由等通信策略的连续谱提供灵活的探索方式。
5. 路由模式：游走过程中可能出现“细粒度、粗粒度、细粒度”的传播模式，依赖于高聚类和互联枢纽核心的支持。
6. 资源效率评估：资源效率可通过测量路径加权和和资源效率来评估，以量化路由和扩散之间的成本-效率权衡。

信号传播方式：扩散过程是一种分散的神经通信概念，信号沿着多个网络前端进行广播，或通过随机游走动力学进行传播，不要求单个节点掌握周围连接。
优点

• 提高信息传递效率：有偏随机游走算法通过引入额外因素来影响过渡概率，使信号更有可能在通往所需目标的最短路径上传输，从而提高信息传递效率。
• 灵活性强：通过调整参数"的值，有偏随机游走算法可以灵活地在无偏随机游走和最短路径路由之间进行权衡，实现信息成本和延迟之间的平衡。
• 可实现复合策略：有偏随机游走算法通过调整参数值，可以实现既具有路由优势又具有扩散优势的复合策略，提高通信效率。
• 相对低能量成本：导航策略在信息成本适中的情况下，具有低延迟和低能量成本的优势，可能比最短路径路由更符合生物学实际。

缺点：

1. 高信息成本：有偏随机游走算法中，引入额外因素会增加信息传递的成本，使信息传播的前提是各区域知道其邻近区域与目标区域之间的距离，导致信息成本较高。
2. 延迟较高：由于有偏随机游走算法会使信号路径明显长于最短路径且信号在多个连接点和轴突间再传递，导致通信延迟较高。
3. 高能量消耗：通过增加信号副本来提高效率可能会导致更高的新陈代谢需求，即增加了能量消耗。

（10）最短路径集合（shortest path ensembles）的算法原理及优缺点

1. 确定节点间最有效的前k条路径：最短路径集合模型考虑信号在两个节点之间的传输通过连接它们的k条最有效路径组成的集合进行。这意味着需要确定节点对之间的前k条最有效路径，以支持通信并减少传输延迟和成本。
2. 考虑路径可达性和通信成本：随着k值的增大，路径集合变得更庞大且具有包容性，而确定的路径集合构建所需的信息成本也较低。同时，在选择最短路径时要考虑通信成本和延迟，以保证通信的高效率和节约资源。
3. 路由选择性特点：最短路径集合模型突显了通信的选择性，即通信只通过最短路径进行，从而减少新陈代谢消耗。
4. 考虑全局通信效率：最短路径集合模型下的信号传递需通过几种网络通信测量方法进行量化，以评估通信效率和网络属性。同时，需要考虑全局效率和分布式系统中的通信模式。

优点：

• 最短路径集合模型突显了信号在整个网络中传输时并不仅限于使用单一最优路径的理念。
• 通过考虑节点间的前k条最有效路径，最短路径集合模型允许信号传输具有选择性，提高了通信效率。
• 在k值较大时，路径集合具有更广泛的覆盖性，构建所需的信息成本也较低，有利于通信的全面覆盖性和信息传递。
• 最短路径集合模型在传输延迟低、平均信息成本和能量成本适中的情况下，为神经通信提供了一种有效的方式。

缺点：

• 最短路径集合模型的构建需要在k的选择上进行权衡，过小的k值可能仍然依赖于全局拓扑知识，过大的k值则可能导致能量成本的增加。
• 在最短路径集合中，路径的选择性意味着并非所有路径都被充分利用，存在一定的路径浪费现象。
• 传统最短路径路由模型中的缺点在于其要求每个网络元素都了解整个网络的知识，因此存在极高的信息成本，难以在分散的神经系统中实施。
• 最短路径集合模型虽有助于传输效率的提高，但在全局连接性不足的情况下可能导致通信的不完整性和信息传递的不稳定性。

（5）分析角度

• 计算连接矩阵

在连接组上计算网络通信度量可得到一个通信矩阵，该矩阵可量化网络通信模型下每对节点（解剖学上连接或未连接）之间信号传递的推定属性。矩阵将结构连通性的网络转化为神经元对间信号传递的定量估计。

4 实现工具箱

本文中的所有算法，都在Brain Connectivity Toolbox工具箱中，详细介绍https://sites.google.com/site/bctnet/
（1）bctpy：Python 的大脑连接工具箱。
（2）bct-cpp：C++ 中的大脑连接工具箱。
（3）人类连接组项目：NIH 联盟，用于绘制大脑白质通路。
（4）虚拟大脑项目：一个模拟灵长类大脑网络动力学的联盟。
（5）FieldTrip：MEG、EEG 和侵入性电生理数据的高级分析工具箱。
（6）CONN：用于计算、显示和分析 fcMRI 数据的跨平台软件。
（7）DSI-Studio：用于扩散 MRI 分析的纤维束成像软件工具箱。
（8）GraphVar：一个用户友好的基于 GUI 的工具箱，用于大脑连接的图形分析。
（9）基于网络的统计工具箱：用于测试有关连接组的假设的工具箱。
（10）WFU_MMNET：用于脑网络多元建模的工具箱
（11）神经影像分析套件：用于 fMRI 处理的模块和管道库。
（12）图论 GLM 工具箱：脑网络图分析属性的 GLM 工具箱。
（13）Brainnetome Toolkit：复杂网络测量的 MATLAB GUI 工具包。
（14）BioNeCT：一个用于分析脑电图记录中的大脑网络连接性的有凝聚力的平台。
（15）GRETNA：用于全面分析大脑连接组拓扑的工具箱。
（16）MIBCA：具有批处理功能的自动化一体式连接工具箱。
（17）GAT/bnets：功能和结构大脑网络的图形分析工具箱。
（18）BASCO：事件相关功能磁共振成像数据中的区域间功能连接分析。
（19）MNET：一款用于 fMRI 和 DTI 的全自动一体化网络分析工具箱。
（20）EEGNET：用于分析和可视化 M/EEG 连接的工具箱。
（21）BRAPH：使用图论进行大脑分析。
（22）FastFC：功能性大脑网络的高效计算。

5 思考

（1）模块化结构、具有hub结构以及具有小世界特征的网络结构都可以被归类为路由协议系列的通信模型，因为它们都采用高效、选择性的少量路径来传递信号，并且具有明确的特定性质和策略。因为，在路由协议中，信号是通过高效、选择性访问的少量路径传递的，这与模块化结构中的网络节点之间具有明确的模块化特征相符合。小世界网络是一种特殊的网络拓扑结构，具有高度集聚性和短平均路径长度的特征。具有hub结构的网络通常具有枢纽节点或中心节点，这些节点在整个网络中起到关键的连接作用，类似于路由协议中描述的高效路径。
（2）本文非常系统的讲解了当前脑网络通信的模型分类、每种模型的原理和优缺点，以及举了一些例子说明了脑网络通信对于实际研究有哪些应用。这些算法模型在Brain Connectivity Toolbox中都有实现，对于脑网络的研究实践提供了明确的指导。

这篇关于【博士每天一篇文献-综述】Brain network communication_ concepts, models and applications的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---