Unity URP 如何写基础的几何着色器

本文主要是介绍Unity URP 如何写基础的几何着色器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这是使用几何着色器在点中心生成一个点并根据这个点把原本的面片分成三个三角形的操作。

对于几何着色器构造相对简单，网上的信息也相对较多，需要注意的点就是需要提供一个新的数据结构供几何着色器输出，因为几何着色器在顶点之后，片元之前，所以结构体就需要模型输入的结构体、顶点输出的结构体、几何输出的结构体。

下面是完整代码

Shader "Kerzh/GeoShaderTest"
{Properties{_Length("Length",Float) = 1}SubShader{Tags {"LightMode" = "UniversalForward"}LOD 100Pass{Cull OffCGPROGRAM#pragma vertex vert#pragma fragment frag#pragma geometry geom#include "UnityCG.cginc"//cpu 传到 vsstruct appdata{float4 posOS : POSITION;float2 uv : TEXCOORD0;float4 normalOS : NORMAL;};//vs 传到 gsstruct v2g{float4 posOS    : TEXCOORD0;float2 uv       : TEXCOORD1;float3 normalOS : TEXCOORD2;};//gs 传到 fsstruct g2f{float4 posCS    : SV_POSITION;float2 uv       : TEXCOORD0;float3 normalWS : TEXCOORD1;float3 posWS    : TEXCOORD2;float  dis      : TEXCOORD3;};float _Length;v2g vert (appdata input){v2g output;output.uv = input.uv;output.normalOS = input.normalOS;output.posOS = input.posOS;return output;}//最大的顶点数，这里比如你要生成三个三角形面片，那么一个面片需要三个顶点，就是9个顶点[maxvertexcount(9)]void geom (triangle v2g input[3],inout TriangleStream<g2f> triStream){g2f center;  //  中间那个点center.uv = (input[0].uv + input[1].uv + input[2].uv)/3.0;//  计算中间点的uvfloat3 centerNormalOS = (input[0].normalOS + input[1].normalOS + input[2].normalOS)/3.0;center.normalWS = UnityObjectToWorldNormal(centerNormalOS );//  计算中间点的法线float3 centerPosOS = (input[0].posOS + input[1].posOS + input[2].posOS)/3.0;//  计算中间点的位置centerPosOS = centerPosOS + centerNormalOS *_Length;//  沿着中心点法线根据噪声及系数位移中心点//中心点后期所需数据center.posWS = mul(unity_ObjectToWorld, centerPosOS);center.posCS = UnityObjectToClipPos(centerPosOS);center.dis = 1;g2f output[3];  //  这里是原样把输入三角形的三个点放到了这里面，只是为了下面取得方便for(int i=0;i<3;i++){g2f p0;p0.uv = input[i].uv;p0.normalWS = UnityObjectToWorldNormal( input[i].normalOS);p0.posWS = mul(unity_ObjectToWorld, input[i].posOS);p0.posCS = UnityObjectToClipPos(input[i].posOS );p0.dis = 0;output[i] = p0;}//  根据这三个点分别和中心点制造三角形输出triStream.RestartStrip(); //  重新开始一个新的三角形triStream.Append(output[1]);triStream.Append(center);triStream.Append(output[0]);triStream.RestartStrip();  //  重新开始一个新的三角形triStream.Append(output[2]);triStream.Append(center);triStream.Append(output[1]);triStream.RestartStrip(); //  重新开始一个新的三角形triStream.Append(output[0]);triStream.Append(center);triStream.Append(output[2]);}float4 frag (g2f i) : SV_Target{return i.dis;return float4(i.uv,0,0);}ENDCG}}
}

关于其中几何着色器的部分

//最大的顶点数，这里比如你要生成三个三角形面片，那么一个面片需要三个顶点，就是9个顶点[maxvertexcount(9)]void geom (triangle v2g input[3],inout TriangleStream<g2f> triStream){g2f center;  //  中间那个点center.uv = (input[0].uv + input[1].uv + input[2].uv)/3.0;//  计算中间点的uvfloat3 centerNormalOS = (input[0].normalOS + input[1].normalOS + input[2].normalOS)/3.0;center.normalWS = UnityObjectToWorldNormal(centerNormalOS );//  计算中间点的法线float3 centerPosOS = (input[0].posOS + input[1].posOS + input[2].posOS)/3.0;//  计算中间点的位置centerPosOS = centerPosOS + centerNormalOS *_Length;//  沿着中心点法线根据噪声及系数位移中心点//中心点后期所需数据center.posWS = mul(unity_ObjectToWorld, centerPosOS);center.posCS = UnityObjectToClipPos(centerPosOS);center.dis = 1;g2f output[3];  //  这里是原样把输入三角形的三个点放到了这里面，只是为了下面取得方便for(int i=0;i<3;i++){g2f p0;p0.uv = input[i].uv;p0.normalWS = UnityObjectToWorldNormal( input[i].normalOS);p0.posWS = mul(unity_ObjectToWorld, input[i].posOS);p0.posCS = UnityObjectToClipPos(input[i].posOS );p0.dis = 0;output[i] = p0;}//  根据这三个点分别和中心点制造三角形输出triStream.RestartStrip(); //  重新开始一个新的三角形triStream.Append(output[1]);triStream.Append(center);triStream.Append(output[0]);triStream.RestartStrip();  //  重新开始一个新的三角形triStream.Append(output[2]);triStream.Append(center);triStream.Append(output[1]);triStream.RestartStrip(); //  重新开始一个新的三角形triStream.Append(output[0]);triStream.Append(center);triStream.Append(output[2]);}

大部分在注释中描述的相对明确，但要注意这些操作

center.uv = (input[0].uv + input[1].uv + input[2].uv)/3.0;//  计算中间点的uv
center.normalWS = UnityObjectToWorldNormal(centerNormalOS );//  计算中间点的法线
//中心点后期所需数据
center.posWS = mul(unity_ObjectToWorld, centerPosOS);
center.posCS = UnityObjectToClipPos(centerPosOS);
center.dis = noise;

根据一定的计算规则，给中心点赋予详细的顶点信息，这样他就和模型上初始存在的顶点无异，数据填充完毕后和原顶点一起组成片元，组成一个片元的操作如下。

triStream.RestartStrip(); //  重新开始一个新的三角形
triStream.Append(output[1]);
triStream.Append(center);
triStream.Append(output[0]);

通过这样的操作确立一个三角形片元中的三个点。

而这些点在像素着色器中调用时，因为是对每个像素调用，所以会根据这些点取插值，

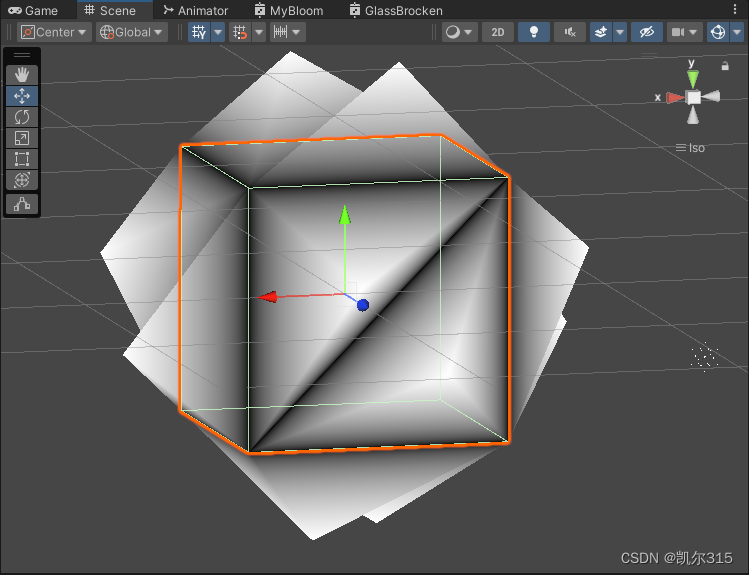
 这里的像素着色器是这么写的

float4 frag (g2f i) : SV_Target
{return i.dis;
}

所以对于一个片元中的像素，根据片元三个顶点的信息

struct g2f
{float4 posCS    : SV_POSITION;float2 uv       : TEXCOORD0;float3 normalWS : TEXCOORD1;float3 posWS    : TEXCOORD2;float  dis      : TEXCOORD3;
};

插值到对应像素，dis也就会呈现出一种渐变感。

这篇关于Unity URP 如何写基础的几何着色器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---