【数据挖掘】袋装、AdaBoost、随机森林算法的讲解及分类实战（超详细 附源码）

需要源码请点赞关注收藏后评论区留言私信~~~

组合分类

组合分类器（Ensemble）是一个复合模型，由多个分类器组合而成。组合分类器往往比它的成员分类器更准确

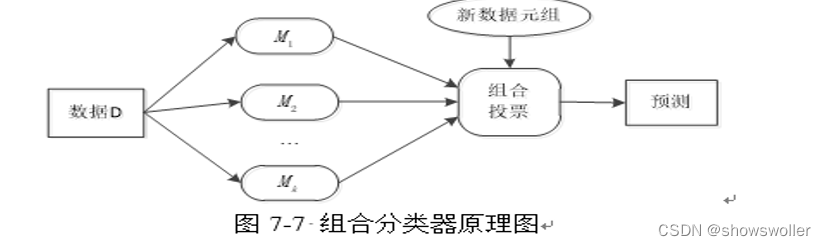
俗话说得好 三个臭皮匠顶过一个诸葛亮 此处也是如下

 1：袋装

袋装（Bagging）是一种采用随机有放回的抽样选择训练数据构造分类器进行组合的方法。如同找医生看病，选择多个医生，根据多个医生的诊断结果做出最终结果（多数表决），每个医生具有相同的投票权重

袋装分类器的准确率通常显著高于从原训练集D导出的单个分类器的准确率，即便有噪声数据和过拟合的影响，它的效果也不会很差，准确率的提高是因为符合摩西你个降低了个体分类器的方差

算法流程图如下

 在sklearn中，Bagging方法由BaggingClassifier统一提供，以用户输入的基模型和划分子集的方法作为参数。其中，max_samples和max_features控制子集的大小，而bootstrap和bootstrap_features控制数据样本和属性是否替换。Oob_score=True可使得估计时采用已有的数据划分样本

2：提升和AdaBoost

考虑找医生看病的另外一种情况，选择多个医生，根据多个医生的诊断结果做出最终结果（加权表决），每个医生具有不同的投票权重。这就是提升（Boosting）的基本思想

该算法流程图如下

scikit-learn中Adaboost类库包括AdaBoostClassifier和AdaBoostRegressor两个，AdaBoostClassifier用于分类，AdaBoostRegressor用于回归 

AdaBoostClassifier的使用

效果如下 可以大致分为两类

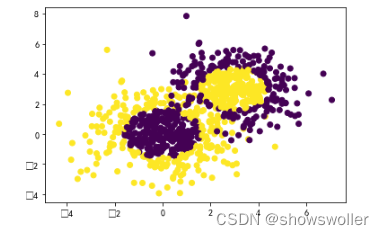
代码如下

# 生成2维正态分布，生成的数据按分位数分为两类，500个样本,2个样本特征，协方差系数为2
X1, y1 = make_gaussian_quantiles(cov=2.0,n_samples=500, n_features=2,n_classes=2, random_state=1)
# 生成2维正态分布，生成的数据按分位数分为两类，400个样本,2个样本特征均值都为3，协方差系数为2
X2, y2 = make_gaussian_quantiles(mean=(3, 3), cov=1.5,n_samples=400, n_features=2, n_classes=2, random_state=1)
#将两组数据合成一组数据
X = np.concatenate((X1, X2))
y = np.concatenate((y1, - y2 + 1))
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)

基于决策树的Adaboost来做分类拟合

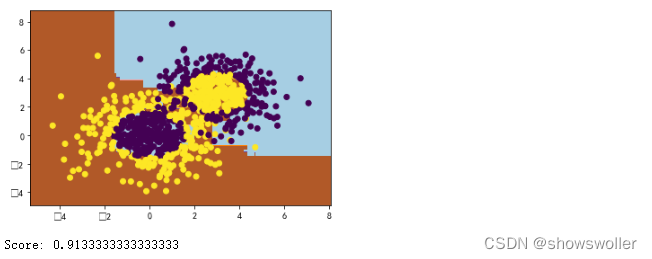
代码如下

bdt = AdaBoostClassifier(DecisionTreeClassifier(max_depth=2, min_samples_split=20, min_samples_leaf=5), algorithm="SAMME", n_estimators=200, learning_rate=0.8)
bdt.fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))
Z = bdt.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
cs = plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.show()
print('Score:', bdt.score(X,y))

 3：随机森林

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树。想象组合分类器中的每个分类器都是一棵决策树，因此分类器的集合就是一个“森林”。更准确说，每一棵树都依赖于独立抽样，并与森林中所有树具有相同分布的随机向量值。随机森林是利用多个决策树对样本进行训练、分类并预测的一种算法，主要应用于回归和分类场景。在对数据进行分类的同时，还可以给出各个变量的重要性评分，评估各个变量在分类中所起的作用。分类时，每棵树都投票并且返回得票最多的类

算法流程如下

（1）训练总样本的个数为N，则单棵决策树从N个训练集中有放回的随机抽取N个作为此单棵树的训练样本

（2）令训练样例的输入特征的个数为M，m远远小于M，则我们在每棵决策树的每个结点上进行分裂时，从M个输入特征里随机选择m个输入特征，然后从这m个输入特征里选择一个最好的进行分裂。m在构建决策树的过程中不会改变

（3）每棵树都一直这样分裂下去，直到该结点的所有训练样例都属于同一类，不需要剪枝

2. 随机森林的两种形式

（1）Forest-RI：使用装袋算法与随机属性选择结合构建。给定d个元组的训练集D，为组合分类器产生k棵决策树的一般过程如下：对于每次迭代i（i = 1,2,3,…，k），使用有放回的抽样，由D产生d个元组的训练集Di。也就是说，每个Di都是D的一个自助样本，使得某些元组可能在Di出现多次，而另一些可能不出现。设F是用来在每个结点决定划分的属性数，其中F远小于可用的属性数。为了构造决策树分类器Mi，在每个结点随机选择F个属性作为结点划分的候选属性。使用CART算法的方法来增长树。树增长达最大规模，并且不剪枝

（2）Forest-RC：使用输入属性的随机线性组合。它不是随机的选择一个属性子集，而是由已有属性的线性组合创建一些新属性（特征）。即一个属性由指定的L个原属性组合产生。在每个给定的结点，随机选取L个属性，并且从[-1,1]中随机选取的数作为系数相加。产生F个线性组合，并且其中搜索到最佳划分。当只有少量属性可用时，为了降低个体分类器之间的相关性，这种形式的随机森林是有用的

随机森林有诸多的优点  主要体现为以下几个方面

1：可以用来解决分类和回归问题 随机森林可以同时处理分类和数值特征

2：抗过拟合能力 通过平均决策树 降低过拟合的风险性

3：只有在半数以上的基分类器出现差错时才会做出错误的预测

4：对数据集的适应能力强：既能处理离散型数据 也能处理连续型数据 数据集无须规范化

5：由于随机森林在每次划分时只考虑很少的属性 因此它们在大型数据库上非常有效 可能比袋装和提升更快

随机森林Python实现

 结果如下 可以看出随机森林的精度明显比单颗决策树高

代码如下

from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
wine = load_wine()    #导入数据集
#划分训练集和测试集
from sklearn.model_selection import train_test_split
Xtrain, Xtest, Ytrain, Ytest = train_test_split(wine.data, wine.target, test_size = 0.3)
clf = DecisionTreeClassifier(random_state=0)
rfc = RandomFo, Ytrain)
rfc = rfc.fit(Xtrain, Ytrain)
#显示决策树和随机森林的准确率
score_c = clf.score(Xtest, Ytest)
score_r = rfc.score(Xtest, Ytest)
print("Single Tree: {} \n".format(score_c),"Random Forest: {}".format(score_r))

创作不易 觉得有帮助请点赞关注收藏~~~