惯性导航 | 航迹推算与gazebo仿真

本文主要是介绍惯性导航 | 航迹推算与gazebo仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

IMU数据进行短时间航迹推算

代码

声明一个用与 IMU积分的类 ，来实现 短时间内的航迹推算

类的名字叫 IMUIntegration
构造函数 有三个变量进行私有变量初始化 重力、初始陀螺仪零偏、初始加速度零偏。

class IMUIntegration {public:IMUIntegration(const Vec3d& gravity, const Vec3d& init_bg, const Vec3d& init_ba): gravity_(gravity), bg_(init_bg), ba_(init_ba) {}

下面是在imu数据一帧一帧进来，如何实现状态的积分，在使用的时候则是来一帧IMU数据，调用一次这个函数
函数名称

void AddIMU(const IMU& imu) {

计算时间间隔，与上一帧IMU数据时间间隔

double dt = imu.timestamp_ - timestamp_;

时间间隔满足要求，间隔时间不能过长

if (dt > 0 && dt < 0.1) {

更新位置，用上一帧的速度与姿态

p_ = p_ + v_ * dt + 0.5 * gravity_ * dt * dt + 0.5 * (R_ * (imu.acce_ - ba_)) * dt * dt;

对应公式：
$$p_j=p_k+\sum _{k=i}^{j-1}[v_k△t+\frac{1}{2}g△t^2]+\frac{1}{2}\sum _{k=i}^{j-1}{R}_k(\tilde{a}-b_{a,k})△t^2$$

更新速度，用上一帧的姿态

v_ = v_ + R_ * (imu.acce_ - ba_) * dt + gravity_ * dt;

对应公式：
$$v_j=v_k+\sum _{k=i}^{j-1}[R_k(\tilde{a}-b_{a,k})△t+g△t]$$

更新姿态（旋转矩阵）

R_ = R_ * Sophus::SO3d::exp((imu.gyro_ - bg_) * dt);

$$R_j=R_i\prod _{k=i}^{j-1}\exp ((\tilde{\omega }-b_{g,k})△t)$$

更新时间，用于判断下一帧数据，在时间间隔上是否满足要求

timestamp_ = imu.timestamp_;

返回有IMU积分的各个航迹状态

    /// 组成NavStateNavStated GetNavState() const { return NavStated(timestamp_, R_, p_, v_, bg_, ba_); }SO3 GetR() const { return R_; }Vec3d GetV() const { return v_; }Vec3d GetP() const { return p_; }

下面是私有变量的声明

   private:// 累计量SO3 R_;Vec3d v_ = Vec3d::Zero();Vec3d p_ = Vec3d::Zero();double timestamp_ = 0.0;// 零偏，由外部设定Vec3d bg_ = Vec3d::Zero();Vec3d ba_ = Vec3d::Zero();Vec3d gravity_ = Vec3d(0, 0, -9.8);  // 重力

gazebo中进行仿真测试

在gazebo中的IMU插件对惯导的噪声描述很简单，仅有一个高斯噪声可以设置。
其中xacro设置的一个例子如下：

     <gazebo reference="imu_base_link"><gravity>true</gravity><sensor name="imu_sensor" type="imu"><always_on>true</always_on><update_rate>200</update_rate><visualize>true</visualize><topic>/jk/imu</topic><plugin filename="libgazebo_ros_imu_sensor.so" name="imu_plugin"><topicName>/jk/imu</topicName>         <bodyName>imu_base_link</bodyName><updateRateHZ>200.0</updateRateHZ>    <gaussianNoise>0.00329</gaussianNoise>   <xyzOffset>0 0 0</xyzOffset>     <rpyOffset>0 0 0</rpyOffset><frameName>imu_base_link</frameName>        </plugin><pose>0 0 0 0 0 0</pose></sensor></gazebo>

其中gaussianNoise噪声参数 可以进行手动设置。

与真实的IMU 噪声模型差别很大，用rotors的imu插件，可以尽可能模拟IMU噪声模型

    <gazebo><plugin filename="librotors_gazebo_imu_plugin.so" name="rotors_gazebo_imu${imu_suffix}_plugin"><robotNamespace>${namespace}</robotNamespace> <!-- (string, required): ros namespace in which the messages are published --><linkName>${namespace}/imu${imu_suffix}_link</linkName> <!-- (string, required): name of the body which holds the IMU sensor --><imuTopic>${imu_topic}</imuTopic> <!-- (string): name of the sensor output topic and prefix of service names (defaults to imu) --><gyroscopeNoiseDensity>${gyroscope_noise_density}</gyroscopeNoiseDensity> <!-- Gyroscope noise density (two-sided spectrum) [rad/s/sqrt(Hz)] --><gyroscopeRandomWalk>${gyroscope_random_walk}</gyroscopeRandomWalk> <!-- Gyroscope bias random walk [rad/s/s/sqrt(Hz)] --><gyroscopeBiasCorrelationTime>${gyroscope_bias_correlation_time}</gyroscopeBiasCorrelationTime> <!-- Gyroscope bias correlation time constant [s] --><gyroscopeTurnOnBiasSigma>${gyroscope_turn_on_bias_sigma}</gyroscopeTurnOnBiasSigma> <!-- Gyroscope turn on bias standard deviation [rad/s] --><accelerometerNoiseDensity>${accelerometer_noise_density}</accelerometerNoiseDensity> <!-- Accelerometer noise density (two-sided spectrum) [m/s^2/sqrt(Hz)] --><accelerometerRandomWalk>${accelerometer_random_walk}</accelerometerRandomWalk> <!-- Accelerometer bias random walk. [m/s^2/s/sqrt(Hz)] --><accelerometerBiasCorrelationTime>${accelerometer_bias_correlation_time}</accelerometerBiasCorrelationTime> <!-- Accelerometer bias correlation time constant [s] --><accelerometerTurnOnBiasSigma>${accelerometer_turn_on_bias_sigma}</accelerometerTurnOnBiasSigma> <!-- Accelerometer turn on bias standard deviation [m/s^2] --></plugin></gazebo>

其中关键参数包括：

• accelerometer/gyroscopeNoiseDensity 测量噪声
• accelerometer/gyroscope_random_walk 随机游走

其中发布出来的一包数据如下：

header:
seq: 128
stamp:
secs: 22
nsecs: 290000000
frame_id: “imu_base_link”
orientation:
x: 0.0016563453004138674
y: -0.0008542007888005784
z: 0.006514394955332766
w: 1.001055072733733
orientation_covariance: [1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05]
angular_velocity:
x: 0.0014246123123964744
y: 0.0027524592879204523
z: 0.0007163285834896606
angular_velocity_covariance: [1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05]
linear_acceleration:
x: -0.0029448312010755674
y: -0.00014593761997295991
z: 9.795575703789861
linear_acceleration_covariance: [1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05, 0.0, 0.0, 0.0, 1.08241e-05]

自定义的IMU数据结构体如下：

struct IMU {IMU() = default;IMU(double t, const Vec3d& gyro, const Vec3d& acce) : timestamp_(t), gyro_(gyro), acce_(acce) {}double timestamp_ = 0.0;Vec3d gyro_ = Vec3d::Zero();Vec3d acce_ = Vec3d::Zero();
};

所以需要在IMU的回调函数里面，赋值上面的结构体数据

        sad::IMU imu;imu.timestamp_ = Imu_msg->header.stamp.toSec();imu.gyro_ << Imu_msg->angular_velocity.x,Imu_msg->angular_velocity.y,Imu_msg->angular_velocity.z;imu.acce_ << Imu_msg->linear_acceleration.x,Imu_msg->linear_acceleration.y,Imu_msg->linear_acceleration.z;

然后将数据加入，在该函数内部，即完成航迹的推算

AddIMU(imu);

发布一个里程计数据，来查看航迹推算的结果

        nav_msgs::Odometry imu_Integration_Odom;//声明一个里程计 来记录推算的结果imu_Integration_Odom.header = Imu_msg->header;imu_Integration_Odom.pose.pose.position.x = p_[0];imu_Integration_Odom.pose.pose.position.y = p_[1];imu_Integration_Odom.pose.pose.position.z = p_[2];imu_Integration_Odom.twist.twist.linear.x = v_[0];imu_Integration_Odom.twist.twist.linear.y = v_[1];imu_Integration_Odom.twist.twist.linear.z = v_[2];

将旋转矩阵转成欧拉角单位为度，方便直观查看

        float yaw = atan2(R_.matrix()(1,0), R_.matrix()(0,0));  float roll = atan2(R_.matrix()(2,1), R_.matrix()(2,2));float pitch = atan2(-R_.matrix()(2,0), sqrt(R_.matrix()(0,0) * R_.matrix()(0,0) + R_.matrix()(1,0) * R_.matrix()(1,0)));imu_Integration_Odom.pose.pose.orientation.x = pitch/0.01745329252;imu_Integration_Odom.pose.pose.orientation.y = roll/0.01745329252;imu_Integration_Odom.pose.pose.orientation.z = yaw/0.01745329252;

发布里程计

imu_Integration_Odom_pub_.publish(imu_Integration_Odom);

无人机在地面静止不动情况下
曲线结果数据如下：

• 位置（很快就飘掉了）
  
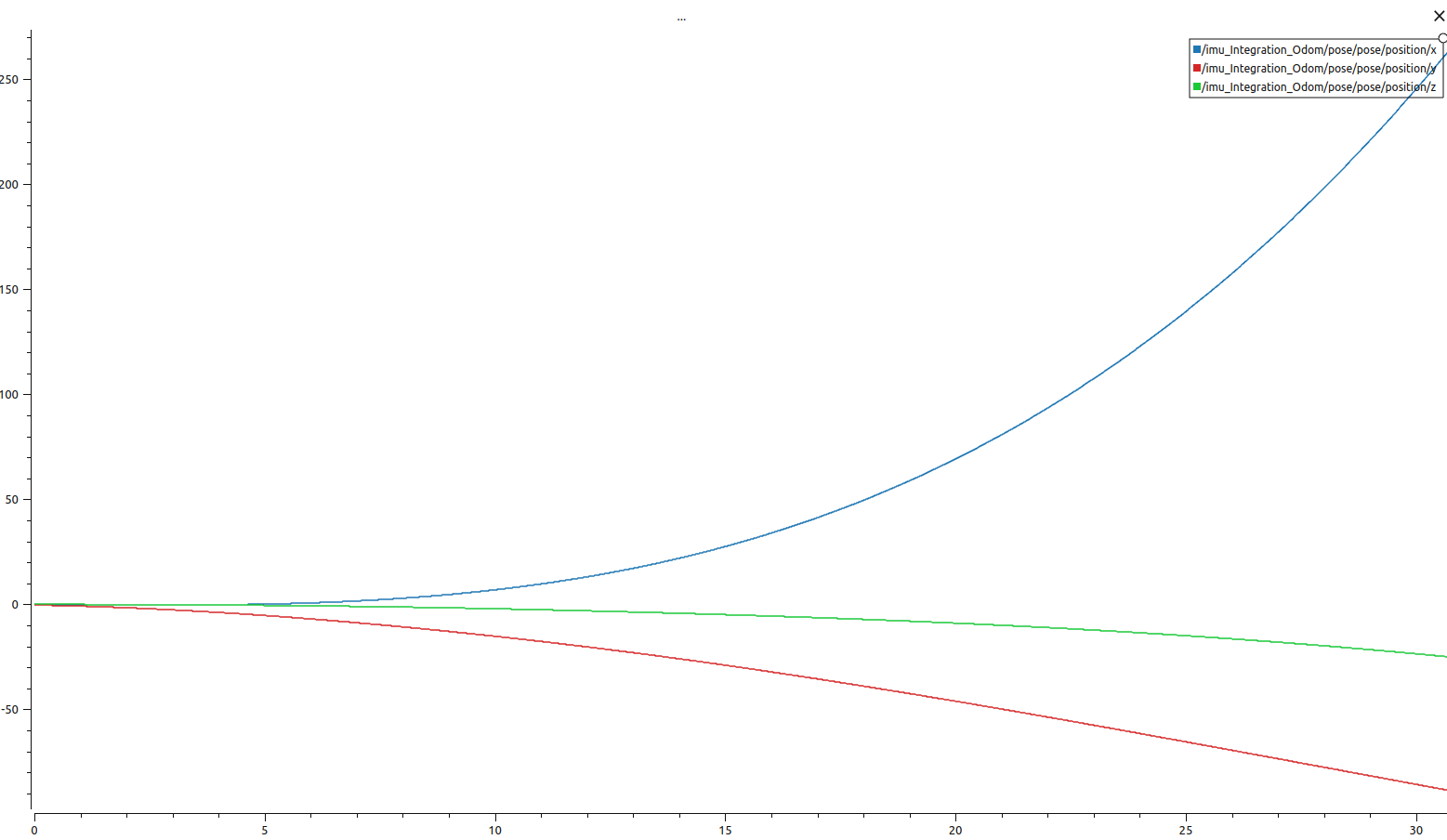
• 速度（与位置类似，越来越大）
  
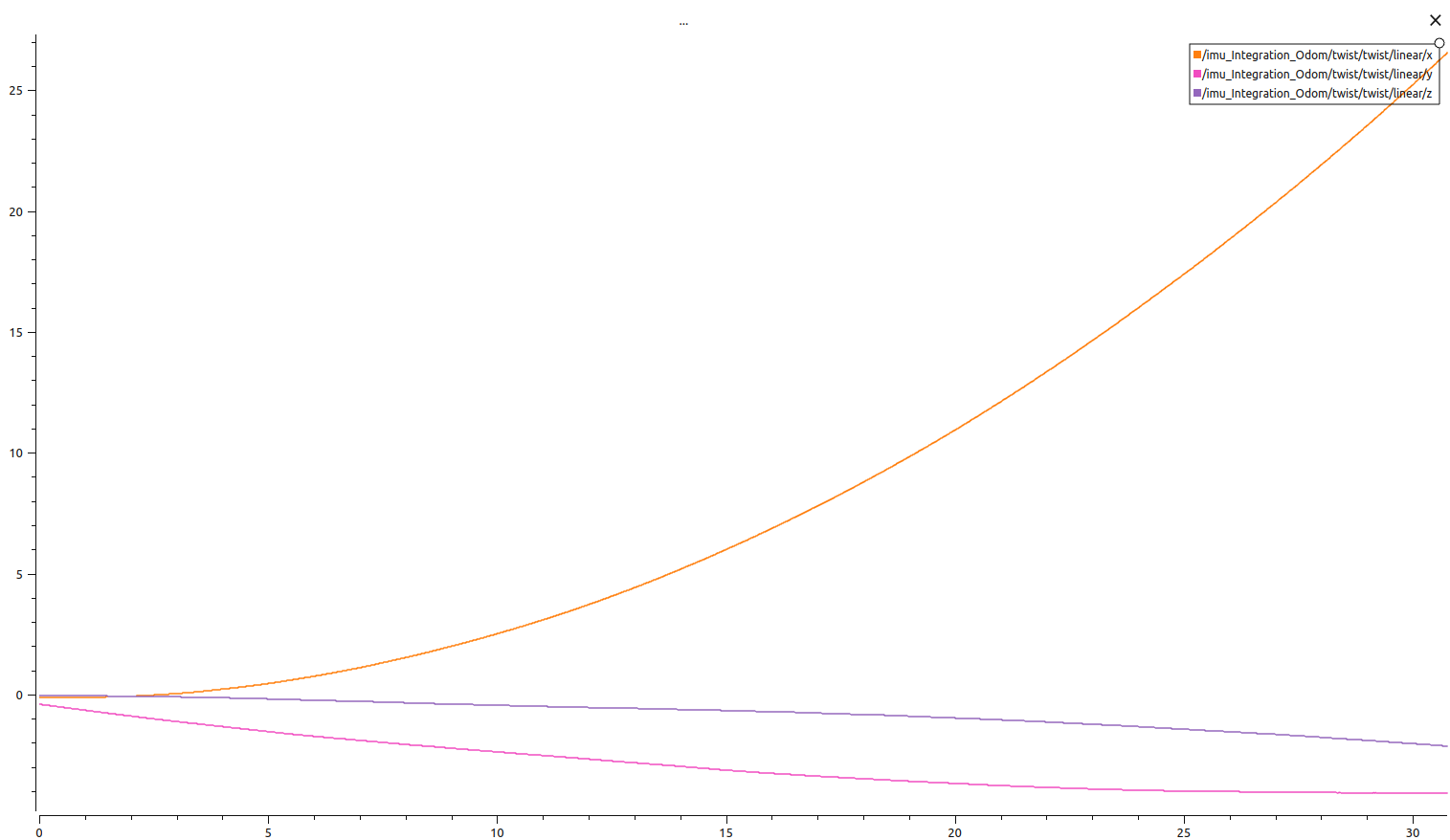
• 欧拉角度 （航向角度保持还可以）
  

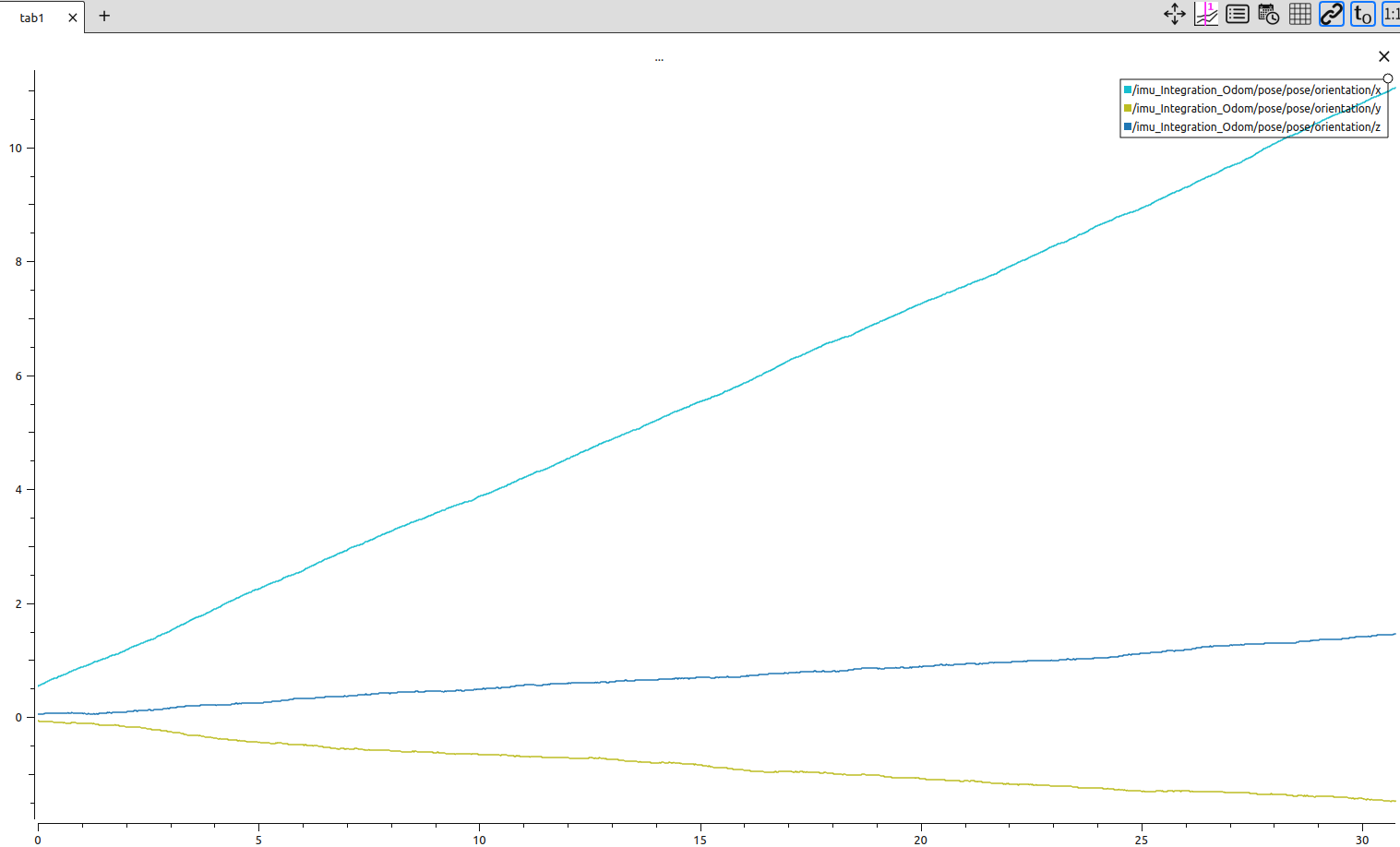
这篇关于惯性导航 | 航迹推算与gazebo仿真的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---