本文主要是介绍C#,最小代价多边形三角剖分MCPT(Minimum Cost Polygon Triangulation)算法与源代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 最小代价多边形三角剖分算法
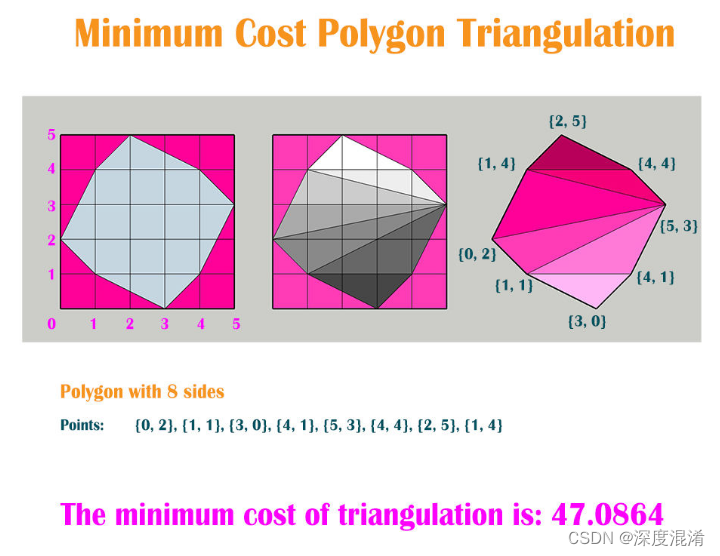
凸多边形的三角剖分是通过在非相邻顶点(角点)之间绘制对角线来形成的,这样对角线就不会相交。问题是如何以最小的代价找到三角剖分的代价。三角剖分的代价是其组成三角形的权重之和。每个三角形的重量是其周长(所有边的长度之和)
请参阅以下来源的示例。
多项式三角
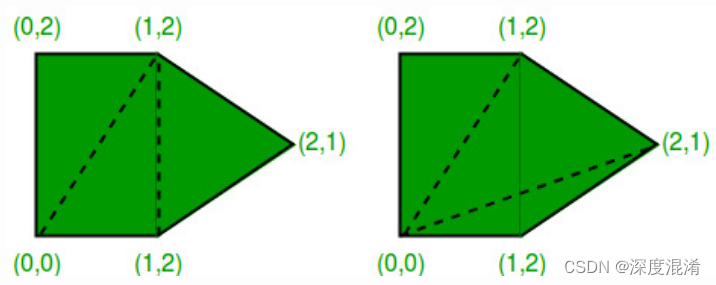
同一凸五边形的两个三角剖分。左侧的三角测量的成本为8+2√2+2√5(约15.30),右侧的成本为4+2√2 + 4√5(约15.77)。
建议:在继续解决方案之前,请先在{IDE}上尝试您的方法。
该问题具有递归子结构。其思想是将多边形分为三部分:单个三角形、左侧的子多边形和右侧的子多边形。我们尝试所有可能的分割,像这样,找到一个最小化三角形成本加上两个子多边形三角剖分成本的分割。
设顶点从i到j的三角剖分的最小代价为最小代价(i,j)
如果j<=i+2,则
最小成本(i,j)=0
其他的
最小成本(i,j)=最小{最小成本(i,k)+最小成本(k,j)+成本(i,k,j)}
这里k从“i+1”到“j-1”变化
由边(i,j)、(j,k)和(k,i)形成的三角形的成本为
成本(i,j,k)=距离(i,j)+距离(j,k)+距离(k,i)
2 源代码
using System;
using System.Collections;
using System.Collections.Generic;using Legalsoft.Truffer.TGraph;namespace Legalsoft.Truffer.Algorithm
{public static partial class Algorithm_Gallery{public static double MCPT_Solve(TPoint[] vertices, int i, int j){if (j < (i + 2)){return 0;}double cost = float.MaxValue;for (int k = i + 1; k <= j - 1; k++){double weight = vertices[i].Distance(vertices[j]) + vertices[j].Distance(vertices[k]) + vertices[k].Distance(vertices[i]);cost = Math.Min(cost, weight + MCPT_Solve(vertices, i, k) + MCPT_Solve(vertices, k, j));}return cost;}private static double MCPT_Cost(TPoint[] points, int i, int j, int k){TPoint p1 = points[i];TPoint p2 = points[j];TPoint p3 = points[k];return TPoint.Distance(p1, p2) + TPoint.Distance(p2, p3) + TPoint.Distance(p3, p1);}public static double MCPT_Solve(TPoint[] points, int n){if (n < 3){return 0;}double[,] table = new double[n, n];for (int gap = 0; gap < n; gap++){for (int i = 0, j = gap; j < n; i++, j++){if (j < i + 2){table[i, j] = 0.0;}else{table[i, j] = 1000000.0;for (int k = i + 1; k < j; k++){double val = table[i, k] + table[k, j] + MCPT_Cost(points, i, j, k);if (table[i, j] > val){table[i, j] = val;}}}}}return table[0, n - 1];}}
}
3 源程序
using System;
using System.Collections;
using System.Collections.Generic;
using Legalsoft.Truffer.TGraph;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Algorithm_Gallery
{
public static double MCPT_Solve(TPoint[] vertices, int i, int j)
{
if (j < (i + 2))
{
return 0;
}
double cost = float.MaxValue;
for (int k = i + 1; k <= j - 1; k++)
{
double weight = vertices[i].Distance(vertices[j]) + vertices[j].Distance(vertices[k]) + vertices[k].Distance(vertices[i]);
cost = Math.Min(cost, weight + MCPT_Solve(vertices, i, k) + MCPT_Solve(vertices, k, j));
}
return cost;
}
private static double MCPT_Cost(TPoint[] points, int i, int j, int k)
{
TPoint p1 = points[i];
TPoint p2 = points[j];
TPoint p3 = points[k];
return TPoint.Distance(p1, p2) + TPoint.Distance(p2, p3) + TPoint.Distance(p3, p1);
}
public static double MCPT_Solve(TPoint[] points, int n)
{
if (n < 3)
{
return 0;
}
double[,] table = new double[n, n];
for (int gap = 0; gap < n; gap++)
{
for (int i = 0, j = gap; j < n; i++, j++)
{
if (j < i + 2)
{
table[i, j] = 0.0;
}
else
{
table[i, j] = 1000000.0;
for (int k = i + 1; k < j; k++)
{
double val = table[i, k] + table[k, j] + MCPT_Cost(points, i, j, k);
if (table[i, j] > val)
{
table[i, j] = val;
}
}
}
}
}
return table[0, n - 1];
}
}
}
这篇关于C#,最小代价多边形三角剖分MCPT(Minimum Cost Polygon Triangulation)算法与源代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








